Teoremi di Thevenin e Norton con il principio di sovrapposizione

I teoremi di Thevenin e di Norton possono essere dimostrati con il principio di sovrapposizione degli effetti.

Dimostrazione del circuito di Thevenin

Devo dimostrare che un circuito lineare è equivalente al circuito di Thevenin.

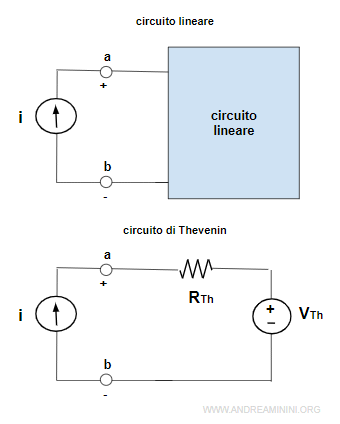
Per ipotesi, il circuito lineare è composto da un generatore di corrente esterno (i), due generatori indipendenti di corrente i₁ e i₂ e due generatori indipendenti di tensione v₁ e v₂.

Qualsiasi variabile del circuito, ad esempio la tensione ai terminali a-b, posso ottenerla con il principio di sovrapposizione.

Per il principio di sovrapposizione la tensione v è uguale a

$$ v = K_0 \cdot i + K_1 \cdot v_1 + K_2 \cdot v_2 + K_3 \cdot i_1 + K_4 \cdot i_2 $$

Dove K₀,K₁,K₂,K₃,K₄ sono costanti.

Ogni termine identifica il contributo del generatore indipendente, compreso il generatore esterno, alla tensione v del circuito.

Per semplificare l'analisi esprimo con la variabile G₀ il contributo dei generatori esterni.

$$ G_0 = K_1 \cdot v_1 + K_2 \cdot v_2 + K_3 \cdot i_1 + K_4 \cdot i_2 $$

In questo modo posso esprimere la formula della tensione in una forma più compatta

$$ v = K_0 \cdot i + G_0 $$

A questo punto devo trovare i valori delle costanti K₀ e G₀.

Per farlo ipotizzo varie situazioni:

A] Circuito aperto

Se il circuito è aperto nei terminali a-b si ha i=0.

$$ v = K_0 \cdot i + G_0 \:\:\: con \: i=0$$

$$ v = G_0 $$

La tensione è uguale al contributo dei generatori indipendenti G₀ che ha lo stesso valore V_Th della tensione di Thevenin.

$$ G_0 = V_{Th} $$

B] generatori spenti

Quando i generatori indipendenti sono spenti vale G₀=0

$$ v = K_0 \cdot i + G_0 \:\:\: con \: G_0=0$$

$$ v = K_0 \cdot i $$

In questo caso il termine K₀ è uguale alla resistenza equivalente di Thevenin R_Th

$$ K_0 = R_{Th} $$

C] In conclusione

Sostituendo i valori G₀=V_Th e K₀=R_Th nell'espressione

$$ v = K_0 \cdot i + G_0 $$

ottengo

$$ v = R_{Th} \cdot i + V_{Th} $$

che esprime la relazione tra la tensione e la corrente ai terminali a-b nel circuito di Thevenin.

Pertanto, i due circuiti sono equivalenti.

Dimostrazione del circuito di Norton

Ora provo a dimostrare che un circuito lineare è equivalente al circuito di Norton usando il principio di sovrapposizione.

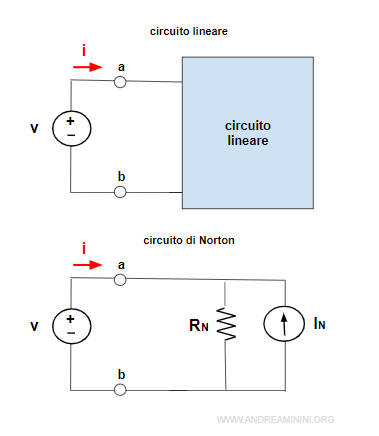
Utilizzo il principio di sovrapposizione per calcolare la corrente i del circuito lineare.

$$ i = K \cdot v + G $$

Dove K è il contributo del generatore di tensione v mentre G è il contributo dei generatori indipendenti interni al circuito lineare.

Per trovare K e G analizzo due situazioni

A] Cortocircuito a-b

Quando i terminali a-b sono in cortocircuito vale v=0.

$$ i = K \cdot v + G $$

$$ i = K \cdot 0 + G $$

$$ i = G $$

La corrente uscente dal nodo a nel cortocircuito è quella del generatore di Norton (i_N).

Quindi, la componente G vale -i_N.

$$ -i_N = G $$

B] Generatori spenti

Quando i generatori indipendenti sono spenti vale G=0.

$$ i = K \cdot v + G $$

$$ i = K \cdot v + 0 $$

$$ i = K \cdot v $$

$$ \frac{i}{v} = K $$

Quindi secondo la legge di Ohm K è uguale a una conduttanza che posso scrivere anche come resistenza equivalente R_N di Norton

$$ K = \frac{1}{R_N} $$

C] In conclusione

Sostituendo i valori G=-i_N e K=R_N nell'espressione

$$ i = K \cdot v + G $$

ottengo

$$ i = \frac{1}{R_N} \cdot v -i_N $$

$$ i = \frac{v}{R_N} -i_N $$

che esprime la relazione tra la tensione e la corrente ai terminali a-b nel circuito di Norton.

Pertanto, i due circuiti sono equivalenti.

E così via