Condizione di quasi stazionarietÓ
Cos'è la condizione di quasi stazionarietà
La condizione di quasi stazionarietà si verifica quando un circuito elettrico è molto più piccolo rispetto alla lunghezza d'onda del segnale elettrico.
In condizioni di quasi stazionarietà le variabili del sistema possono variare (non sono costanti) ma lo spazio massimo percorso da un segnale in un circuito elettrico è molto più piccolo rispetto alla lunghezza d’onda.
Pertanto, tutti i componenti di un circuito elettrico “vedono” lo stesso segnale elettrico nello stesso momento.
La spiegazione
Se il circuito è molto più piccolo della lunghezza d'onda, ogni parte del circuito "vede" lo stesso segnale.
Ad esempio, considero due punti di un circuito chiuso A e B.
Questi due punti distano Lmax metri.
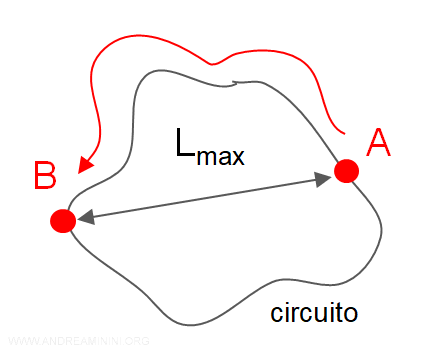
Se la lunghezza d'onda del segnale (λ) è molto più grande di Lmax, il ritardo del segnale tra la partenza e l'arrivo nei punti A e B è minimo.
Quando il segnale arriva al punto B è molto simile al segnale di partenza (A).
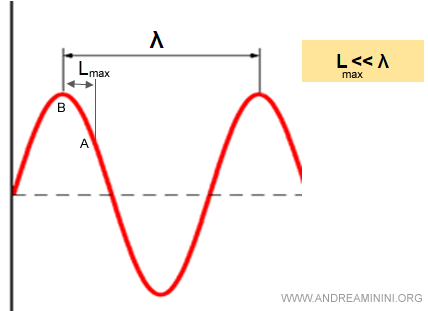
Pertanto, nello stesso istante di tempo il punto B vede all'incirca lo stesso segnale elettromagnetico del punto A.

Questo mi permette di studiare il circuito elettrico come se fosse in condizioni di stazionarietà, ossia con il campo elettrico e il campo magnetico costanti, anche se il segnale elettromagnetico è variabile.
A cosa serve la condizione di stazionarietà? La condizione di stazionarietà semplifica le equazioni di Maxwell che sono alla base di tutti i fenomeni elettromagnetici.
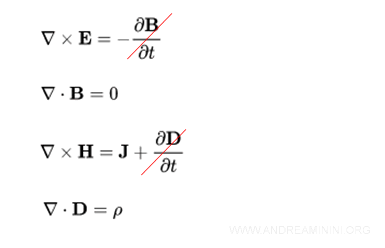
Grazie a questa semplificazione posso usare le leggi di Kirchhoff anche nei circuiti in cui la tensione e la corrente sono variabili. Senza la condizione di stazionarietà non sarebbero più valide.
In condizioni di quasi stazionarietà le leggi di Kirchhoff sono valide anche se i campi elettrici cambiano nel tempo.
Per soddisfare la condizione di quasi stazionarietà nel corso del tempo sono stati costruiti circuiti elettrici sempre più piccoli ( miniaturizzazione ).
A sua volta la miniaturizzazione ha permesso di aumentare progressivamente la frequenza dei segnali elettromagnetici.
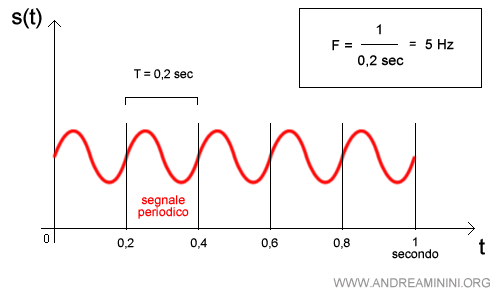
Cos’è la frequenza? La frequenza misura il numero di cicli completi che un’onda di lunghezza d’onda λ e periodo T compie un secondo. $$ f = \frac{1 \ s}{T} $$ Il periodo T è il tempo necessario per compiere un ciclo completo. Ad esempio, quest'onda compie cinque cicli in un secondo perché il suo periodo è T=0.2 sec. Quindi la frequenza del segnale è uguale a 5 Hz.
Perché la miniaturizzazione ha aumentato la frequenza dei circuiti?
Grazie alla miniaturizzazione le distanze in un circuito elettrico sono diventate sempre più piccole Lmax
Questo ha permesso di ridurre la lunghezza d’onde del segnale (λ) nel rispetto del principio di quasi stazionarietà.
Un segnale con minore lunghezza d'onda compie più cicli completi in un secondo. Quindi ha frequenza maggiore.
Grazie alla frequenza più alta il circuito trasmette ed elabora più informazioni in un secondo.
Ecco perché una CPU a 3 GHz è più veloce di una 2 GHz.
Nota. Negli ultimi decenni la miniaturizzazione dei circuiti ha permesso di costruire processori ad elevate frequenza (2-3 GHz) nei PC di ultima generazione. All'inizio degli anni '90 i processori avevano pochi MHz di frequenza. Erano mille volte più lenti.
La dimostrazione
Per analizzare il ritardo in un circuito devo considerare il ritardo massimo possibile 𝜏max
Il ritardo massimo possibile 𝜏max è il tempo necessario per spostarsi tra i due punti A e B più lontani del circuito che distano tra loro Lmax.

Sapendo che la velocità (V) in fisica è il rapporto tra lo spazio (S) e il tempo (T)
$$ V = \frac{S}{T} $$
Dove T= 𝜏max è il tempo di ritardo massimo che devo calcolare
$$ V = \frac{S}{\tau_{max}} $$
Lo spazio è invece S=Lmax la distanza tra i punti A e B ed è un dato noto.
$$ V = \frac{L_{max}}{\tau_{max}} $$
Anche la velocità V è un dato che conosco perché qualsiasi sengale elettromagnetico si sposta alla velocità della luce (c). Circa 299mila km/sec.
$$ c = \frac{L_{max}}{\tau_{max}} $$
Poiché conosco sia Lmax che c posso ricavare il ritardo massimo con un semplice passaggio algebrico
$$ \tau_{max} = \frac{L_{max}}{c} $$
Poiché la velocità della luce è una costante (c) ne consegue che l'unico modo per ridurre il ritardo massimo 𝜏max consiste nel ridurre le dimensioni del circuito (Lmax).
Quando invio un segnale elettromagnetico Im (es. un bit) dal punto A al punto B del circuito, in condizioni di non stazionarietà tra la partenza e l’arrivo si verifica un ritardo 𝜏
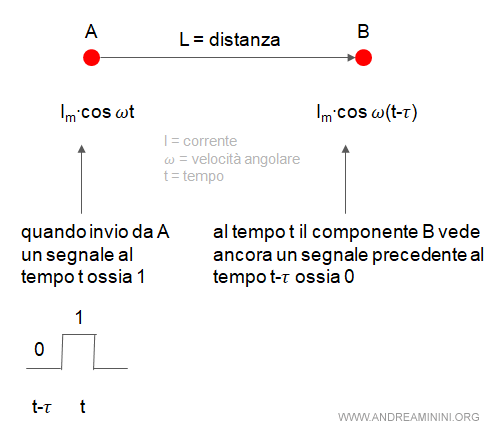
Se il ritardo è eccessivo al tempo t il componente B vede il segnale uguale a zero mentre il componente A vede il segnale uguale a uno.
In queste circostanze le leggi di Kirchhoff non sono applicabili.
Pertanto il ritardo massimo deve essere minimizzato facendo tendere a zero la componente ω𝜏.

Dove per 𝜏 intendo il ritardo massimo 𝜏max = Lmax/c
$$ \omega \tau = \omega \cdot \frac{L_{max}}{c} $$
Il termine ω è la velocità angolare del segnale sinusoidale ossia ω=2πf
$$ \omega \tau = (2 \pi \cdot f ) \cdot \frac{L_{max}}{c} $$
Sapendo che la frequenza (f) è l'inverso del periodo (T) del segnale sinusoidale ossia f=1/T
$$ \omega \tau = (2 \pi \cdot \frac{1}{T} ) \cdot \frac{L_{max}}{c} $$
Sapendo che la velocità è un rapporto spazio fratto tempo V=S/T dove S è la lunghezza d'onda λ e V=c è la velocità della luce ottengo T=S/V ossia T=λ/c
$$ \omega \tau = (2 \pi \cdot \frac{1}{\frac{λ}{c}} ) \cdot \frac{L_{max}}{c} $$
$$ \omega \tau = (2 \pi \cdot \frac{c}{λ} ) \cdot \frac{L_{max}}{c} $$
$$ \omega \tau = 2 \pi \cdot \frac{L_{max}}{λ} $$
Pertanto la componente ωt→0 tende a zero quando la lunghezza d'onda λ è molto più grande della grandezza del circuito Lmax
$$ \lambda >> L_{max} $$
E così via.
