Teorema di Norton

Secondo il teorema di Norton una rete lineare con due terminali a-b può essere sostituita da un circuito equivalente con un generatore di corrente i_N in parallelo a un resistore R_N.

Dove i_N è la corrente che scorre tra i terminali a-b messi in cortocircuito mentre R_N è il resistore equivalente quando i generatori indipendenti sono disattivati.

Come funziona

Divido un circuito in due sotttocircuiti separati tra loro mediante due nodi a-b.

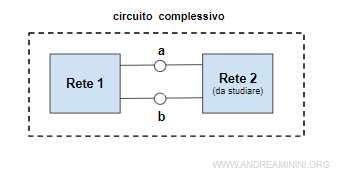
Il sottocircuito a destra dei nodi a-b è il circuito da studiare, detto carico (load).

Il sottocircuito a sinistra dei nodi a-b è un circuito lineare da semplificare tramite il teorema di Norton. Viene sostituito con una rete composta da un generatore di corrente e un resistore equivalente in parallelo.

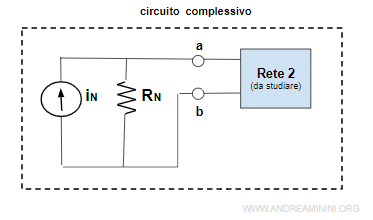
Nota. Due circuiti sono equivalenti se hanno la stessa relazione voltaggio/corrente ai terminali a-b. $$ i_{ab}=i_{N} $$

A cosa serve il teorema di Norton

E' utile per semplificare le parti non rilevanti di un circuito, sostituendole con un generatore di corrente e una resistenza equivalente, per concentrare l'analisi su un sottocircuito.

Come calcolare il circuito equivalente

Per determinare il circuito equivalente di Norton elimino temporaneamente la rete2 dal circuito complessivo.

In questo modo posso concentrarmi a semplificare la rete1.

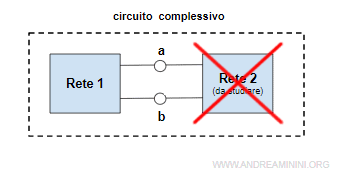
Poi calcolo la corrente i_N ai capi dei nodi a-b cortocircuitati e la resistenza equivalente R_N.

• Il generatore di corrente equivalente ha una corrente i_N pari alla corrente che scorre nel sottocircuito da semplificare tra i due nodi a-b messi in cortocircuito.
  

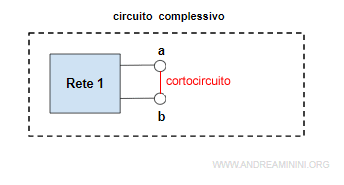
  Nota. Questo è normale perché il sottocircuito originale e semplificato devono essere equivalenti. Pertanto, la corrente ai morsetti a-b deve essere la stessa.

• Il resistore equivalente R_N si ottiene cortocircuitando i generatori di tensione indipendenti e aprendo i generatori indipendenti di corrente.
  
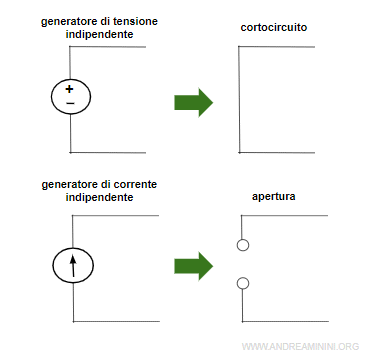
  I generatori dipendenti di tensione o corrente, invece, non devo spegnerli perché dipendono da altre variabili del circuito.
  

  Nota. Il resistore equivalente si calcola come nel teorema di Thevenin. Pertanto, c'è una stretta relazione tra i teoremi di Norton e Thevenin. $$ i_N = \frac{V_{Th}}{R_{Th}} $$

Un esempio pratico

In un circuito elettrico devo studiare la tensione v_o e la corrente i_o ai capi dell'elemento RL

Inserisco due nodi a-b per separare la parte del circuito che mi interessa dal resto del circuito.

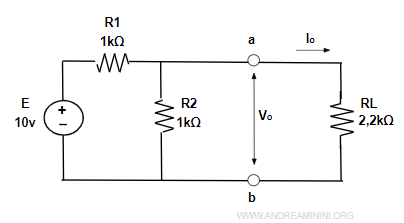
Il sottocircuito a destra dei morsetti a-b è il carico (load). E' quello che voglio studiare.

Il sottocircuito a sinistra di a-b è invece quello da semplificare.

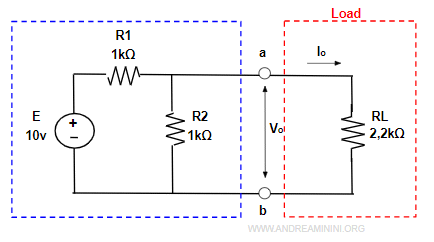
Applico il teorema di Norton per semplificare la parte sinistra (blu) del circuito elettrico.

La parte destra (rossa) posso ignorarla perché non devo modificarla. Quindi, la elimino temporaneamente.

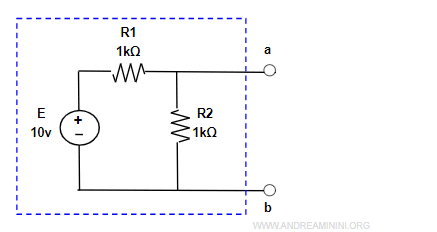
Metto in cortocircuito i terminali a-b.

In questo modo posso calcolare la corrente ai terminali a-b.

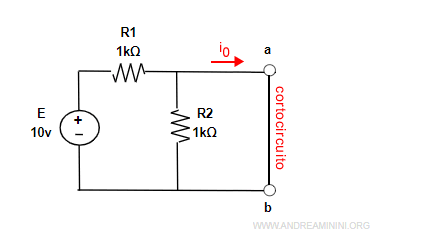
Posso ottenere la corrente i₀ tramite la legge di Ohm.

$$ i_0 = \frac{v}{R_1} = \frac{10}{1000} = 0,01 \: A = 10 \: mA $$

Ho trovato la corrente del generatore equivalente i_N

$$ i_N = 0,01 \: A $$

A questo punto devo calcolare il resistore equivalente R_N.

Metto in cortocircuito il generatore di tensione indipendente.

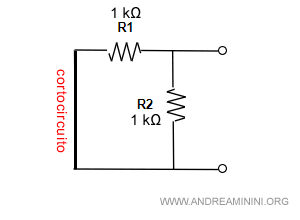
Poi applico una tensione da 1V in entrata sui morsetti a-b per calcolare il resistore equivalente.

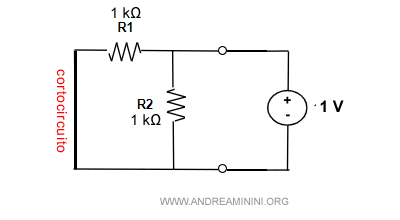
I resistori R1 e R2 sono in parallelo.

$$ R_1 \: || \: R_2 = \frac{R_1 \cdot R_2}{ R_1 + R_2 } $$

$$ R_1 \: || \: R_2 = \frac{1000 \cdot 1000}{ 1000 + 1000 } = 500 Ω $$

Pertanto, il resistore equivalente di Norton ha una resistenza di 500.

$$ R_N = 500Ω $$

Una volta trovati i valori del generatore di corrente i_N=0,01 A e del resistore R_N=500Ω, posso disegnare il circuito equivalente di Norton.

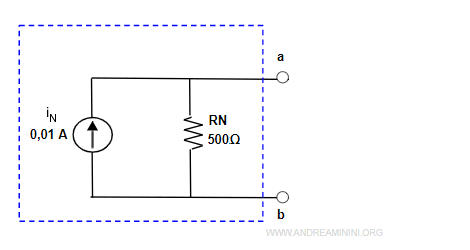
Il nuovo sottocircuito è equivalente al precedente perché ha la stessa tensione/corrente ai morsetti a-b ma è molto più semplice.

A questo punto riaggiungo il sottocircuito di destra (carico) per completare il circuito complessivo.

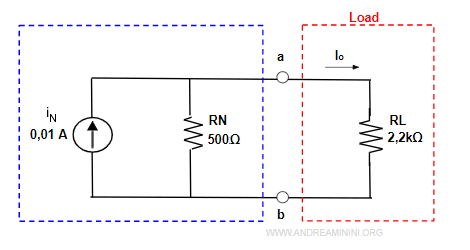
Anche il circuito complessivo è equivalente all'originale ma è decisamente più semplice da studiare.

E così via.