La trasformazione dei generatori di un circuito
La trasformazione dei generatori è un metodo di semplificazione del circuito. Ogni sorgente di tensione V in serie con un resistore R può essere sostituita con una sorgente di corrente in parallelo con il resistore, o viceversa, purché siano soddisfatte le seguenti regole $$ v = i \cdot R \\ \\ i = \frac{v}{R} $$
A cosa serve?
Si crea un circuito equivalente al circuito originale con le stesse caratteristiche.
Esempio
Questi dei circuiti sono equivalenti tra loro, perché ai terminali a-b hanno la stessa tensione e corrente.
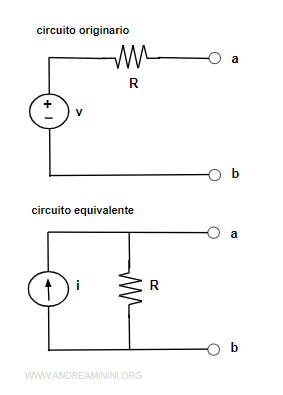
Pertanto, non modifica il resto del circuito.
Nota. La trasformazione può essere applicata sia alle sorgenti dipendenti che indipendenti di tensione o corrente.
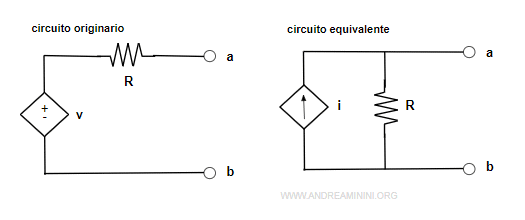
Un esempio pratico
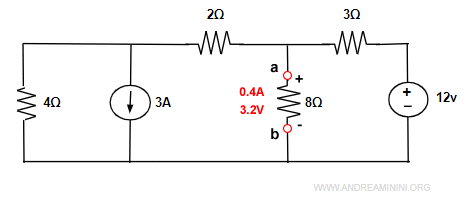
Provo a semplificare questo circuito tramite la trasformazione dei generatori.
Voglio calcolare la tensione e la corrente ai terminali a e b.
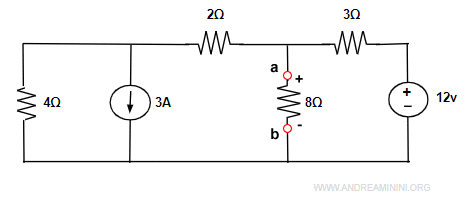
Posso trasformare la prima maglia a sinistra sostituendo il generatore continuo di corrente (3A) e resistore in parallelo (4Ω)
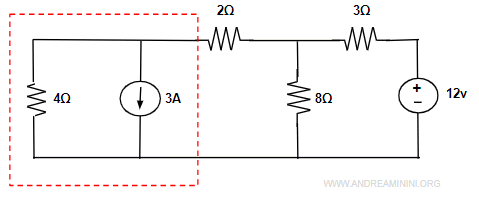
con un generatore continuo di tensione (12v) e un resistore in serie (4Ω).
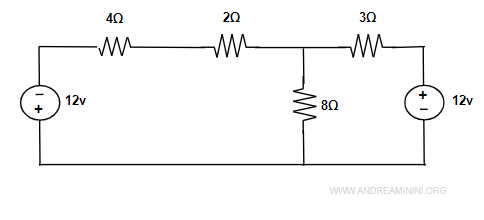
Nota. La tensione del generatore è 12 v per effetto della legge di Ohm (v=iR). Nella maglia la corrente è i=3A e la resistenza R=4Ω. Pertanto, la tensione è v=3·4=12 v.
Questa trasformazione mi permette di ottenere due resistenze in serie
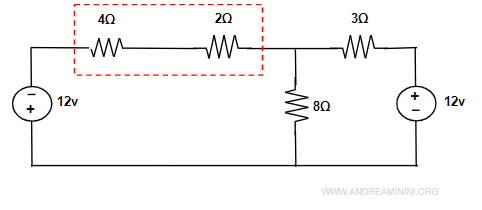
che posso semplificare con la somma delle due resistenze 4Ω+2Ω = 6Ω
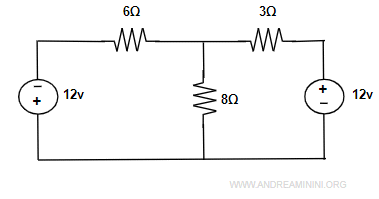
A questo punto trasformo la maglia con il generatore di tensione (12v) e la resistenza in serie (6Ω).
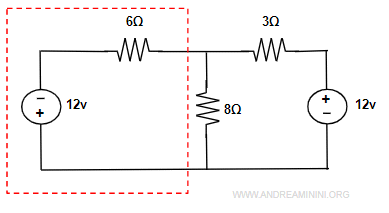
con un generatore di corrente da 2A e un resistore in parallelo da 6Ω.
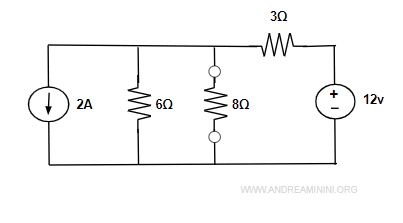
Nota. Il generatore di corrente è da 2A per effetto della legge di Ohm (v=iR) applicata alla maglia. In questo caso v=12 e R=6. Pertanto i=v/R=12/6=2 A.
Trasformo la maglia a destra con il generatore di tensione (12v) e la resistenza in serie (3Ω)
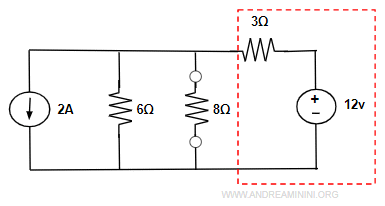
in un generatore di corrente (4A) e un resistore in serie (3Ω).
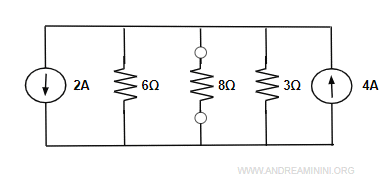
Nota. Il generatore di corrente è da 4A per effetto della legge di Ohm (v=iR) applicata alla maglia. In questo caso v=12 e R=3. Pertanto i=v/R=12/3=4 A.
Questo mi permette di ottenere un circuito equivalente con tre resistori in parallelo.
Il resistore da 8Ω non lo considero perché è quello di cui devo calcolare tensione e corrente.
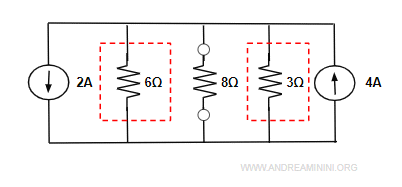
Gli altri due resistori in parallelo posso sostituirli con un resistore equivalente da 2Ω.
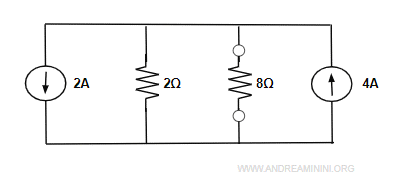
Nota. I resistori in parallelo da 6Ω e 3Ω possono essere sostituiti con un resistore equivalente $$ \frac{R_1R_2}{R_1+R_2} = \frac{6 \cdot 3}{6+3} = \frac{18}{9} $$
Ora applicando la legge di Kirchoff posso sostituire i due generatori di corrente con un generatore di corrente equivalente da 2A.
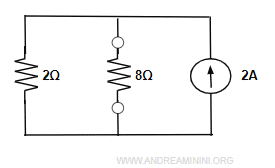
Nota. I due generatori 2A e 4A entrano nei nodi con direzioni diverse. Pertanto 4-2=2A.
Sposto i due resistori e ottengo un circuito equivalente.
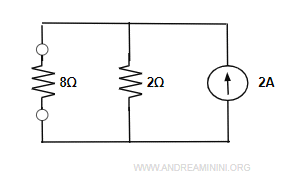
In questa forma equivalente è molto più semplice calcolare la tensione e la corrente sui terminali indicati.
Per calcolare la corrente applico il principio della divisione della corrente.
$$ i_o = \frac{R_2}{R_1+R_2} \cdot i = \frac{2}{8+2} \cdot 2 = \frac{2}{10} \cdot 2 = 0.4 A $$
Una volta ottenuta la corrente io=0.4A ai capi dei terminali, applico la legge di Ohm per calcolare la tensione ai capi dei terminali.
$$ v_0 = i \cdot R = 0.4 \cdot 8 = 3.2V $$
Ho così calcolato la tensione e la corrente ai capi dei terminali indicati nel problema.
Le condizioni della trasformazione
La trasformazione della sorgente può avvenire se sono soddisfatte alcune condizioni
- Una sorgente di tensione può essere trasformata con una corrente finita soltanto se R≠0. Se R=0 la tensione è ideale.
- Una sorgente di corrente può essere trasformata con una corrente finita soltanto se R≠∞. Se R=∞ la corrente è ideale.
E così via.
