Amplificatore operazionale invertente
Un amplificatore operazionale invertente restituisce in uscita una tensione Vout di segno opposto rispetto alla tensione in entrata Vi, amplificata o ridotta di un coefficiente k=-R2/R1. $$ V_{out} = k \cdot V_i = - \frac{R_2}{R_1} \cdot V_i $$
Ecco un esempio pratico di amp.op. invertente.
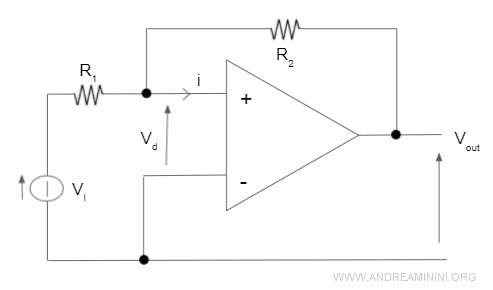
- Se il coefficiente |k|>1 l'amp.op. inverte e amplifica la tensione in ingresso.
- Se il coefficiente |k|=1 l'amp.op. inverte la tensione in ingresso.
- Se il coefficiente 0<|k|<1 l'amp.op. inverte e riduce la tensione in ingresso.
Nota. Nel disegno del circuito non ho indicato l'alimentazione Vcc e -Vcc dell'amplificatore operazionale per semplificare la rappresentazione. In ogni caso c'è. E' importante non dimenticarlo.
Come funziona l'amp.op. invertente
Per spiegare il funzionamento dell'amplificatore operazionale invertente faccio un esempio pratico.
Questo amplificatore operazionale ha una tensione in ingresso Vi=+5 e due resistori di uguale resistenza R1 = R2 = 1K Ω.
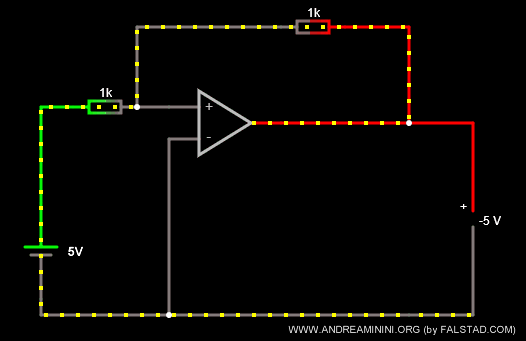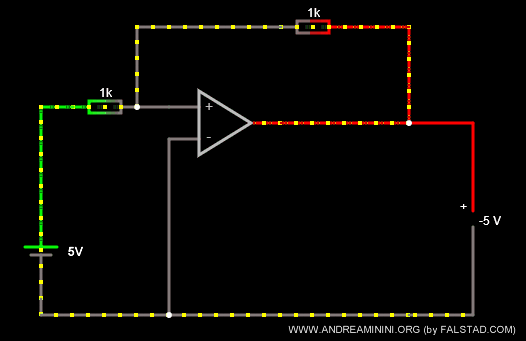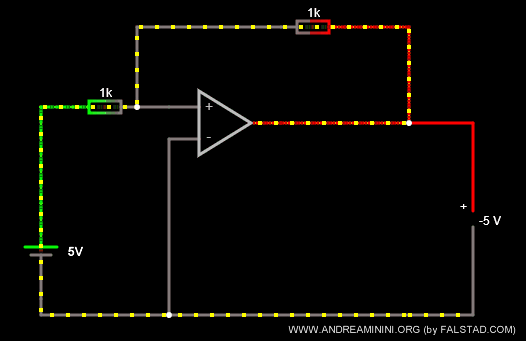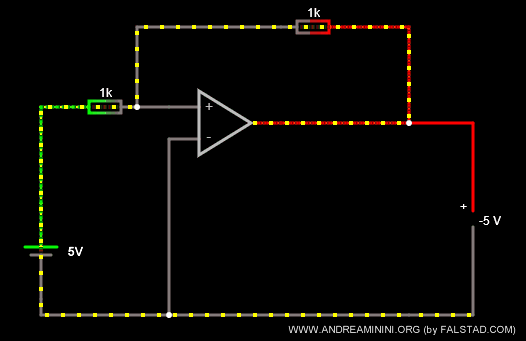
Poiché il rapporto k=-R2/R1 è uguale a k=-1, restituisce in uscita una tensione uguale ma di segno opposto Vout=-5.
E per amplificare la tensione?
Per amplificare la tensione modifico le resistenze dei resistori con R1=1k Ω e R2=2k Ω.
Ora il rapporto k=-R2/R1 è uguale a k=-2, ottengo così un effetto di amplificazione della tensione.
La tensione in uscita è Vout = -10V.
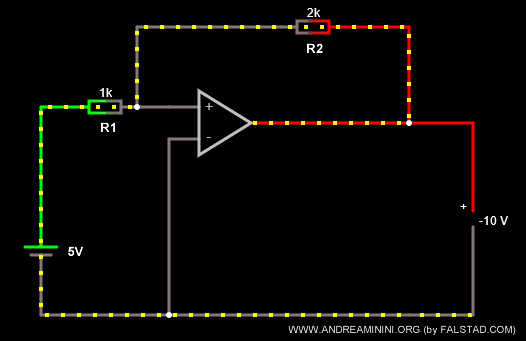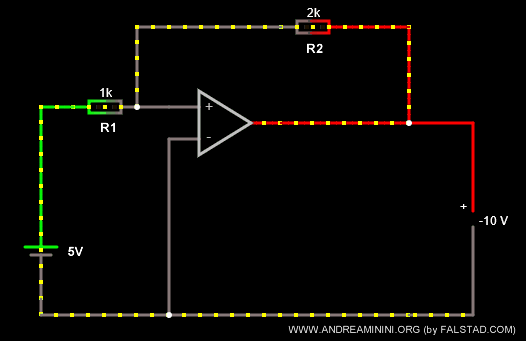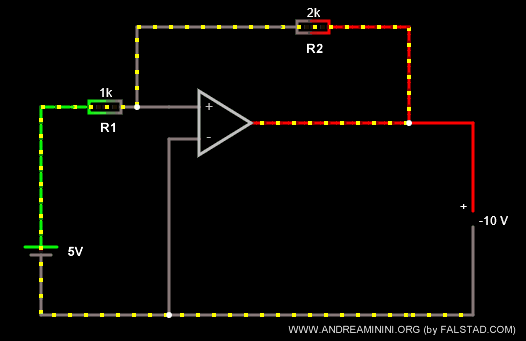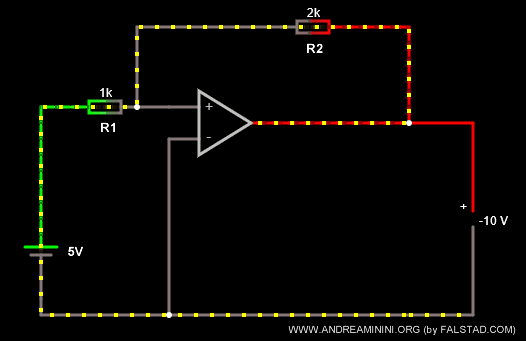
Nota. La tensione in uscita Vout è sempre invertita rispetto a quella in entrata. Ora però è anche amplificata del doppio.
E per ridurre la tensione in uscita?
Basta modificare opportunamente il rapporto tra le resistenze.
Ad esempio, modifico le resistenze dei resistori con R1=2k Ω e R2=1k Ω.
Ora il coefficiente k=-R2/R1 è uguale a k=-1/2.
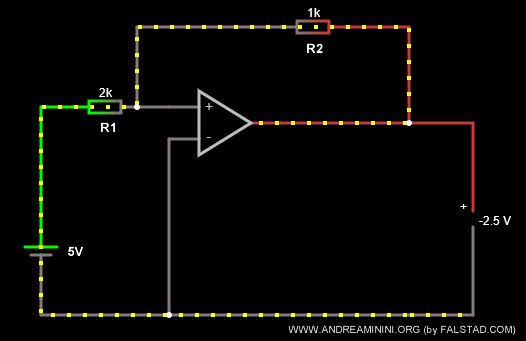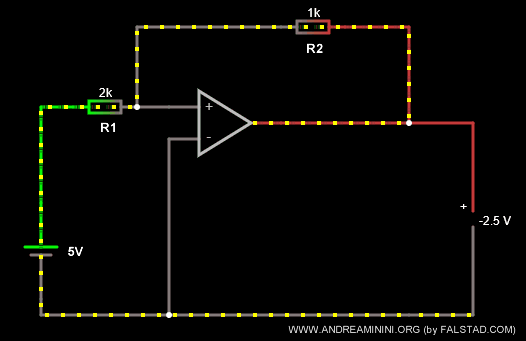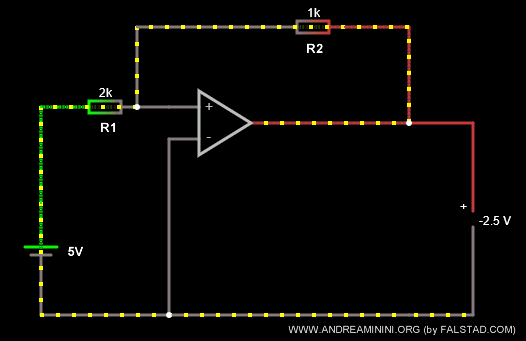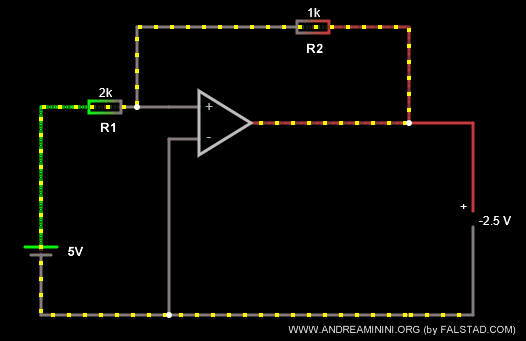
In questo modo ottengo un effetto di modulazione e riduzione della tensione a Vout = -2.5 V.
E' pari alla metà della tensione in ingresso Vi=5 V con segno opposto.
La dimostrazione
Per semplicità utilizzo un amplificatore operazionale ideale.
In un amp.op. ideale la tensione Vd=0 e la corrente i=0 sono considerate nulle per approssimazione.
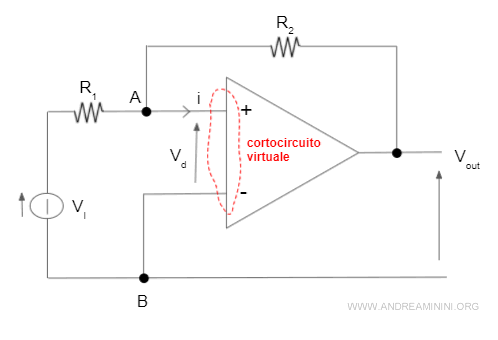
Pertanto, essendo Vd=0, tra i nodi A e B c'è un cortocircuito virtuale.
Considero la maglia m1.
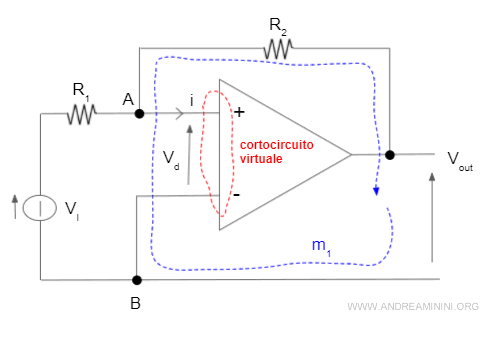
Applico il secondo principio di Kirchhoff alla maglia m1 in base al quale la somma delle tensioni in un circuito chiuso è nulla.
$$ V_d - R_2 \cdot I - V_{out} = 0 $$
Sapendo che la differenza di tensione è nulla ossia Vd=0
$$ - R_2 \cdot I - V_{out} = 0 $$
Metto in evidenza la tensione in uscita Vout
$$ V_{out} = - R_2 \cdot I $$
Ora considero la maglia m2.
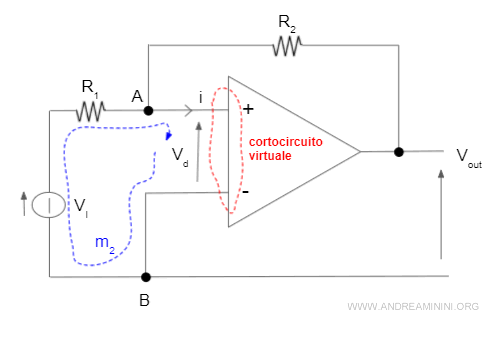
Applico il secondo principio di Kirchhoff alla maglia m2.
$$ V_i - R_1 \cdot I - V_d = 0 $$
Sapendo che Vd=0
$$ V_i - R_1 \cdot I = 0 $$
Metto in evidenza la corrente I
$$ I = \frac{V_i}{R_1} $$
Poi sostituisco la corrente nella formula della tensione in uscita e ottengo
$$ V_{out} = - R_2 \cdot I $$
$$ V_{out} = - R_2 \cdot \frac{V_i}{R_1} $$
$$ V_{out} = - \frac{R_2}{R_1} \cdot V_i $$
Ho così ottenuto la formula della tensione in uscita Vout e dimostrato il funzionamento di un amplificatore operazionale invertente.
E così via.
