Amplificatore operazionale
L'amplificatore operazionale è un circuito elettronico che si comporta come un generatore di tensione controllato in tensione.
Si tratta di un elemento circuitale attivo.
Perché si chiama amplificatore operazionale?
- E' un "amplificatore" perché l'amplificatore operazionale amplifica o riduce un segnale in ingresso. Generalmente la tensione.
- E' detto "operazionale" perché è in grado di compiere molte operazioni matematiche (addizione, sottrazione, moltiplicazione, integrazione e derivazione).
Nota. Esistono anche amplificatori operazionali che amplificano corrente, controllati in tensione o corrente.
Come funziona
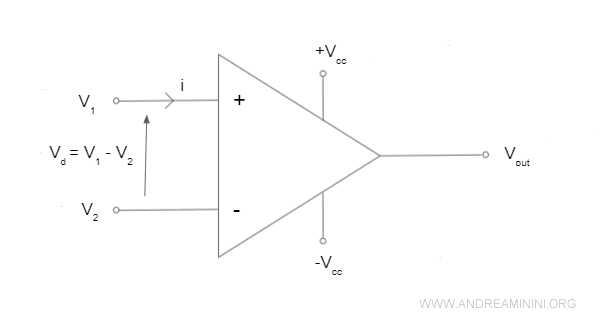
L'amplificatore operazionale è rappresentato dal simbolo di un triangolo con due ingressi V1 e V2 e una uscita Vo.

L'ingresso con il simbolo - è detto invertente perché cambia polarità all'uscita.
L'ingresso con il simbolo + è detto non invertente perché non cambia la sua polarità in uscita.
Per funzionare l'operazionale deve essere alimentato da un generatore di tensione +Vcc e -Vcc.
Nota. Spesso i terminali dell'alimentazione dell'operazionale sono omessi per semplificare la rappresentazione... ma devono esserci.
All'interno l'amplificatore operazionale è composto da due resistenze, in ingresso e in uscita, e un generatore di tensione controllato in tensione.
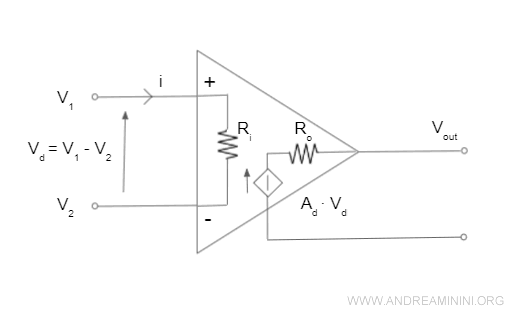
Nota. All'interno l'amplificatore operazionale è composto da due circuiti Thevenin equivalenti non collegati tra loro.
La tensione differenziale in ingresso vd=v1-v2 è la grandezza pilota del generatore di tensione controllato, moltiplicata per un coefficiente di amplificazione Ad.
$$ v_d = v_1 - v_2 $$
Se il coefficiente di amplificazione Ad è maggiore di uno, l'operazionale amplifica il segnale in ingresso.
Viceversa, se Ad è positivo ma minore di uno, l'operazionale attenua il segnale in ingresso.
Pertanto, il segnale in uscita dell'operazionale è
$$ v_o = A \cdot v_d = A \cdot (v_1 - v_2) $$
La tensione in uscita è comunque limitata dall'alimentazione dell'amplificatore operazionale tra -Vcc e +Vcc. Dove cc vuol dire corrente continua.
E' uno dei limiti degli operazionali.
$$ -v_{cc} \le v_0 \le +v_{cc} $$
Gli estremi rappresentano gli stati di saturazione positiva o negativa dell'amplificatore operazionale.
L'amplificatore operazionale ideale
L'amplificatore operazionale ideale è caratterizzato da un guadagno infinito (Ad=∞), una resistenza in ingresso infinita (Ri=∞) e una resistenza in uscita nulla (Ro=0).
A cosa serve l'amplificatore ideale?
L'operazionale ideale approssima il funzionamento dell'amplificatore operazionale, rendendone più facile l'analisi.
I parametri dell’amplificatore operazionale (Vd=0, Ri=∞, Ro=0) sono approssimazioni che semplificano i calcoli.
Esempio. La tensione differenziale Vd è in realtà molto bassa ma non nulla. Tuttavia, se la considero nulla Vd=0 i calcoli per analizzare l'amplificatore operazionale diventano più semplici.
Pur fornendo un'analisi approssimata, è abbastanza accettabile perché gli amplificatori operazionali reali sono spesso caratterizzati da guadagni elevati e resistenze in ingresso elevate.
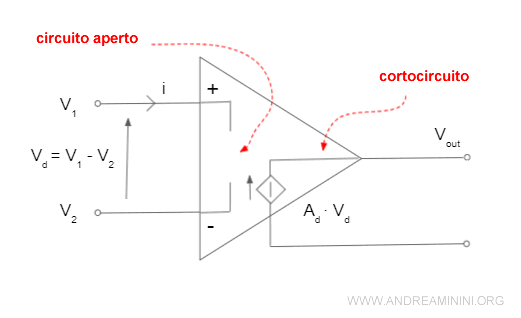
Lo schema di un amplificatore operazionale si ottiene sostituendo alla resistenza in ingresso un bipolo circuito aperto e alla resistenza in uscita un bipolo cortocircuito.
Nota. Una resistenza tendente a infinito equivale a un circuito aperto. Viceversa, una resistenza tendente a zero equivale a un cortocircuito.
Essendo un circuito aperto in ingresso, in un operazionale ideale le correnti in ingresso sono nulle per il primo principio di Kirchhoff.
La corrente in uscita non è detto però che sia nulla.
La tensione tra i terminali in ingresso è molto bassa, tendente a zero. Quindi è trascurabile.
$$ v_d = v_2 - v_1 \approx 0 $$
Pertanto le due tensioni sono uguali v2=v1.
E' un'ulteriore semplificazione dell'analisi.
$$ i_1 = i_2 = 0 $$
Le caratteristiche dell'amplificatore operazionale ideale danno vita a un nuovo bipolo matematico (non reale) detto cortocircuito virtuale.
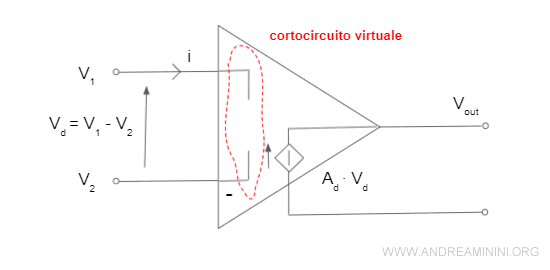
E’ detto cortocircuito virtuale perché non è un vero cortocircuito.
Nel cortocircuito virtuale dell'amplificatore operazionale ideale si verifica questa situazione
- La corrente non scorre (i=0)
Per il primo principio di Kirchhoff a corrente non scorre in un circuito aperto. - La tensione è nulla (v=0)
La differenza di tensione Vd è tendente a zero come in un cortocircuito reale.
Nota. Queste caratteristiche sono uniche perché in un cortocircuito reale la tensione è nulla ma la corrente può essere qualsiasi. Viceversa, in un circuito aperto reale la corrente è nulla ma la tensione può essere qualsiasi.
E così via.
