Amplificatori operazionali non invertenti
Un amplificatore operazionale non invertente genera una tensione in uscita Vout con lo stesso segno della tensione in entrata Vi, amplificata per un coefficiente k. $$ V_{out} = \frac{R_1+R_2}{R_1} \cdot V_i $$
Ecco un esempio di circuito amplificatore operazionale non invertente.
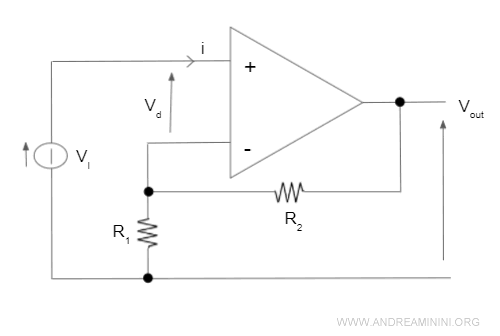
Il coefficiente k dell'amplificatore operazionale non invertente può essere maggiore o uguale a 1.
- Se k=1 l'amp.op. restituisce in uscita la stessa tensione in ingresso (Vout=Vi).
- Se k>1 l'amo.op. restituisce in uscita una tensione maggiore rispetto a quella in ingresso (Vout>Vi).
Nota. A differenza degli amplificatori operazionali invertenti, un amplificatore non invertente non riesce a ridurre un segnale perché k non può essere minore di 1 (ossia k≥1). Al massimo se la resistenza R2=0 è nulla, il coefficiente k è unitario ossia k=R1/R1=1.
Funzionamento e spiegazione
Faccio un esempio pratico per spiegare come funziona l'amplificatore operazionale non invertente.
In questo circuito il generatore di tensione fornisce all'amp.op. una tensione in ingresso di +5V.
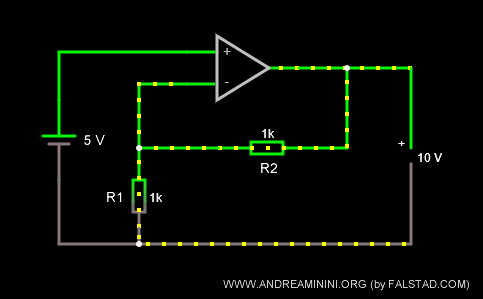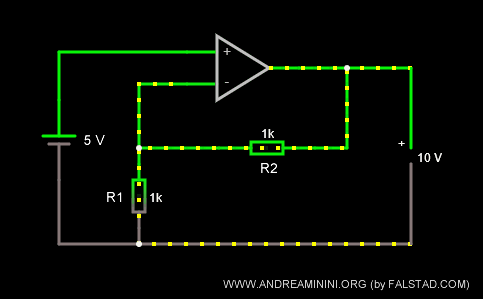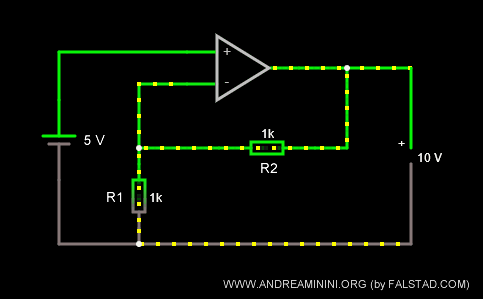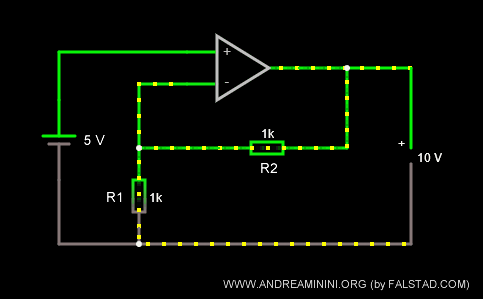
I resistori hanno la stessa resistenza R1=R2=1k Ω.
Quindi, il coefficiente di amplificazione k è pari a due.
$$ k = \frac{R_1 + R_2}{R_1} = \frac{1000 \ Ω + 1000 \ Ω}{1000 \ Ω} = 2 $$
Pertanto, l'amp.op. genera una tensione in uscita pari al doppio Vout=10V rispetto alla tensione in ingresso Vi=5.
$$ V_{out} = k \cdot V_i = 2 \cdot 5 \ V = 10 V $$
ll segno della tensione in entrata e in uscita è lo stesso.
Nota. Ogni amplificatore operazionale è alimentato da un generatore ±Vcc che non viene indicato nel circuito per semplicità. E' opportuno non dimenticarlo.
Esempio 2
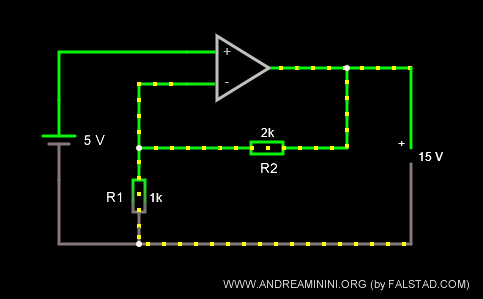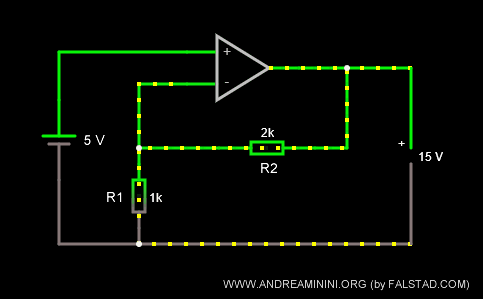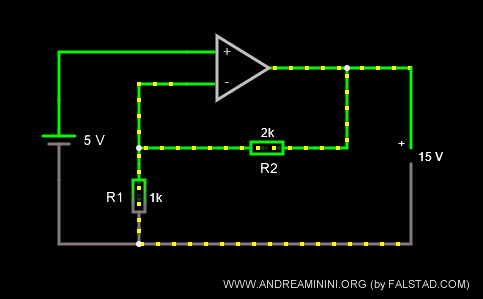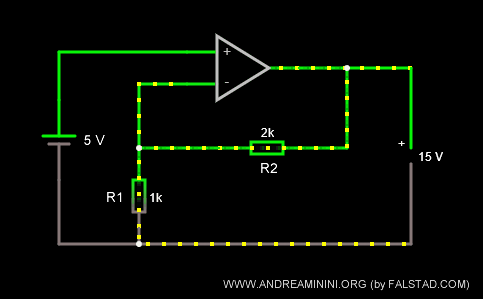
Se raddoppio la resistenza R2=2k Ω lasciando R1=1k Ω, il coefficiente di amplificazione k diventa pari a 3.
$$ k = \frac{R_1 + R_2}{R_1} = \frac{1000 \ Ω + 2000 \ Ω}{1000 \ Ω} = 3 $$
In questo caso, la tensione in uscita diventa diventa Vout=15V.
$$ V_{out} = k \cdot V_i = 3 \cdot 5 \ V = 15 V $$
Il triplo della tensione in entrata Vi=5.
Anche in questo caso il segno della tensione in uscita è uguale a quello della tensione in entrata.
La dimostrazione
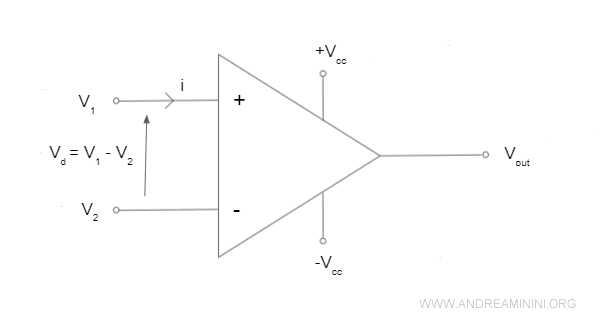
Per dimostrare il funzionamento dell'amplificatore operazionale non invertente, utilizzo un amplificatore operazionale ideale.
Essendo un amp.op. ideale, la corrente non scorre nell'amplificatore (i=0).
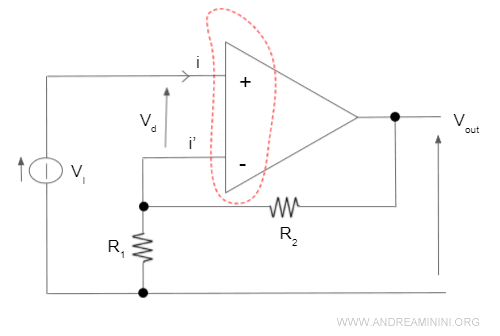
Per il primo principio di Kirchhoff anche la corrente i'=0 è nulla.
$$ +i - i' = 0 $$
$$ +i = i' $$
Poiché i=0 anche i' è nullo.
Applico il secondo principio di Kirchhoff alla maglia m2.
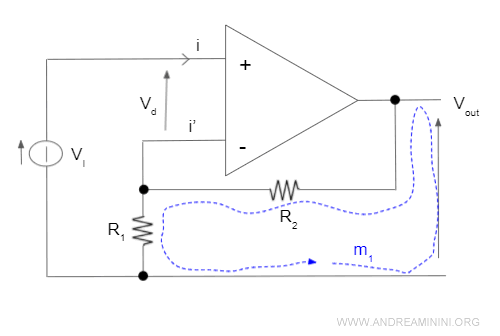
Secondo il 2° principio di Kirchhoff la somma delle tensioni in un circuito chiuso è nulla.
$$ V_{out} - R_2 \cdot I - R_1 \cdot I = 0 $$
$$ V_{out} = R_2 \cdot I + R_1 \cdot I $$
$$ V_{out} = (R_1 + R_2) \cdot I $$
Ora applico il secondo principio di Kirchhoff alla maglia m1.
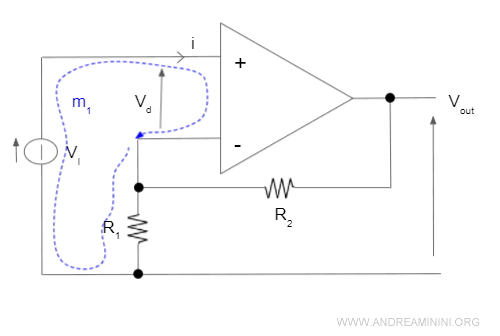
Anche in questo caso la somma delle tensioni nella maglia deve essere nulla.
$$ V_i - V_d - R_1 \cdot I = 0 $$
In un amplificatore operazionale ideale la differenza di tensione Vd=0 è nulla.
$$ V_i - R_1 \cdot I = 0 $$
Quindi, la corrente nel circuito è pari a
$$ I = \frac{V_i}{R_1} $$
Sostituisco la formula della corrente che ho appena ricavato nella formula della tensione in uscita.
$$ V_{out} = (R_1 + R_2) \cdot I $$
$$ V_{out} = (R_1 + R_2) \cdot \frac{V_i}{R_1} $$
E ottengo la la formula della tensione in uscita dell'amplificatore operazionale non invertente.
$$ V_{out} = \frac{R_1 + R_2}{R_1} \cdot V_i $$
In questo modo ho dimostrato il funzionamento dell'amp.op. non invertente.
E così via.
