Automi semi-markoviani
I Semi Markov Process (SMP) sono una classe di processi in cui la proprietà memoryless di Markov è meno rigida.
Negli automi semi-markoviani la condizione "no state age memory" non è rispettata.
L'automa conosce il numero di volte/tempo in cui è passato per uno stato.
Pertanto, non è più necessario distribuire esponenzialmente il tempo di intervento.
La probabilità di transizione dallo stato xi allo stato xj dipende dal tempo di attivazione di ogni evento attivo A(xi) nello stato xi, ossia per quanto tempo ogni evento è rimasto attivo. $$ P \{ x_j|x_i \} = λ_{i,j} \{ φ_{e_1},φ_{e_2}, ... ,φ_{e_n}, \} $$
Dove φe indica il tempo di attività dell'evento "e" a partire dall'inizio.
Il vettore λi,j contiene i tempi di attività di tutti gli eventi ammissibili dallo stato xi allo stato xj.
L'automa non conosce la storia degli eventi passati ma sa quanto tempo ha già trascorso in un evento.
Quest'ultima informazione influisce sulla probabilità di transizione da un evento a un altro.
Un esempio pratico
Per semplicità l'automa si trova nello stato xi=x(τ).
La transizione allo stato xj=x(τ+dτ) ha la seguente probabilità.
$$ P(x(τ+dτ)|x(τ)=x_i) = λ \{ φ_{e_1} ,φ_{e_2}, ... ,φ_{e_n} \} $$
Prendo in considerazione un evento specifico, ad esempio e1.
L'orologio dell'evento ha un valore casuale θe1 in base alla distribuzione ψ(θ).
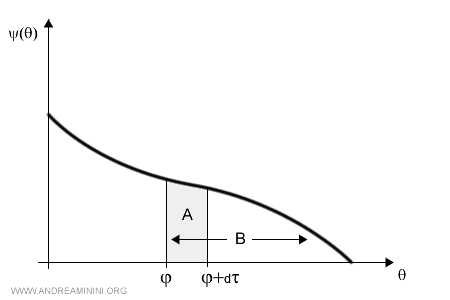
L'area A indica il ritardo di attivazione dell'evento tra φ e φ+dτ.
L'area B indica il ritardo di attivazione dell'evento con θe1>φ.
Nota. L'area B misura la probabilità in cui il ritardo di attivazione θe1 è maggiore del tempo di attivazione φ dell'evento ( tempo in cui l'evento è rimasto attivo ). L'area A, invece, il caso in cui il ritardo di attivazione θe1 sia minore del tempo di attivazione. Ovviamente, l'area A è un sottoinsieme dell'area B.
La probabilità condizionata della transizione è
$$ P(A|B) = \frac{A}{B} $$
Pertanto, la transizione dallo stato x(τ) allo stato x(τ+dτ) è determinata dal ritardo di attivazione θe1 e dal tempo di attivazione φ, ossia da quanto tempo l'evento è già stato attivo a partire dall'inizio ( state age memory ).
L'automa non conosce la storia passata degli eventi come i processi markoviani. Tuttavia, conosce il tempo di attivazione.
Per questa ragione è un processo semi-markoviano.
E così via.
Nota. Nel caso particolare in cui la distribuzione ψ(θ) dei ritardi di attivazione è esponenziale, il processo diventa markoviano. Quindi, la classe degli automi semi-markoviani contiene al suo interno anche una sottoclasse di processi markoviani. Per questa ragione, spesso i processi semi-markoviani sono anche detti Generalized Semi-Markov Process (GSMP) ossia processi semi-markoviani generalizzati.
