Sensibilità ai disturbi
La sensibilità (o sensitività) ai disturbi misura l'effetto di un segnale di disturbo d(t) su un sistema.
L'analisi della sensitività ai disturbi cambia a seconda se il sistema è a catena diretta o a retroazione.
Disturbi in un sistema a catena diretta
In un sistema a catena di amplificazione diretta (senza retroazione) l'uscita viene modificata dal disturbo in modo proporzionale.
Prendo in considerazione un sistema a catena diretta con due blocchi G1 e G2.
Il segnale di disturbo D(s) influisce sull'uscita del primo blocco, quindi sull'entrata del secondo blocco.
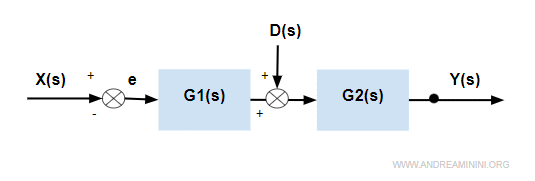
La funzione di trasferimento del sistema senza il disturbo è la seguente:
$$ \frac{Y(s)}{X(s)} = G_1(s) G_2(s) $$
quindi l'uscita del sistema è
$$ Y(s) = G_1(s) G_2(s) X(s) $$
Ora devo aggiungere l'effetto del disturbo sull'uscita Yd(s)
$$ Y(s) = G_1(s) G_2(s) X(s) + Y_d(s) $$
Il disturbo agisce soltanto sul secondo blocco
$$ Y(s) = G_1(s) G_2(s) X(s) + G_2(s) D(s) $$
Analizzo soltanto l'effetto del segnale di disturbo D(s)
$$ Y_d (s) = G_2(s) \cdot D(s) $$
Il rapporto segnale/disturbo mette in rapporto l'uscita del sistema senza disturbo Y(s) con l'impatto del disturbo sull'uscita Yd(s)
$$ \frac{Y(s)}{Y_d(s)} = \frac{G_1(s) G_2(s) X(s) }{G_2(s) D(s)} $$
Assegno il simbolo G(s) alla funzione di trasferimento del sistema G1(s)G2(s)
$$ \frac{Y(s)}{Y_d(s)} = \frac{G(s) X(s) }{G_2(s) D(s)} $$
$$ \frac{Y(s)}{Y_d(s)} = \frac{G(s)}{G_2(s)} \cdot \frac{X(s) }{D(s)} $$
Disturbi in un sistema a retroazione
L'effetto di un disturbo sull'uscita in un sistema a retroazione il disturbo è il seguente $$ Y_d(s) = \frac{G(s)}{1+G(s)H(s)} $$
Prendo in considerazione come esempio uno schema con due blocchi e una retroazione.
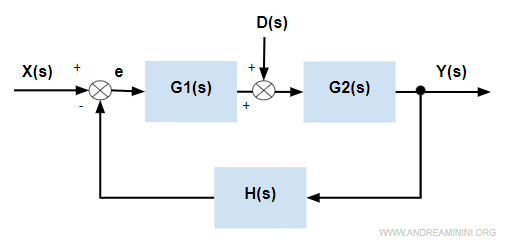
Nota. In questo caso ho preso in considerazione due blocchi attuatori G1(s) e G2(s). Potrebbe anche trattarsi di controllore G1(s)=C(s) e un processo atturatore G2(s). Potrebbe anche trattarsi di due attuatori.
La funzione di trasferimento del sistema senza il disturbo è la seguente
$$ \frac{Y(s)}{X(s)} = \frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)} $$
$$ Y(s) = \frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)} X(s) $$
Nella funzione di trasferimento aggiungo anche l'effetto del disturbo sull'uscita del sistema Yd(s)
$$ Y(s) = \frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)} X(s) + Y_d(s) $$
Il disturbo D(s) influisce sul segnale in entrata al secondo blocco G2(s) e in retroazione sul resto del sistema
$$ Y(s) = \frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)} X(s) + \frac{G_2(s)}{1+G_1(s)G_2(s)H(s)} D(s) $$
Analizzo l'effetto del disturbo sul sistema
$$ Y_d(s) = \frac{G_2(s)}{1+G_1(s)G_2(s)H(s)} D(s) $$
che posso riscrivere in forma equivalente per mettere in evidenza la funzione di sensitività
$$ Y_d(s) = \frac{1}{1+G_1(s)G_2(s)H(s)} G_2(s)D(s) $$
Ponendo s=jω per passare alle pulsazioni
$$ Y_d(jω) = \frac{1}{1+G_1(jω)G_2(jω)H(jω)} \cdot G_2(jω)D(s) $$
il rapporto ((1+G_1(jω)G_2(jω)H(jω))-1 è detto funzione di sensibilità ( o funzione di sensitività ).
$$ S(jω) = \frac{1}{1+G_1(jω)G_2(jω)H(jω)} $$
Cos'è la funzione di sensitività? E' il fattore moltiplicativo del disturbo della funzione di trasferimento dovuto alla retroazione che produce errori parametrici nel sistema. Cambia a seconda della pulsazione ω.
Quindi l'uscita del sistema dopo un disturbo è il prodotto tra la funzione di sensitività e il blocco di amplificazione soggetto al disturbo
$$ Y_d(jω) = S(jω) \cdot G_2(jω) D(s) $$
e la funzione di trasferimento del disturbo
$$ \frac{Y_d(jω)}{D(s)} = S(jω) \cdot G_2(jω) $$
Nota. Se la funzione di risonanza vale uno, non ci sono errori. Se la funzione di risonanza è molto più grande di 1 si presenta una risonanza, se è molto più piccola di 1 si presenta una riduzione del segnale.
Il rapporto segnale/disturbo mette in rapporto l'uscita del sistema senza disturbo Y(s) con l'impatto del disturbo sull'uscita Yd(s)
$$ \frac{Y(s)}{Y_d(s)} = \frac{ \frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)} X(s) }{ \frac{1}{1+G_1(s)G_2(s)H(s)} G_2(s)D(s) } $$
Per semplificare assegno il simbolo G(s)=G1(s)+G2(s) alla funzione di trasferimento
$$ \frac{Y(s)}{Y_d(s)} = \frac{ \frac{G(s)}{1+G(s)H(s)} X(s) }{ \frac{1}{1+G(s)H(s)} G_2(s)D(s) } $$
$$ \frac{Y(s)}{Y_d(s)} = \frac{G(s)X(s)}{1+G(s)H(s)} \frac{ 1+G(s)H(s) }{ G_2(s)D(s)} $$
$$ \frac{Y(s)}{Y_d(s)} = \frac{G(s)X(s)}{ G_2(s)D(s) } $$
E' ora interessante vedere come cambia il confronto senza considerare la retroazione nel sistema Y'(s).
$$ \frac{Y'(s)}{Y_d(s)} = \frac{ G(s) X(s) }{ \frac{1}{1+G(s)H(s)} G_2(s)D(s) } $$
$$ \frac{Y'(s)}{Y_d(s)} = G(s) X(s) \cdot \frac{1+G(s)H(s) }{ G_2(s)D(s) } $$
$$ \frac{Y'(s)}{Y_d(s)} = 1+G(s)H(s) \cdot \frac{ G(s) }{ G_2(s) } \frac{ X(s) }{ D(s) } $$
Il rapporto Y'(s)/Yd(s) è più grande del precedente Y(s)/Yd(s)
$$ \frac{Y'(s)}{Y_d(s)} \ge \frac{Y(s)}{Y_d(s)} $$
perché agisce il fattore moltiplicativo del disturbo 1+G(s)H(s) tanto più è grande il guadagno dell'anello.
$$ 1+G(s)H(s) \cdot \frac{ G(s) }{ G_2(s) } \frac{ X(s) }{ D(s) } \ge \frac{ G(s) }{ G_2(s) } \frac{ X(s) }{ D(s) } $$
E così via
