Criterio di Routh
Il criterio di Routh permette di calcolare i poli sul piano reale di una funzione di trasferimento razionale fratta.
A cosa serve?
E' utile per capire se un sistema lineare stazionario è stabile oppure no.
Generalmente, il calcolo delle radici/poli è un'operazione complessa. Il criterio di Routh lo semplifica.
Inoltre, il criterio di Routh è una condizione necessaria e sufficiente della stabilità.
Promemoria. Un sistema lineare stazionario, ossia con funzione di trasferimento razionale fratta, è stabile se tutti i poli della parte reale sono negativi.
Dimostrazione e spiegazione
Prendo in considerazione l'equazione caratteristica di un sistema
$$ a_n s^n + a_{n-1}s^{n-1}... + a_1 s^1 + a_0 = 0 $$
Per semplicità considero i coefficienti an e a0 positivi.
Il sistema è asintoticamente stabile se tutte le radici di parte reale sono negative.
Una condizione necessaria ma non sufficiente della stabilità asintotica è che tutti i coefficienti a0,...,an siano positivi.
$$ a_0>0 \\ a_1 >0 \\ \vdots \\ a_n>0 $$
Nota. La condizione necessaria di stabilità vale anche se tutti i coefficienti sono negativi. In generale, il sistema è stabile se i coefficienti hanno tutti lo stesso segno.
Le radici dell'equazione possono essere radici reali o radici complesse.
Ad esempio, in un'equazione ci possono essere k radici reali (p1,p2,...pk) e m radici complesse (σ1+jω1,σ2+jω2,...,σm+jωm).
Posso riscrivere il polinomio al primo membro dell'equazione nella forma fattorizzata.
$$ a_n(s-p_1) ... (s-p_k) (s-σ_1-jω_1)(s-σ_1+jω_1) ... (s-σ_m-jω_m)(s-σ_m+jω_m) $$
Se le radici di parte reale hanno segno negativo, i coefficienti a dell'equazione sono tutti positivi.
E' la condizione necessaria della stabilità del sistema.
Per avere la certezza che il sistema è stabile devo calcolare la tabella di Routh.
Nota. Prima di costruire la tabella di Routh è sempre oppurtuno verificare se la condizione necessaria è soddisfatta. Se quest'ultima non è soddisfatta, il sistema è sicuramente instabile.
Come costruire la tabella di Routh
Dispongo i coefficienti dell'equazione caratteristica in un tabella detta tabella di Routh, alternandoli sulle prime due righe.
$$ \begin{array}{c|lcr} n & a_n & a_{n-2} & a_{n-4} & ... \\ n-1 & a_{n-1} & a_{n-3} & a_{n-5} & ... \\ \hline n-2 & ... & ... & ... & \\ n-3 & ... & ... & ... & \\ ... & ... & ... & ... & \\ 2 & ... & ... & ... & \\ 1 & ... & ... & ... & \\ 0 & ... & ... & ... & \end{array} $$
Nota. Il primo elemento an va messo sulla prima riga, il secondo elemento an-1 nella seconda riga sotto il primo elemento. Il terzo elemento an-2 sulla prima riga, il quarto elemento an-3 nella seconda riga sotto il terzo elemento. E via dicendo.
La tabella è composta da n+1 righe fino alla riga zero.
$$ \begin{array}{c|lcr} n & a_n & a_{n-2} & a_{n-4} & a_{n-6} & ... \\ n-1 & a_{n-1} & a_{n-3} & a_{n-5} & a_{n-7} & ... \\ \hline n-2 & x_{n-2} & x_{n-4} & x_{n-6} & x_{n-8} \\ n-3 & x_{n-3} & x_{n-5} & x_{n-7} & x_{n-9} \\ ... & ... & ... & ... & \\ 2 & x_{2} & x_{0} & ... & \\ 1 & x_{1} & ... & ... & \\ 0 & x_{0} & ... & ... & \end{array} $$
Per completare la tabella aggiungo in pedice anche il numero della colonna (h=1,... )
$$ \begin{array}{c|lcr} n & a_n & a_{n-2} & a_{n-4} & a_{n-6} & ... \\ n-1 & a_{n-1} & a_{n-3} & a_{n-5} & a_{n-7} & ... \\ \hline n-2 & x_{n-2,1} & x_{n-4,2} & x_{n-6,3} & x_{n-8,4} \\ n-3 & x_{n-3,1} & x_{n-5,2} & x_{n-7,3} & x_{n-9,4} \\ ... & ... & ... & ... & \\ 2 & x_{2,1} & x_{0,2} & ... & \\ 1 & x_{1,1} & ... & ... & \\ 0 & x_{0,1} & ... & ... & \end{array} $$
Per calcolare il valore di ogni elemento delle successive righe della tabella, utilizzo la seguente formula:
$$ x_{i,h} = - \frac{1}{x_{i+1,1}} \cdot \: det \begin{vmatrix} x_{i+2,1} & x_{i+2,h+1} \\ x_{i+1,1} & x_{i+1,h+1} \end{vmatrix} $$
Dove i è il numero di riga ( es. n-2 , n-3, ecc.) mentre h è il numero di colonna da 1 in poi.
Nota. Ecco un esempio pratico di funzionamento dell'algoritmo di Routh per la costruzione della tabella.
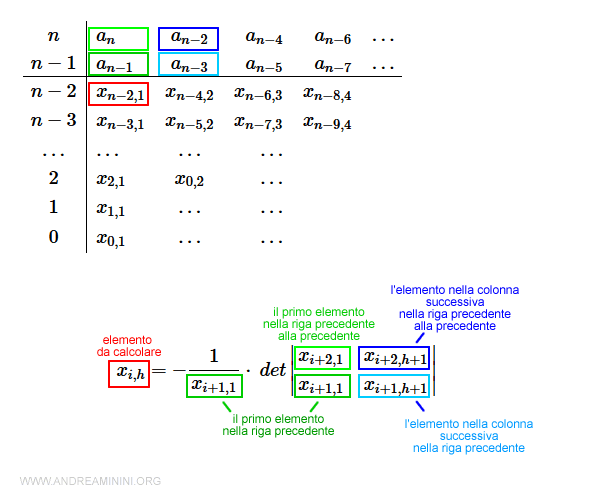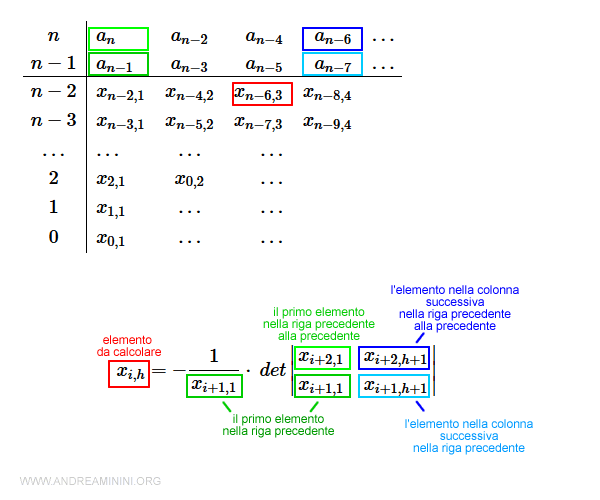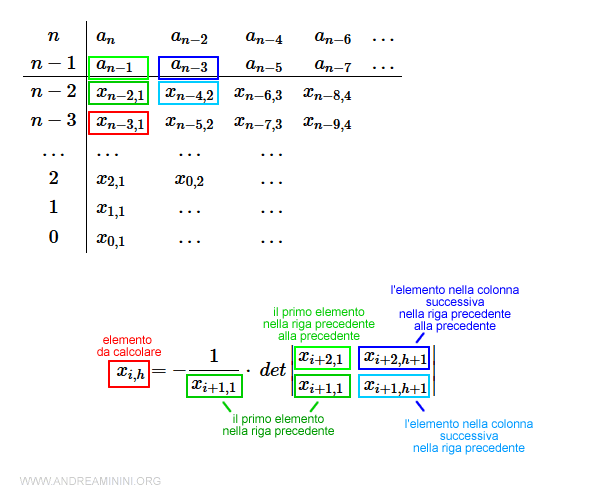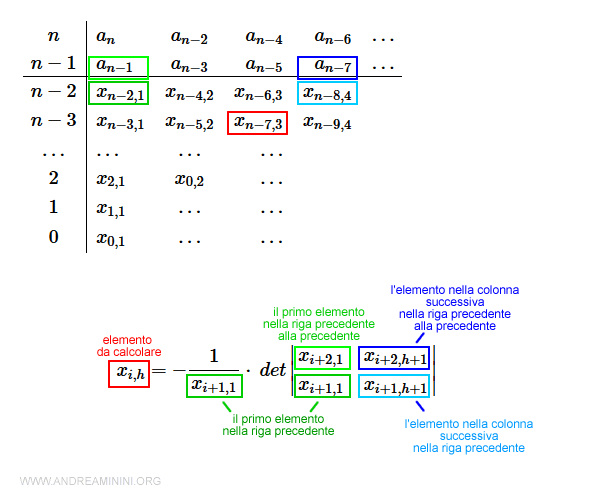
Il denominatore xi+1,1 è il primo elemento della riga precedente all'elemento da calcolare xi,h ed è costante per tutti gli elementi di una riga. La prima colonna del determinante è composta dai primi elementi delle due righe precedenti all'elemento da calcolare xi,h. Anche in questo caso sono valori costanti per tutti gli elementi di una riga. La seconda colonna del determinante è composta dagli elementi della colonna successiva (h+1) nelle due righe precedenti all'elemento da calcolare xi,h. Questi ultimi due valori variano a seconda dell'elemento che si sta calcolando.
Quando in una riga trovo un elemento nullo, considero nulli tutti i successivi e passo alla riga seguente.
Il risultato finale è una tabella triangolare.
Le righe della tabella hanno una lunghezza decrescente e l'ultima riga ha un solo elemento.
- Ecco alcuni consigli pratici per semplificare il calcolo
- Consiglio 1 Durante il calcolo potrebbero presentarsi dei numeri frazionari. Ad esempio, una riga ha gli elementi 17/3 23/3 e 7/3. Per semplificare i calcoli della riga successiva posso moltiplicare tutti gli elementi della riga per un intero positivo. Moltiplicando tutti gli elementi della riga per 3 ottengo la riga 17 23 e 7. In questo modo la riga successiva è più semplice da calcolare. Il risultato finale dell'analisi di Routh non cambia.
- Consiglio 2 Se durante il calcolo del determinante il secondo elemento della seconda colonna è nullo, il risultato è sempre il primo elemento della seconda colonna. $$ x_{i,h} = - \frac{1}{a} \cdot \: det \begin{vmatrix} b & c \\ a & 0 \end{vmatrix} = - \frac{1}{a} \cdot [ (b \cdot 0) - (c \cdot a) ] = - \frac{- (c \cdot a) }{a} = c $$
- Consiglio 3. Se durante il calcolo il primo elemento di una riga è nullo, posso subito concludere che c'è almeno una radice di parte reale positiva. Quindi, senza ultimare i calcoli posso affermare che il sistema è instabile.
Se tutti gli elementi della tabella di Routh sono diversi da zero, la tabella è detta ben definita.
Il sistema è instabile se la tabella non è ben definita.

L'analisi della prima colonna è molto importante perché identifica le condizioni necessarie e sufficienti per la stabilità del sistema.
Il teorema di Routh
Secondo il teorema di Routh il sistema è stabile se gli elementi della prima colonna hanno tutti lo stesso segno (positivo o negativo).
Pertanto, è sufficiente che ci sia un cambio di segno nella prima colonna per dimostrare l'instabilità del sistema.
La prima colonna della tabella di Routh mi consente di conoscere anche il numero delle radici di parte reale negativa.
- Il numero delle radici di parte reale negativa è pari al numero delle permanenze di segno della prima colonna.
- Ogni cambio di segno nella prima colonna indica la presenza di una radice nulla o positiva.
Un esempio pratico
Ho il polinomio di quarto grado
$$ P(s) = 8s^4+3s^3+7s^2+2s+1 $$
Verifico se la condizione necessaria di stabilità è soddisfatta, ossia se tutti i coefficienti hanno lo stesso segno.
La condizione necessaria di stabilità è soddisfatta.
Nota. Se il sistema non supera questo primo controllo è inutile continuare l'analisi.
Costruisco la tabella di Routh per verificare le condizioni necessarie e sufficienti di stabilità.
Le prime due righe ( 4 e 3 ) della tabella sono le seguenti:
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & \\ 1 \:\:\: & \\ 0 \:\:\: & \end{array} $$
A questo punto comincio a calcolare le righe restanti.
Riga 2
Calcolo il primo elemento della riga 2
$$ x_{2,1} = - \frac{1}{3} \cdot \begin{vmatrix} 8 & 7 \\ 3 & 2 \end{vmatrix} = \frac{5}{3} $$
Poi aggiorno la tabella
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & \frac{5}{3} \:\:\: & \\ 1 \:\:\: & \\ 0 \:\:\: & \end{array} $$
Calcolo il secondo elemento della riga 2
$$ x_{2,2} = - \frac{1}{3} \cdot \begin{vmatrix} 8 & 1 \\ 3 & 0 \end{vmatrix} = 1 $$
Poi aggiorno la tabella
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & \frac{5}{3} \:\:\: & 1 \:\:\: \\ 1 \:\:\: & \\ 0 \:\:\: & \end{array} $$
Calcolo il terzo elemento della riga 2
$$ x_{2,3} = - \frac{1}{3} \cdot \begin{vmatrix} 8 & 0 \\ 3 & 0 \end{vmatrix} = 0 $$
Poiché è nullo, il calcolo della riga 2 finisce qui.
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & \frac{5}{3} \:\:\: & 1 \:\:\: \\ 1 \:\:\: & \\ 0 \:\:\: & \end{array} $$
Nella riga 2 ci sono dei numeri frazionari.
Posso eliminarli moltiplicando tutti i termini della riga per 3.
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & \frac{5}{3} \cdot 3 \:\:\: & 1 \cdot 3 \:\:\: \\ 1 \:\:\: & \\ 0 \:\:\: & \end{array} $$
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & \\ 0 \:\:\: & \end{array} $$
Riga 1
Calcolo il primo elemento della riga 1
$$ x_{1,1} = - \frac{1}{5} \cdot \begin{vmatrix} 3 & 2 \\ 5 & 3 \end{vmatrix} = \frac{1}{5} $$
Poi aggiorno la tabella
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & \frac{1}{5} \:\:\: \\ 0 \:\:\: & \end{array} $$
Calcolo il secondo elemento della riga 1
$$ x_{1,2} = - \frac{1}{5} \cdot \begin{vmatrix} 3 & 0 \\ 5 & 0 \end{vmatrix} = 0 $$
Poiché è nullo, il calcolo della riga 1 finisce qui.
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & \frac{1}{5} \:\:\: \\ 0 \:\:\: & \end{array} $$
Nella riga 1 c'è un numero frazionario.
Posso eliminarlo moltiplicando tutti i termini della riga per 5.
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & \frac{1}{5} \cdot 5 \:\:\: \\ 0 \:\:\: & \end{array} $$
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & 1 \:\:\: \\ 0 \:\:\: & \end{array} $$
Riga 0
Calcolo il primo elemento della riga 0
$$ x_{0,1} = - \frac{1}{1} \cdot \begin{vmatrix} 5 & 3 \\ 1 & 0 \end{vmatrix} =3 $$
Poi aggiorno la tabella
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & 1 \:\:\: \\ 0 \:\:\: & 3 \:\:\: \end{array} $$
Calcolo il secondo elemento della riga 0
$$ x_{0,1} = - \frac{1}{1} \cdot \begin{vmatrix} 5 & 0 \\ 1 & 0 \end{vmatrix} = 0 $$
E' nullo. Quindi la riga 0 termina qui.
Non essendoci altre righe la tabella di Routh è completa.
$$ \begin{array}{c|lcr} 4 \:\:\: & 8 \:\:\: & 7 \:\:\: & 1 \:\:\: \\ 3 \:\:\: & 3 \:\:\: & 2 \:\:\: & \\ \hline 2 \:\:\: & 5 \:\:\: & 3 \:\:\: \\ 1 \:\:\: & 1 \:\:\: \\ 0 \:\:\: & 3 \:\:\: \end{array} $$
L'analisi della tabella di Routh
Tutti i coefficienti della prima colonna della tabella di Routh hanno lo stesso segno.
Non si verifica nemmeno una variazione di segno.
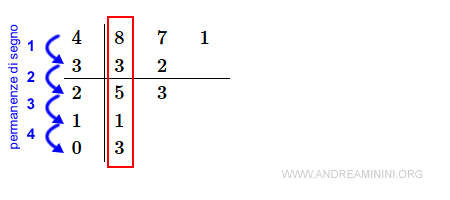
Quindi, tutte le radici sono di parte reale negativa.
Posso concludere che il sistema è stabile.
Nota. Essendoci quattro permanenze di segno, il polinomio P(s) ha quattro radici di parte reale negativa.
E così via.
