Sistema elementare del secondo ordine

Un sistema del secondo ordine ha una funzione di trasferimento nella seguente forma a meno di un fattore costante $$ G(s) = \frac{1}{1+2δ \frac{s}{ω_n}+\frac{s^2}{ω_n^2}} $$ oppure $$ G(s) = \frac{ω^2_n}{s^2+2δω_ns+ω^2_n} $$

Dove δ è il coefficiente di smorzamento e ω la pulsazione naturale.

I parametri dipendono dalla posizione dei poli nel piano complesso.

Nota. In genere una funzione del trasferimento ha una coppia di poli dominanti complessi e coniugati tra loro che si trovano vicini all'asse immaginario.

I sistemi del secondo ordine hanno una risposta simile ai sistemi con retroazione.

Hanno un tipico comportamento oscillatorio smorzato.

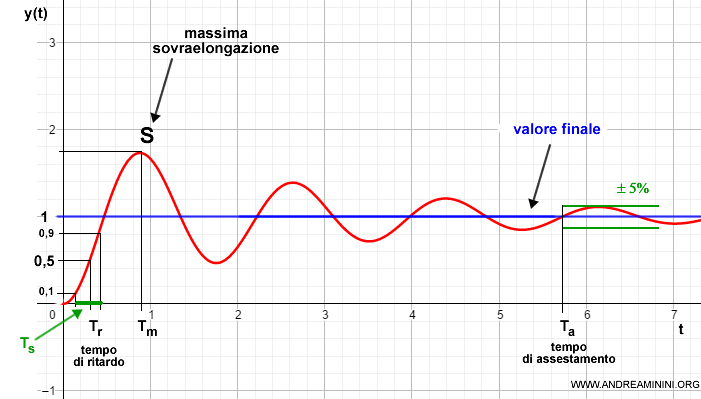
I principali parametri sono:

• La massima sovraelongazione
  E' la differenza tra il massimo valore in uscita e il valore finale. E' anche detto massimo sorpasso S.
• Il tempo di ritardo
  E' il tempo necessario T_r per ottenere il 50% del valore finale.
• Il tempo si salita
  E' il tempo necessario T_s per passare dal 10% al 90% del valore finale.
• Il tempo di assestamento
  E' il tempo necessario T_a per ottenere l'uscita entro il ±5% del valore finale.
• L'istante di massima sovraelongazione
  E' l'istante T_m in cui si verifica la massima sovraelongazione.

Per ottenere la funzione della risposta y(t) nel tempo calcolo l'antitrasformata

$$ y(t) = L^{-1}[ G(s) ] $$

$$ y(t) = L^{-1}[ \frac{ω^2_n}{s^2+2δω_ns+ω^2_n} ] $$

$$ y(t) = 1-Ae^{-δw_nt} sin(wt+φ) $$

dove $$ A=\frac{1}{\sqrt{1-δ^ω}} $$ $$ ω=ω_n \sqrt{1-δ^2} $$ $$ φ=\arctan \frac{\sqrt{1-δ^2}}{δ} = \arcsin \sqrt{1-δ^2} = \arccos δ $$

Nota. Il coefficiente di smorzamento ∂ determina l'ampiezza delle oscillazioni. Quanto più ∂ è alto, tanto più il segnale y(t) è vicino al valore finale.

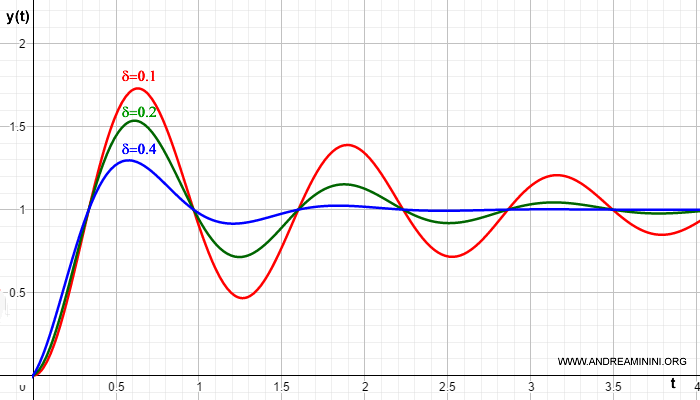
Inoltre, se il coefficiente di smorzamento ∂>0 la risposta converge al valore finale. Se ∂<0 la risposta diverge. Se ∂=0 la risposta è in oscillazione perpetua.

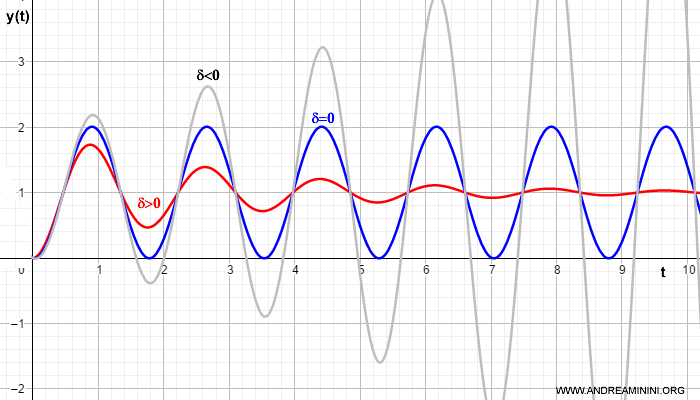
L'istante (t) di sovraelongazione si trova con la seguente formula

$$ t = \frac{nπ}{w_n \sqrt{1-∂^2}} $$

Dove n è il numero del picco da 1 in poi.

Considerando una pulsazione naturale pari a wn=3.14 ottengo il seguente grafico dei tempi di sovraelongazione

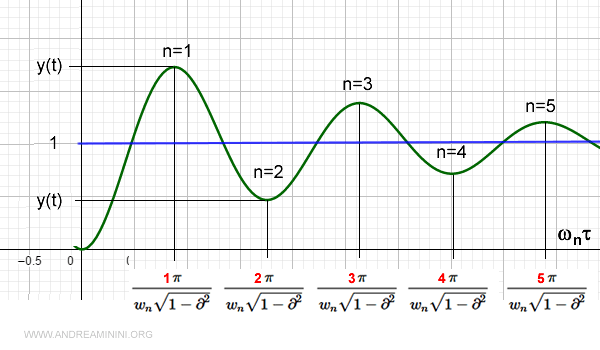
Sostituendo t nella formula che determina y(t) ottengo la funzione che determina la y(t)

$$ y(t) = 1 - (-1)^n e^{\frac{-nπ∂}{\sqrt{1-∂^2}}} $$

La percentuale della massima sovraelongazione è

$$ S = 100 \cdot e^{\frac{-π∂}{\sqrt{1-∂^2}}} $$

E così via