Equazione generale del sistema

L'equazione generale del sistema è una o più equazioni differenziali che spiegano un sistema lineare stazionario di ordine n

Ecco l'equazione del sistema nella sua forma generale

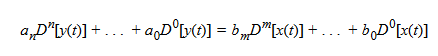
Posso scrivere la soluzione generale anche in forma compatta

$$ \sum_{i=0}^{n} a_i D^i[y] = \sum_{i=0}^{m} b_i D^i[x] $$

• a e b sono coefficienti costanti.
• l'indice n è detto ordine del sistema
• la funzione y(t) è l'uscita del sistema (effetto)
• la funzione x(t) è l'ingresso del sistema (causa) anche detto termine noto.

Nota. In genere si suppone che n≥m. In caso contrario la risposta del sistema avrebbe un'ampiezza infinita. Secondo il teorema di Cauchy il sistema è strettamente causale se m<n, nel caso limite m=n il sistema è causale ma non strettamente causale.

L'intervallo temporale

L'intervallo di variazione della variabile t è da 0 a T (estremo superiore) con T che può essere un numero finito oppure più infinito.

$$ x(t) , 0 \le t \le T $$

I numeri negativi del tempo non sono presi in considerazione perché qualsiasi fenomeno evolve in avanti nel tempo a partire dall'istante zero (presente).

Se l'estremo T non è specificato, si intende +∞.

Nota. Si suppone che la funzione di ingresso x(t) sia limitata e continua a tratti.

Le condizioni iniziali e il segnale di ingresso

Per trovare la soluzione dell'equazione differenziale devo conoscere

1. Le condizioni iniziali del sistema
   Si trovano ponendo la variabile t=0 delle derivate della variabile y(t) fino all'ordine n-1.
   $$ y(0), y'(0), ... , y^{n-1}(0) $$
2. Il segnale di ingresso x(t)
   L'equazione differenziale ammette una soluzione y(t).
   La soluzione y(t) è continua se m<n oppure è continua a tratta se m=n.

L'evoluzione libera e forzata

Per trovare la soluzione è utile analizzare separatamente la condizione iniziale e il segnale di ingresso.

• Evoluzione libera
  Per ipotesi suppongo nullo il segnale di ingresso per determinare la soluzione che soddisfa le condizioni iniziali y₀(t) e l'equazione differenziale omogenea associata con i segnali di ingresso x(t) a zero. $$ \begin{cases} y(0), y'(0), ... , y^{n-1}(0) \\ \\ \sum_{i=0}^{n} a_i D^i[y] = 0 \end{cases} $$

  Nota. In questo caso l'evoluzione del sistema y₀ dipende esclusivamente dalle condizioni iniziali ossia dai parametri che determinano lo stato iniziale del sistema.

• Evoluzione forzata
  Per ipotesi suppongo nulle le condizioni iniziali y(t) fino alla derivata di ordine n-1 per determinare la soluzione dell'equazione differenziale. $$ \begin{cases} y(0), y'(0), ... , y^{n-1}(0) = 0 \\ \\ \sum_{i=0}^{n} a_i D^i[y] = \sum_{i=0}^{m} b_i D^i[x] \end{cases} $$

  $$ Nota. In questo caso l'evoluzione del sistema y₁ dipende esclusivamente dai segnali di ingresso.

Una volta trovate le due soluzioni, sommo tra loro la funzione ottenuta dall'evoluzione libera e dall'evoluzione forzata.

$$ y(t) = y_0(t)+y_1(t) $$

In questo modo ottengo

$$ \sum_{i=0}^{n} a_i D^i[y_0] + \sum_{i=0}^{n} a_i D^i[y_1] = 0 + \sum_{i=0}^{m} b_i D^i[x] $$

Nota. La forma generale non comprende comunque tutti i casi possibili. Ad esempio, non considera i fenomeni propagatori causati da derivate parziali. Inoltre, la soluzione non è valida se i parametri cambiano in funzione del tempo ossia se il sistema non è stazionario.

E così via.