Gli angoli tra le rette
Due rette incidenti in un punto P formano quattro angoli con due coppie opposte di angoli di uguale ampiezza α e 1-α.
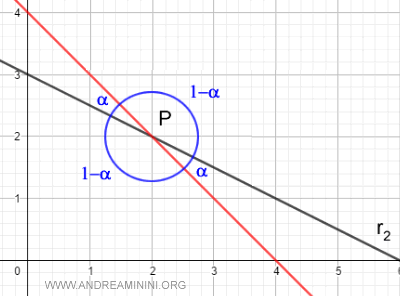
Se le rette sono parallele o coincidenti si pone per definizione l'angolo α=0 e 1-α=π.
Come calcolare l'ampiezza degli angoli
Per trovare l'ampiezza degli angoli devo conoscere le equazioni delle rette.
Vanno bene sia le equazioni parametriche che cartesiane.
Le equazioni parametriche
Dalle equazioni parametriche considero soltanto i vettori direttori.
$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} l_2 \\ m_2 \end{pmatrix} $$
Questi elementi sono sufficienti per calcolare il coseno dell'angolo usando la seguente formula.
$$ cos(\widehat{v_1v_2}) = \frac{ < v_1 , v_2 > }{ || v_1 || \cdot || v_2 || } $$
$$ cos(\widehat{v_1v_2}) = \frac{l_1l_2+m_1m_2}{\sqrt{l^2_1+m^2_1} \cdot \sqrt{l^2_2+m^2_2} } $$
Nota. E' il rapporto tra il prodotto scalare dei due vettori e il prodotto delle rispettive norme.
Le coppie di angoli hanno le seguenti ampiezze:
$$ \widehat{v_1v_2} $$
$$ π - \widehat{v_1v_2} $$
Esempio
In questo esempio ho le equazioni parametriche di due rette r1 e r2.
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 4 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ -2 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 3 \end{pmatrix} + t \cdot \begin{pmatrix} -8 \\ 4 \end{pmatrix} $$
La rappresentazione grafica è la seguente:
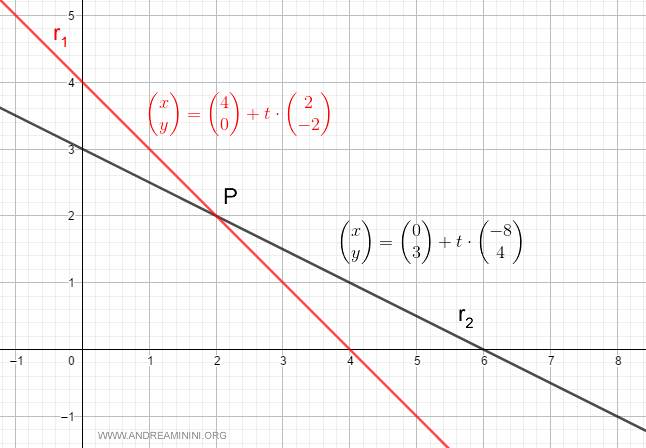
Le due rette si intersecano nel punto P dove si formano quattro angoli.
Per calcolare l'ampiezza degli angoli prendo come riferimento i vettori direttori delle due equazioni parametriche:
$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \end{pmatrix} $$
$$ v_2 = \begin{pmatrix} l_2 \\ m_2 \end{pmatrix} = \begin{pmatrix} -8 \\ 4 \end{pmatrix} $$
A questo punto uso la formula del coseno dei vettori direttori
$$ cos(\widehat{v_1v_2}) = \frac{l_1l_2+m_1m_2}{\sqrt{l^2_1+m^2_1} \cdot \sqrt{l^2_2+m^2_2} } $$
$$ cos(\widehat{v_1v_2}) = \frac{2 \cdot (-8) + (-2) \cdot 4}{\sqrt{2^2+(-2)^2} \cdot \sqrt{(-8)^2+4^2} } $$
$$ cos(\widehat{v_1v_2}) = \frac{-16 -8}{\sqrt{4+4} \cdot \sqrt{64+16} } $$
$$ cos(\widehat{v_1v_2}) = \frac{-24}{\pm \sqrt{8} \cdot \sqrt{80} } $$
$$ cos(\widehat{v_1v_2}) = \pm 0,94 $$
Attenzione. Il valore del coseno non è l'ampiezza dell'angolo. Per convertire il coseno nell'angolo equivalente che lo determina, occorre usare la funzione inversa del coseno ossia l'arcocoseno (acos).
Una volta capito che il coseno dell'angolo è uguale a 0,94 mi basta calcolare l'arcocoseno per ottenere i radianti dell'angolo.
$$ acos(0,94) = 0,34 rad $$
L'angolo α ha un'ampiezza di 0,34 radianti.
L'altro angolo ha un'ampiezza di π-α ossia 3,14 - 0,34 ossia 2,8 radianti.

Le equazioni cartesiane
Dalle equazioni cartesiane delle rette
$$ a_1 x + b_1 y + c_1 = 0 $$
$$ a_2 x + b_2 y + c_2 = 0 $$
prendo in considerazione soltanto i vettori normali
$$ n_1 = \begin{pmatrix} a_1 \\ b_1 \end{pmatrix} $$
$$ n_2 = \begin{pmatrix} a_2 \\ b_2 \end{pmatrix} $$
Il resto del procedimento di calcolo dell'ampiezza dell'angolo è simile a quello già visto per le equazioni parametriche.
$$ cos(\widehat{n_1n_2}) = \frac{ < n_1 , n_2 > }{ || n_1 || \cdot || n_2 || } $$
$$ cos(\widehat{n_1n_2}) = \frac{a_1a_2+b_1b_2}{\sqrt{a^2_1+b^2_1} \cdot \sqrt{a^2_2+b^2_2} } $$
Le coppie di angoli hanno le seguenti ampiezze:
$$ \widehat{v_1v_2} $$
$$ π - \widehat{v_1v_2} $$
Un esempio
Due rette sono rappresentate dalle seguenti equazioni cartesiane:
$$ x+y-4=0 $$
$$ \frac{1}{2}x+y-3=0 $$
La rappresentazione grafica sul diagramma cartesiano è la seguente:
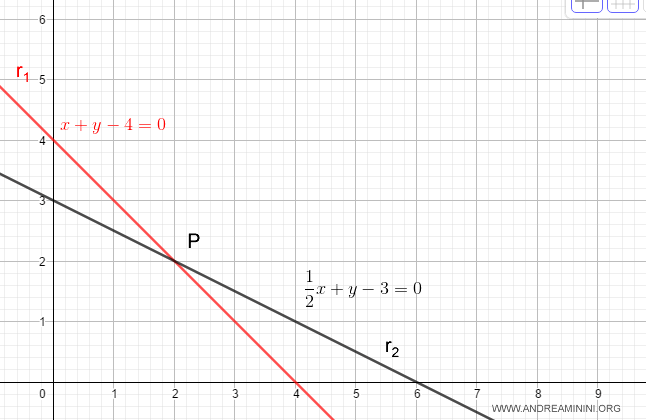
I vettori normali delle due rette sono
$$ n_1 = \begin{pmatrix} a_1 \\ b_1 \end{pmatrix} = \begin{pmatrix} 1 \\1 \end{pmatrix} $$
$$ n_2 = \begin{pmatrix} a_2 \\ b_2 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ 1 \end{pmatrix} $$
Ora, per calcolare l'ampiezza degli angoli applico la solita formula
$$ cos(\widehat{n_1n_2}) = \frac{ < n_1 , n_2 > }{ || n_1 || \cdot || n_2 || } $$
$$ cos(\widehat{n_1n_2}) = \frac{a_1a_2+b_1b_2}{\sqrt{a^2_1+b^2_1} \cdot \sqrt{a^2_2+b^2_2} } $$
$$ cos(\widehat{n_1n_2}) = \frac{1 \cdot \frac{1}{2} + 1 \cdot 1}{\sqrt{1^2+1^2} \cdot \sqrt{( \frac{1}{2})^2+1^2} } $$
$$ cos(\widehat{n_1n_2}) = \frac{ \frac{1}{2} + 1}{\sqrt{2} \cdot \sqrt{ \frac{1}{4}+1} } $$
$$ cos(\widehat{n_1n_2}) = \frac{ \frac{3}{2}}{\sqrt{2} \cdot \sqrt{ \frac{5}{4}} } $$
$$ cos(\widehat{n_1n_2}) = 0,94 $$
Nota. E' lo stesso risultato dell'esempio precedente perché le rette sono le stesse. In questo caso sono rappresentate con le equazioni cartesiane.
Una volta trovato il valore del coseno, per trovare l'ampiezza dell'angolo devo soltanto calcolare l'arcocoseno.
$$ acos(0,94) = 0,34 rad $$
L'angolo α ha un'ampiezza di 0,34 radianti.
L'altro angolo ha un'ampiezza di π-α ossia 3,14 - 0,34 ossia 2,8 radianti.
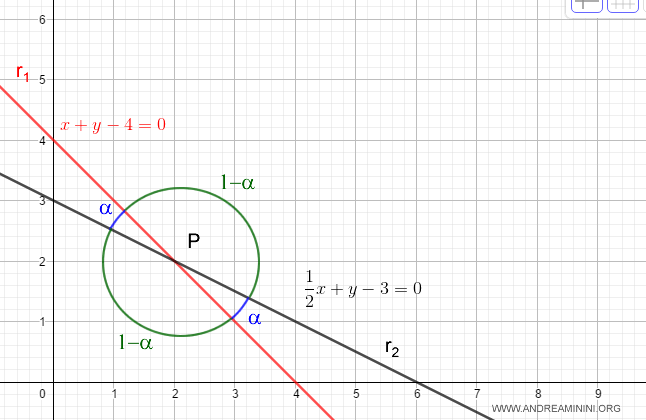
E così via.
