Funzione esponenziale complessa
La funzione esponenziale di un numero complesso $$ e^z $$ si calcola considerando il numero complesso z=x+iy dove i è l'unità immaginaria.
La funzione complessa di un numero approssima una serie di potenze.
$$ e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + ... $$
In questo caso z=x+iy è un numero complesso, composto da una parte reale (x) e una parte immaginaria (iy).
$$ e^z = e^{x+iy} $$
Per la regola della somma di un esponenziale equivale a
$$ e^z = e^{x+iy} = e^xe^{iy} $$
Dove il fattore ex è il modulo di un vettore che inizia dall'origine e la parte immaginaria y del numero complesso z è l'angolo del vettore.
$$ e^z = e^xe^{iy} = e^x \cdot ( \cos y + i \cdot \sin y) $$
Un esempio pratico
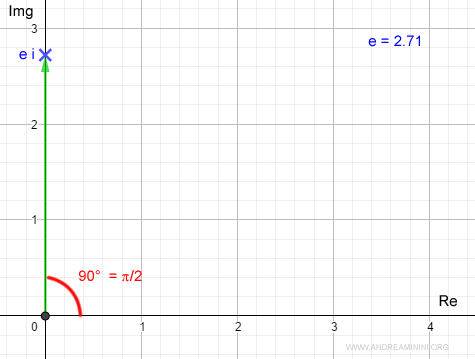
Esempio 1 (come calcolare l'esponenziale complesso)
Prendo in considerazione l'esponente complesso
$$ e^{1+\frac{π}{2}i} $$
Dove il numero complesso z=1+π/2.
La parte reale (Re) è 1 mentre la parte immaginaria (Img) del numero complesso è π/2.
Per calcolare il numero complesso scompongo l'esponenziale in reale e immaginario
$$ e^1 \cdot e^{\frac{π}{2}i} $$
Sapendo che il secondo esponenziale è l'angolo (argomento) lo scrivo in forma trigonometrica
$$ e^1 \cdot ( \cos \frac{π}{2} + i \cdot \sin \cos \frac{π}{2} ) $$
Calcolo il seno e il coseno di π/2 (ossia 90°)
$$ e^1 \cdot ( 0 + i \cdot 1 ) $$
Poi moltiplico considerando e1=e
$$ 0 + i \cdot e $$
Pertanto, l'esponenziale complesso ez del numero z=1+π/2i è 0+ei
Esempio 2 (funzione complessa)
Prendo in considerazione la funzione esponenziale complessa
$$ e^{1+2i} $$
L'esponente è un numero complesso z=x+yi ossia z=1+2i.
La parte reale del numero è x=1 e la parte immaginaria è y=2i.
La funzione complessa è approssimabile con la serie di potenze.
$$ e^z = 1 + z + \frac{z^2}{2!} + \frac{z^3}{3!} + ... $$
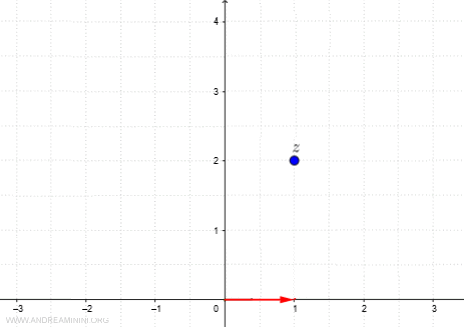
Il primo termine della serie è 1 ossia (1+0i).
La funzione parte dall'origine. Traccio il primo vettore della funzione tra (0,0i) e (1,0i).
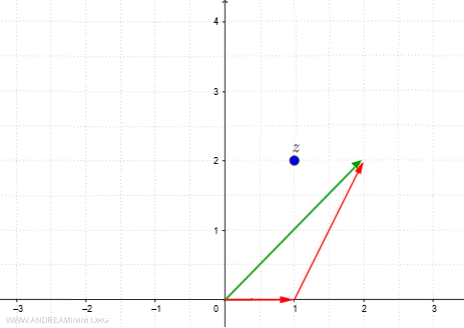
Il secondo termine della serie è z ossia z=1+2i.
Sommo 1+2i con 1+0i e ottengo 2+2i.
Il nuovo vettore che approssima la serie congiunge l'origine (0,0i) con (2,2i).
Il terzo termine della serie è z^2/2!
$$ \frac{z^2}{2!} = \frac{(1+2i)^2}{2} = \frac{1+4i+4i^2}{2} = \frac{1+4i-4}{2} = \frac{-3+4i}{2} $$
Sommo il nuovo termine alla serie precedente
$$ (1+0i) + (1+2i) + (\frac{-3+4i}{2}) = $$
$$ (2+2i) + (\frac{-3+4i}{2}) = $$
$$ \frac{4+4i-3+4i}{2} = $$
$$ \frac{1+8i}{2} = $$
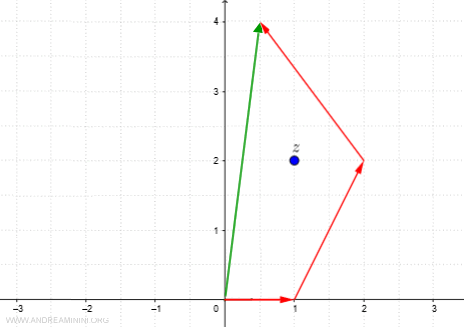
$$ \frac{1}{2} +4i $$
Il nuovo vettore coingiunge l'origine (0,0i) del piano di Gauss con il punto (1/2,4i)
Usando lo stesso metodo calcolo alcuni componenti successivi della funzione che approssima la serie di potenze.
Il risultato finale è il seguente.
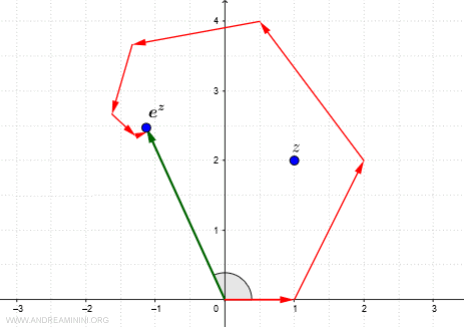
E così via.
