Anelli in algebra

Cosa sono gli anelli in algebra

Un anello è una struttura algebrica composta da un insieme e due operazioni binarie ( somma e prodotto ) che rispettano le proprietà dei numeri interi. $$ (S,+, \cdot) $$

Gli anelli sono studiati in algebra astratta nella teoria degli anelli.

Le proprietà degli anelli

Un anello deve rispettare le seguenti proprietà

• Proprietà commutativa dell'addizione
  $$ a+b=b+a $$
• Proprietà commutativa della moltiplicazione
  $$ a \cdot b=b \cdot a $$
• Proprietà associativa dell'addizione
  $$ (a+b)+c=a+(b+c) $$
• Proprietà associativa della moltiplicazione
  $$ (a \cdot b) \cdot c=a \cdot (b \cdot c) $$
• Proprietà distributiva della moltiplicazione rispetto all'addizione
  $$ a \cdot (b+c)=(a \cdot b)+(a \cdot c) $$ $$ (b+c) \cdot a =(a \cdot b)+(a \cdot c) $$

  Nota. Da questa proprietà si deduce che le operazioni di un anello non sono interscambiabili. L'ordine delle operazioni in un anello è essenziale. Un anello è un gruppo abeliano rispetto alla prima operazione. Rispetto alla seconda operazione non è necessario. Ad esempio (S,+,*) è un anello mentre (S,*,+) non lo è perché (S,*) non è un gruppo abeliano.

• Esistenza elemento neutro dell'addizione
  $$ a+0=0+a=a $$
• Esistenza elemento neutro della moltiplicazione
  $$ a \cdot 1=1 \cdot a=a $$

Esempi di anelli

Esempio 1

Un esempio di anello è l'insieme dei numeri interi Z con le operazioni di somma e prodotto.

$$ (Z,+,\cdot) $$

Esempio 2

L'insieme dei numeri reali R è un anello rispetto all'addizione e alla moltiplicazioni.

$$ (R,+,\cdot) $$

Esempio 3

L'insieme dei polinomi di grado n è un anello rispetto alle operazioni di somma e prodotto.

$$ (P[n],+,\cdot) $$

Esempio 4

L'insieme delle matrici quadrate di ordine n è un anello rispetto alle operazioni di somma e prodotto.

$$ (M[n],+,\cdot) $$

I sottoanelli

Un sottoanello è un sottoinsieme T di S con le stesse operazioni di (S,+,·) che rispetta tutte le proprietà dell'anello.

Esempio

L'insieme 2Z (numeri interi moltiplicati per due) è un sottoinsieme dell'insieme dei numeri interi Z .

Il sottoinsieme 2Z fa parte del sottoanello (2Z,+,·) perché rispetta le stesse proprietà dell'anello (Z,+,·).

Un sottoanello è detto ideale se per ogni elemento s di S e t di T, il prodotto st appartiene a T. $$ s \cdot t = t \cdot s \in T $$

Omomorfismo e isomorfismo di anelli

Un omomorfismo è un'applicazione f che mette in relazione due anelli R e R'. $$ f:R \rightarrow R' $$ che rispettano le stesse proprietà $$ f(a+b)= f(a)+f(b) $$ $$ f(a \cdot b)=f(a) \cdot f(b) $$ dove a e b sono elementi di R.

Se la corrispondenza è biunivoca si parla di isomorfismo.

$$ f:R \rightarrow R' $$ $$ f^{-1}:R' \rightarrow R $$

Esempio

Dato l'anello dei numeri interi (Z,+,·) un omomorfismo è la seguente applicazione

$$ f: a-b \in Z \rightarrow Z' $$

Questa applicazione mette in relazione l'insieme dei numeri interi Z e l'insieme delle differenze dei numeri interi Z'.

Anche (Z',+,·) è un anello.

Esempio 2

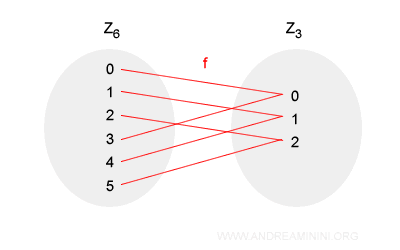
Un'applicazione collega l'anello Z₆ con l'anello Z₃ dei numeri interi secondo le proprietà dell'aritmetica modulare.

$$ f: Z_6 \rightarrow Z_3 $$

Quindi

$$ [x_6] = x + 6 k $$

$$ [x_3] = x + 3 k $$

Preso un [x₆] si ha

$$ f([x_6])= [x_3] $$

nel caso in cui

$$ [x_6] = x + 6 k $$

$$ [x_6] = x + 3 (2k) $$

La tavola dell'addizione e della moltiplicazione dell'anello (Z₆ ,+ ,·) è

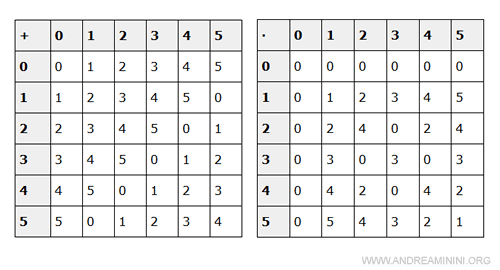
La tavola dell'addizione e della moltiplicazione dell'anello (Z₃ ,+ ,·) è

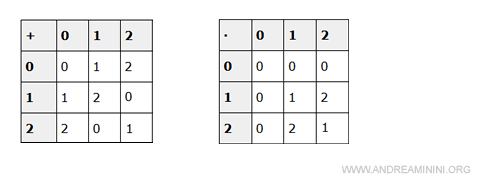
Devo dimostrare che è un omomorfismo.

$$ f([a]_6+[b]_6) = f([a]_6)+f([b]_6) = [a+b]_3$$

$$ f([a]_6 \cdot [b]_6) = f([a]_6) \cdot f([b]_6) = [a \cdot b]_3 $$

Ad esempio, prendo gli elementi a=4 e b=4 in x₆

$$ f(4+4)_6 = f(2)_6 = [2]_3 $$

$$ f(4)_6+f(4)_6 = [1+1]_3 = [2]_3 $$

La prima proprietà è dimostrata.

$$ f(4 \cdot 4)_6 = f(4)_6 = [1]_3 $$

$$ f(4)_6 \cdot f(4)_6 = [1 \cdot 1]_3 = [1]_3 $$

Anche la seconda proprietà degli omomorfismi è dimostrata.

E' un omomorfismo di anelli.

Il nucleo dell'omomorfismo di anelli

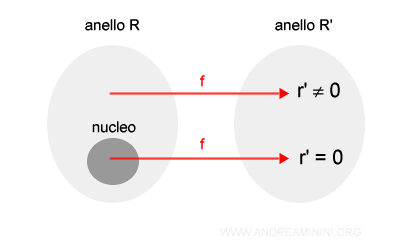
Dato un omomorfismo f tra due anelli R e R', il nucleo è l'insieme degli elementi di R tale che f()=0_R'. $$ f(r) = 0_{R'} \forall r \in R $$ E' anche indicato come ker(f).

In pratica, il nucleo è un sottoinsieme di R con le controimmagini di 0_R'.

Esempio

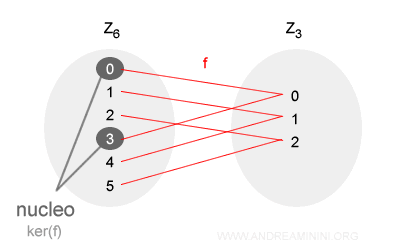
Nell'esempio precedente dell'omomorfismo f:Z₆→ Z₃ il nucleo è il sottoinsieme di Z₆ con gli elementi { [0]₆, [3]₆ }

La relazione tra il nucleo e il sottoinsieme ideale

C'è uno stretto legame tra il sottoanello ideale I e il nucleo di un isomorfismo.

Il nucleo dell'omomorfismo f:R →R' è un sottoanello ideale di R.

Ad esempio, tralasciando il caso banale dello zero, nell'esempio precedente si ha

$$ 3 \cdot 0 = 0 \\ 3 \cdot 1 = 3 \\ 3 \cdot 2 = 0 \\ 3 \cdot 3 = 3 \\ 3 \cdot 4 = 0 \\ 3 \cdot 5 = 0 $$

Pertanto, il nucleo ker(f) è un sottoinsieme ideale di Z₃.

La relazione è anche inversa

Pertanto, ogni sottoinsieme ideale è il nucleo di un isomorfismo.

Per ogni sottoinsieme ideale I esiste una relazione di equivalenza θ tale che $$ a \: θ \: b \Leftrightarrow a-b \in I \:\:\: \forall a,b \: \in R $$

Differenza tra anello e campo

Un anello è un gruppo abeliano rispetto alla prima operazione ( addizione ) ma non rispetto alla seconda ( moltiplicazione ).

Il campo è un anello che è un gruppo abeliano rispetto a entrambe le operazioni.

Esempio 1 ( anello )

L'anello dei numeri interi (Z,+,*) è un gruppo abeliano rispetto all'addizione.

$$ 7 + (-7) = 0 $$

Viceversa, non è un gruppo abeliano rispetto alla moltiplicazione perché non esiste un inverso di un numero intero n tale che

$$ n * n^{-1} = 1 $$

Ad esempio, il numero 7 non ha un inverso nell'insieme nei numeri interi. Non esiste 1/7.

Quindi, non è un gruppo abeliano rispetto alla moltiplicazione.

Esempio 2 ( campo )

L'anello dei numeri frazionari (Q,+,·) è un gruppo abeliano rispetto all'addizione e alla moltiplicazione.

$$ 7 + (-7) = 0 $$

$$ 7 * 7^{-1} = 1 $$

Entrambe le operazioni danno come risultato l'elemento neutro dell'operazione.

E' quindi un campo.

Nota. In un campo si possono fare molte più operazioni rispetto a un anello. Ad esempio, si possono dividere due numeri.

Osservazioni

Alcune osservazioni sugli anelli

• Anello commutativo
  Un anello è detto commutativo se anche la seconda operazione rispetta la proprietà commutativa
• Anello con unità
  Un anello è detto anello con unità se anche la seconda operazione ha un elemento neutro
• Anello di divisione (o corpo)
  Un anello è detto anello di divisione (o corpo) se l'insieme S privato dell'elemento neutro della somma (primma operazione) forma un gruppo rispetto alla seconda operazione $$ ( S-{0}, \cdot ) $$
• Campo
  Se il corpo è commutativo si parla di campo. Quindi, il campo è un anello in cui l'insieme senza l'elemento neutro della somma (prima operazione) forma un gruppo commutativo rispetto alla moltiplicazione (seconda operazione)

E così via.