Il minimo e massimo di una funzione

Secondo il Teorema di Fermat, una funzione definita in un intervallo [a,b] ha un minimo o un massimo locale nel punto x₀, se la derivata prima è uguale a zero in x₀. $$ f'(x_0)=0 $$

Pertanto, per cercare un minimo o un massimo, devo

1. calcolare la derivata prima della funzione f(x)
2. trovare i punti in cui la derivata prima è nulla f'(x)=0

Questo metodo è applicabile soltanto se la funzione è derivabile in [a,b].

Una volta trovati i punti in cui la derivata prima è nulla, ad esempio x₀, devo capire se si tratti di un minimo o di un massimo.

Come capire se è un massimo o un minimo

Posso seguire diverse strade alternative.

1. Analizzare la crescenza / decrescenza della derivata prima f'(x) nell'intorno di x₀.
   • Se la derivata prima è crescente, si tratta di un minimo locale.
   • Se la derivata prima è decrescente, si tratta di un massimo locale.
2. Calcolare la derivata seconda f"(x) nell'intorno di x₀.
   • Se la derivata seconda è maggiore o uguale a zero, è un minimo locale. $$ f"(x_0) \ge 0 \Leftrightarrow minimo $$
   • Se la derivata seconda è minore o uguale a zero, è un massimo locale. $$ f"(x_0) \le 0 \Leftrightarrow massimo $$

Nota Il metodo delle derivate si può generalizzare alle derivate pari di qualsiasi ordine k con le precedenti derivate nulle. $$ f^{(k)} \ne 0 \:\:\: k=pari $$ $$ f^{(1)} = f^{(2)} = ... = f^{(k-1)} = 0 $$ E' quindi molto utile per lo studio e l'analisi matematica di una funzione. Ha però il limite di essere applicabile soltanto se la funzione è continua e derivabile in x₀.

I due metodi precedenti sono del tutto equivalenti tra loro per il criterio di monotonia.

• Se la funzione derivata prima f'(x) è crescente nell'intorno x₀, allora la derivata seconda è sicuramente maggiore o uguale a zero. $$ f'(x) \:\: crescente \:\: \Leftrightarrow \:\: f"(x_0) \ge 0 $$
• Se la funzione derivata prima f'(x) è decrescente nell'intorno x₀, allora la derivata seconda è sicuramente minore o uguale a zero. $$ f'(x) \:\: decrescente \:\: \Leftrightarrow \:\: f"(x_0) \le 0 $$

Un esempio pratico

Devo trovare i punti di massimo / minimo della funzione

$$ f(x)=x^2 $$

Calcolo la derivata prima della funzione

$$ f'(x)=2x $$

Poi analizzo in quali radici si annulla

La derivata prima è uguale a zero solo nel punto x=0.

$$ x=0 \rightarrow f'(0)=0 $$

A questo punto calcolo la derivata seconda, ossia la derivata della derivata prima.

$$ f"(x)=2 $$

E infine studio il segno della derivata seconda nel punto x=0

$$ f"(0)=2 \ge 0 $$

La derivata seconda è maggiore di zero, quindi si tratta di un minimo.

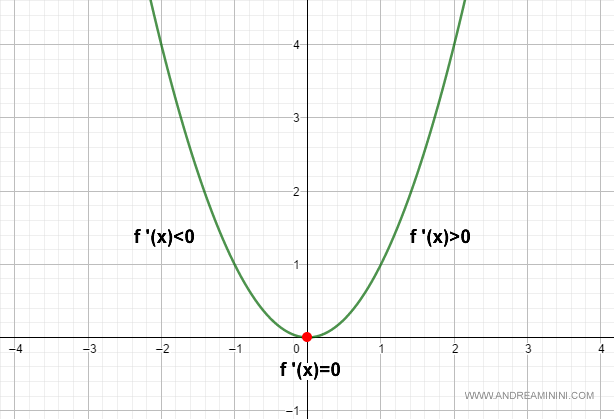
Dimostrazione

Una funzione è definita e continua in (a,b)

Se nel punto x₀∈(a,b) la derivata prima è nulla

$$ f'(x_0)=0 $$

Secondo il teorema di Femat nel punto x₀ la funzione f(x) potrebbe avere un minimo o un massimo.

Nota. Non è però detto che ci sia un minimo o un massimo Potrebbe anche esserci un flesso.

Se la derivata seconda in x₀ è positiva

$$ f"(x_0) > 0 $$

Essendo una funzione continua, secondo il teorema della permanenza del segno deve esistere un intorno (x-δ,x+δ) in cui f"(x)>0.

Pertanto, in questo intorno la funzione prima f'(x) è crescente e la funzione f(x) è convessa.

Se la funzione è convessa, la retta tangente in x₀ è sempre al di sotto della funzione f(x).

$$ f(x) \ge f(x_0)+f'(x_0)(x-x_0) $$

Essendo f'(x₀)=0

$$ f(x) \ge f(x_0) $$

Questo dimostra che si tratti di un punto minimo.

Nota. Il punto di massimo si dimostra in modo analogo, partendo dall'ipotesi che la derivata seconda in x₀ è negativa.

E così via.