Il criterio di Nyquist
Il criterio di Nyquist mi consente di studiare la stabilità di un sistema dinamico in retroazione negativa a ciclo chiuso W(s), osservando il diagramma di Nyquist del sistema ad anello aperto G(s).
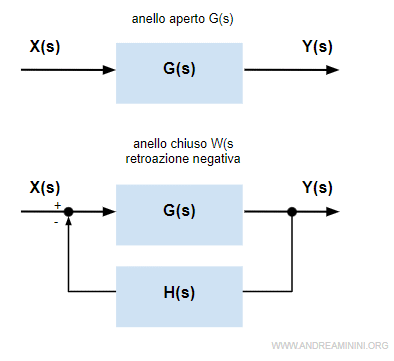
Cosa afferma il criterio di Nyquist
- il sistema in retroazione ad anello chiuso W(s) è asintoticamente stabile se
- se il sistema ad anello aperto G(s) è asintoticamente stabile e
- la funzione di guadagno di anello G(s) ha tutti i poli a parte reale negativa
- il diagramma polare della G(s) non circonda, né tocca il punto critico -1+j·0.
- oppure in senso più generale con G(s) stabile o instabile se
- la funzione di guadagno di anello G(s) non ha poli immaginari
- il diagramma polare della G(s) circonda il punto critico -1+j·0 in senso antiorario N tante volte quanti sono i poli a parte reale nG della G(s) $$ N = n_G $$
Nel criterio di Nyquist il sistema può avere eventualmente polo nell'origine semplice o doppio.
A cosa serve?
Il criterio di Nyquist è uno strumento grafico che permette lo studio della stabilità dei sistemi a retroazione.
E' abbastanza semplice da usare per la sua natura grafica. In particolar modo se il sistema non ha zeri o poli immaginari, ad eccezione di un polo semplice o doppio nell'origine.
Quando non si può applicare il criterio di Nyquist? Il criterio di Nyquist non è applicabile se il diagramma di Nyquist passa esattamente per il punto critico (-1,0). Questo caso non è ben definito.
Come applicare il criterio di Nyquist
Prendo in considerazione un sistema ad anello aperto
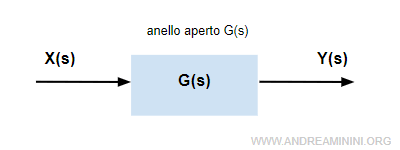
la cui funzione di trasferimento G(s) è
$$ G(s) = \frac{N(s) }{D(s)} $$
Dove N è il polinomio al numeratore e D è il polinomio al denominatore.
Il corrispettivo sistema in retroazione negativa ad anello chiuso è
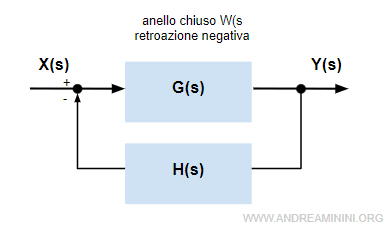
con la seguente funzione di trasferimento W(s)
$$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$
Il criterio di Nyquist mi permette di capire se la W(s) è stabile tramite l'analisi della G(s).
Per ipotesi la funzione G(s) è asintoticamente stabile per ω→∞ con s=jω.
$$ \lim_{ω→∞} G(jω) = K $$
Individuo il numero dei poli reali instabili nG della G(s) risolvendo l'equazione del polinomio al denominatore D=0.
Un polo reale conferisce instabilità soltanto se è positivo.
Esempio. Se la funzione di trasferimento ad anello aperto è $$ G(s) = \frac{5}{1+s} $$ i poli sono le soluzioni dell'equazione $$ 1+s = 0 $$ In questo caso c'è soltanto una soluzione (polo) negativa ossia s=-1. Quindi non ci sono poli instabili a parte reale positiva.
Poi disegno il diagramma di Nyquist della funzione ad anello aperto G(s) per le pulsazioni ω da -∞ a +∞.
Esempio. Nel caso della funzione di trasferimento ad anello aperto è $$ G(s) = \frac{5}{1+s} $$ il diagramma di Nyquist è il seguente:
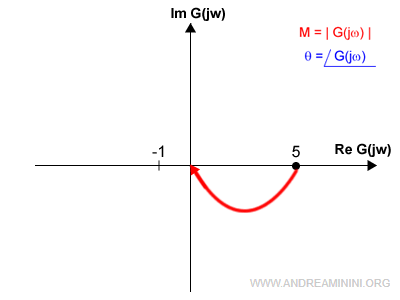
Per ottenere il disegno completo per ω→-∞ è sufficiente ribaltare il grafico rispetto all'asse reale.
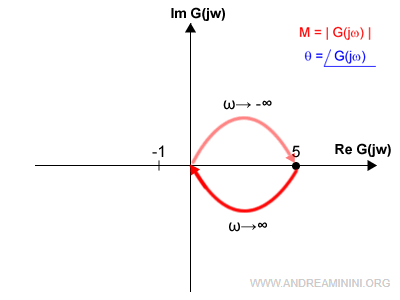
Il numero dei giri N compiuti dal vettore G(jω) nel percorso delle pulsazioni ∞ da -∞ a +∞ intorno al punto (-1,0) detto punto critico di Nyquist al variare della pulsazione ω sono pari alla differenza tra il numero dei poli reali positivi (instabili) n di G(jω) e W(jω).
$$ N = n_G - n_W $$
Le variabili nG e NW sono sicuramente numeri interi non negativi.
Il numero dei giri N può, invece, essere anche negativo perché la rotazione può avvenire in senso orario o antiorario.
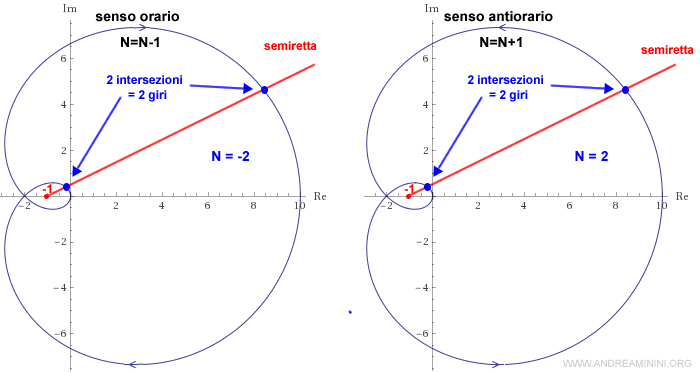
Nota. I giri in senso orario sono conteggiati come negativi. Inoltre, il numero N dei giri è ben definito, ossia definito senza ambiguità, se il diagramma di Nyquist non passa per il punto (-1,0).
Pertanto, conoscendo il numero dei giri in senso orario N e i poli instabili nG della G(jw) posso determinare algebricamente i poli instabili nW della W(jw) senza doverli calcolare.
$$ n_w = n_G - N $$
Se nW=0 allora il sistema a retroazione in catena chiusa è stabile.
Viceversa, se nW>0 il sistema a retroazione è instabile.
Esempio. La funzione di trasferimento ad anello aperto è $$ G(s) = \frac{5}{1+s} $$ ha nG=0 poli positivi e il diagramma di Nyquist compie N=0 giri intorno al punto (-1,0).

In base a questi due dati posso calcolare il numero dei poli instabili della funzione di trasferimento a retroazione ad anello chiuso $$ N = n_G - n_w $$ $$ 0 = 0 - n_w $$ $$ n_w = 0 $$ Non ci sono poli instabili nella funzione di trasferimento ad anello chiuso. Quindi, il sistema a retroazione negativa è stabile.
Un esempio pratico
Prendo in considerazione il sistema in anello aperto
$$ G(s) = \frac{90}{s^2+9s+18} $$
Il sistema in anello aperto è asintoticamente stabile per le pulsazioni ω→∞ dove s=jω.
$$ \lim_{ω→∞} G(jω) $$
$$ \lim_{ω→∞} \frac{90}{jω^2+9jω+18} = K = 0 $$
Inoltre, la funzione non ha poli a parte reale positiva (ossia instabili) e nessun polo nell'origine.
$$ n_G=0 $$
Nota. L'equazione al determinante $$ s^2+9s+18=0 $$ ha le soluzioni $$ \frac{ -9 ± \sqrt{81-72} }{2} = \frac{-9±3}{2} = \begin{cases} s= -3 \\ s=-6 \end{cases} $$ Quindi ci sono due poli negativi p1=-3 e p2=-6. Nessun polo a parte reale positiva.
A questo punto procedo con la costruzione del diagramma di Nyquist della G(s).
La funzione G(s) ha zero poli nell'origine (h=0).
Per ω→0 la funzione G(s) converge a 90/18=5.
$$ \lim_{ω \rightarrow 0^+} \frac{90}{jω^2+9jω+18} = \frac{90}{18} = 5 $$
Quindi, il diagramma di Nyquist comincia nell'asse reale positivo (K=5) nel punto (5,0) e per una regola generale di tracciamento abbandona l'asse reale in modo ortogonale.
Per ω→∞ la funzione G(s) converge a zero ossia all'origine del piano di Gauss.
$$ \lim_{ω \rightarrow \infty} \frac{90}{jω^2+9jω+18} = \frac{90}{18} = 0 $$
Poiché il numeratore K'=90>0, la fase di arrivo è -(n-m)π
Dove n è il grado del polinomio al denominatore (n=2) e m il grado del polinomio al numeratore (m=0) della funzione G(s).
$$ φ(∞) = -(2-0)π = -2π $$
Quindi la fase del punto finale è -2π ossia -180°.
In base a questi dati il diagramma di Nyquist della funzione è il seguente:
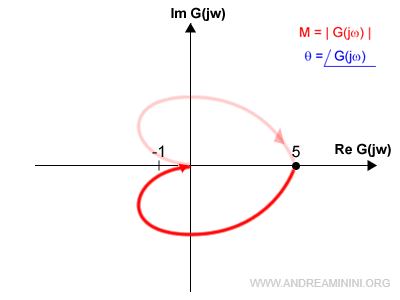
Nota. Una volta costruito il diagramma per le pulsazioni ω→∞ lo ribalto sull'asse reale per ottenere il grafico per ω→-∞.
A questo punto posso applicare il criterio di Nyquist per studiare la stabilità del sistema a retroazione W(s).
Il diagramma di Nyquist della G(s) non circonda il punto (-1,0).
Pertanto N=0.
$$ N = n_w-n_G $$
$$ 0 = n_w-n_G $$
Sapendo che anche i poli positivi della G(s) sono nG=0.
$$ 0 = n_w - 0 $$
Deduco che non ci sono poli positivi nw=0 nella W(s) ossia della funzione di trasferimento W(s) del sistema a retroazione negativa.
$$ n_w = 0 $$
Pertanto, il sistema a retroazione negativa (anello chiuso) è stabile.
Verifica. Per una verifica la funzione di trasferimento del sistema con retroazione ad anello chiuso è $$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$ La funzione di guadagno di anello è la seguente $$ L(s) = G(s) \cdot H(s) = \frac{90}{s^2+9s+18} \:\:\: con \: H(s)=1 $$ Il sistema è stabile se il denominatore 1+L(s) non ha poli positivi. $$ 1+L(s)=0 $$ $$ 1+ \frac{90}{s^2+9s+18} =0 $$ $$ \frac{s^2+9s+18+90}{s^2+9s+18} =0 $$ $$ s^2+9s+108 =0 $$ L'equazione si annulla per $$ \frac{-9±\sqrt{81-4 \cdot 108} }{2} = \frac{-9±\sqrt{-351} }{2} = \frac{-9±18.7j }{2} = -4.5±9.4j $$ La funzione W(s) non ha poli nell'asse reale positivo. Il sistema è stabile.
Esempio 2
Questo sistema ad anello aperto non ha poli reali positivi
$$ G(s) = \frac{10}{(1+2s)(1+3s)} $$
ed è asintoticamente stabile per ω→∞ con s=jω
$$ \lim_{ω \rightarrow \infty } \frac{10}{(1+2jω)(1+3jω)} = 0$$
Il diagramma di Nyquist del sistema G(s) è il seguente
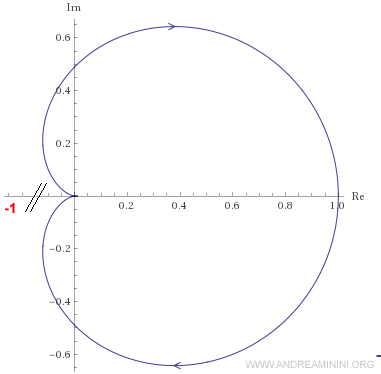
Poiché il diagramma non circonda il punto critico di Nyquist (-1,0) e il sistema G(s) è asintoticamente stabile, anche il sistema a retroazione ad anello chiuso W(s) è stabile.
$$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$
Esempio 3
La funzione ad anello aperto è
$$ G(s) = \frac{2(s+10)}{(s+1)^3} $$
La funzione ha un solo polo reale negativo s=-1 e zero poli positivi a parte reale.
$$ n_G=2 $$
Il diagramma di Nyquist della G(s) è il seguente
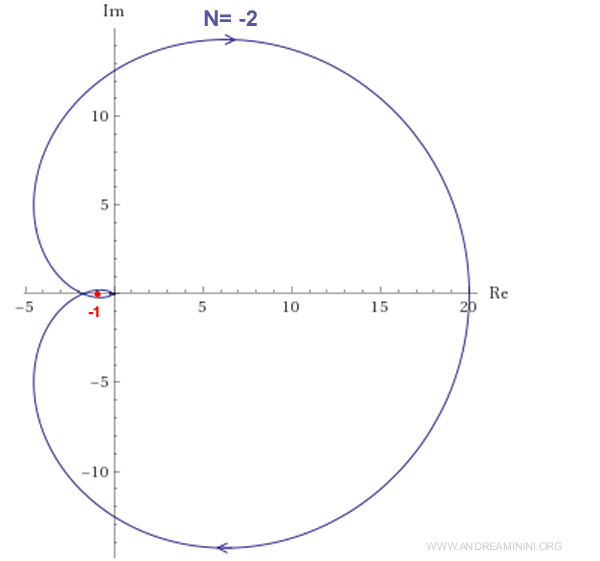
Il diagramma compie due giri in senso orario intorno al punto critico (-1,0). Quindi, N=-2.
$$ N = n_G - n_W $$
Quindi, sapendo che N=-2 e nG=0
$$ -2 = 0 - n_W $$
si può capire che il sistema a retroazione negativa a ciclo chiuso ha due poli reali nW=2.
$$ n_W = 2 $$
Pertanto, il sistema a ciclo chiuso W(s) della G(s) è instabile.
$$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$
La differenza tra i sistemi di tipo 0, 1 e 2
Nell'applicazione del criterio di Nyquist devo fare attenzione al tipo di sistema.
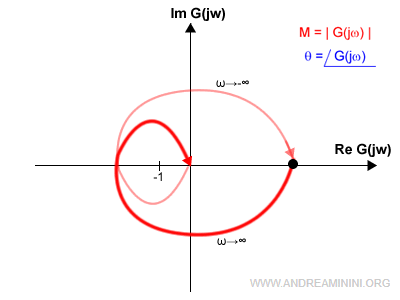
I sistemi di tipo 0
I sistemi di tipo 0 non hanno poli nell'origine.
Sono i più semplici da analizzare perché il diagramma di Nyquist è una curva chiusa.
Non ci sono considerazioni ulteriori da fare.
I sistemi di tipo 1
I sistemi di tipo 1 hanno un polo semplice nell'origine.
Sono più complessi da studiare perché il diagramma ha dei rami all'infinito e la curva non è chiusa.
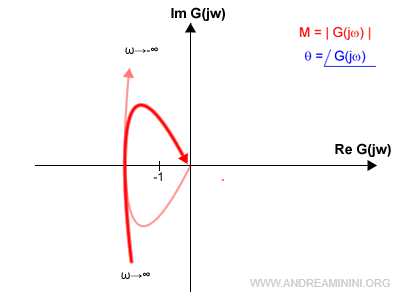
In questo caso devo chiudere la curva con una semicirconferenza in senso orario.
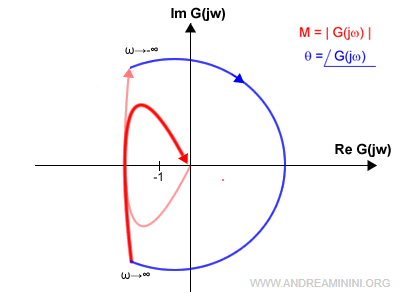
I sistemi di tipo 2
I sistemi di tipo 1 hanno un polo doppio nell'origine.
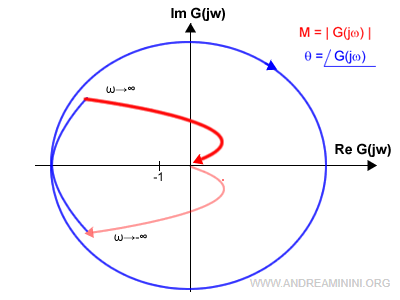
Anche i sistemi di tipo 2 presentano un diagramma ha dei rami all'infinito e la curva non è chiusa.
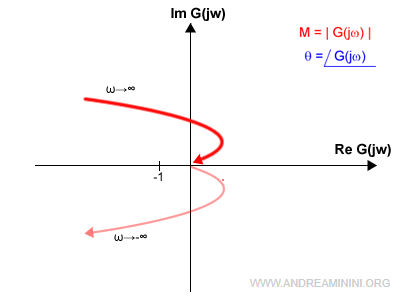
A differenza dei sistemi di tipo 1, in quelli di tipo 2 devo chiudere la curva con una circonferenza percorsa in senso orario.
I sistemi a stabilità condizionata
Un sistema a retroazione negativa è detto a stabilità condizionata se è stabile per alcuni valori della costante K e instabile per altri.
Esempio
Questo sistema ad anello aperto ha nG=2 poli reali positivi (p1=1/2 e p2=1/3) se K=10.
$$ G(s) = \frac{K(1+s)}{(1-2s)(1-3s)} $$
ed è asintoticamente stabile per ω→∞ con s=jω
$$ \lim_{ω \rightarrow \infty \frac{10(1+s)}{(1-2s)(1-3s)}} = 0 $$
Il diagramma di Nyquist del sistema ad anello aperto G(s) è il seguente
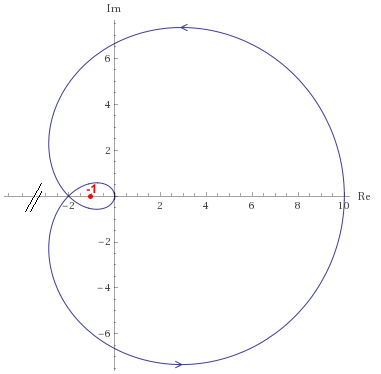
Poiché il diagramma circonda due volte in senso antiorario il punto critico di Nyquist (-1,0) e il sistema G(s) è asintoticamente stabile, anche il sistema a retroazione ad anello chiuso W(s) è stabile.
$$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$
Tuttavia, per altri valori inferiori di K il sistema diventa instabile.
Ad esempio, se K=5 la funzione G(s) ha sempre due poli reali positivi (p1=1/2 e p2=1/3) .
$$ G(s) = \frac{K(1+s)}{(1-2s)(1-3s)} $$
ed è asintoticamente stabile
$$ \lim_{ω \rightarrow \infty \frac{5(1+s)}{(1-2s)(1-3s)}} = 0 $$
In questo caso però il diagramma di Nyquist non circonda il punto critico (-1,0) nemmeno una volta N=0.
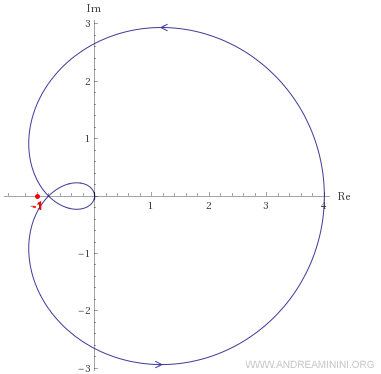
Quindi il sistema a retroazione W(s) ad anello chiuso ha due poli reali nW=nG-N=2 ed è instabile.
$$ W(s) = \frac{G(s)}{1+G(s)H(s)} $$
E' un esempio pratico di sistema a stabilità condizionata.
E così via.
