La coda M/M/1
La coda M/M/1 è il più semplice sistema a coda markoviano.
Secondo la notazione di Kendal, in una coda M/M/1 i processi di arrivo e di servizio sono distribuiti in modo esponenziale (M) ed esiste un solo servitore disponibile (1).
Non essendo definito nulla, lo spazio di accodamento e il numero dei clienti sono illimitati.
Questo sistema si può rappresentare con una catena di Markov nascita-morte in cui λ è il tasso di arrivo (nascita) e μ è il tasso di servizio (morte).
Ecco il diagramma delle transizioni di stato di una semplice coda.
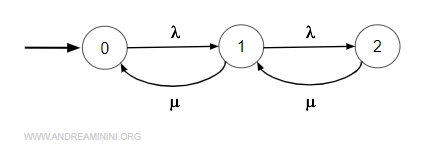
L'equazione della generica probabilità di stato a regime è
$$ π_j = ( \frac{λ}{μ} )^h \cdot π_0 $$
Dove π0 è la probabilità di stato iniziale.
$$ π_0 = \frac{1}{1 + \sum_{j=1}^{∞} ( \frac{λ}{μ} )^h } $$
La coda è stabile se il coefficiente di carico è minore di 1.
$$ δ = \frac{λ}{μ} < 1 $$
Se il sistema è stabile, la produttività è uguale a λ e la probabilità di stato iniziale a regime è
$$ π_0 = 1 - δ $$
Nota. Quest'ultima formula calcola la probabilità di non ricevere nessun cliente.
La lunghezza media della coda è
$$ x = \frac{δ}{1-δ} = \frac{λ}{μ-λ} $$
Sapendo che il tempo di permanenza dei clienti è
$$ o = \frac{x}{λ} $$
Usando la legge di Little dalla lunghezza della coda si ricava il tempo di permanenza nel sistema
$$ o = \frac{x}{λ} = \frac{1}{μ-λ} $$
Il tempo di permanenza nel sistema è la somma del tempo medio di attesa in coda (oc) e del tempo medio di servizio (os).
$$ o = o_c+o_s $$
Quindi, il tempo medio in coda è
$$ o_c = o-o_s $$
$$ o_c = \frac{x}{λ} = \frac{1}{μ-λ}-o_s =\frac{λ}{μ(μ-λ)} = \frac{δ}{μ(1-δ)} $$
Il numero medio di persone in coda è
$$ x_c = λ \cdot o_c = λ \cdot \frac{λ}{μ(μ-λ)} = \frac{λ^2}{μ(μ-λ)}= \frac{δ^2}{(1-δ)} $$
Un esempio pratico
Uno studio professionale riceve 4 clienti in 8 ore giornaliere.
$$ λ = \frac{4}{8} = \frac{1}{2} $$
Gli arrivi sono distribuiti secondo la distribuzione esponenziale di Poisson.
Ogni cliente richiede 1,5 ore di servizio (ossia 3/2).
$$ \frac{1}{μ} = \frac{3}{2} $$
Calcolo il coefficiente di carico per vedere se la coda è stabile
$$ δ = \frac{λ}{μ} = \frac{\frac{1}{2}}{\frac{2}{3}} = \frac{1}{2} \cdot \frac{3}{2} = \frac{3}{4} < 1 $$
Il coefficiente di carico è minore di 1.
Pertanto, la coda è stabile e la probabilità di stato iniziale di non ricevere nessun cliente nella giornata è
$$ π_0 = 1 - δ = 1 - \frac{3}{4} = \frac{1}{4} $$
La lunghezza media della coda è di 3 clienti
$$ x = \frac{δ}{1-δ} = \frac{\frac{3}{4}}{\frac{1}{4}} = \frac{3}{4} \cdot \frac{4}{1} = 3$$
Il tempo di permanenza nel sistema è di 6 ore
$$ o = \frac{x}{λ} = \frac{1}{μ-λ} = \frac{1}{\frac{2}{3}-\frac{1}{2}} = \frac{1}{\frac{4-3}{6}} == \frac{1}{\frac{1}{6}} = 6 $$
Il tempo in coda è di 4.5 ore
$$ o_c = \frac{x}{λ} = \frac{1}{μ-λ}-o_s = 6 - \frac{3}{2} = \frac{9}{2} = 4.5 $$
Il numero medio di persone in coda è
$$ x_c = λ \cdot o_c = \frac{1}{2} \cdot \frac{9}{2} = \frac{9}{4} = 2.25 $$
E così via
