La vivezza strutturale della rete
Una rete è strutturalmente viva se esiste una marcatura iniziale M0 in cui la rete marcata <N,M0> è viva.
La viviezza strutturale riprende la proprietà di viviezza comportamentale e la verifica in almeno una marcatura iniziale della rete.
Nella viviezza comportamentale, invece, la proprietà viene verificata soltanto per la marcatura iniziale predefinita della rete.
Nota. Dal punto di vista comportamentale una rete è detta rete viva se tutte le transizioni della rete possono essere abilitate e scattare a partire da qualsiasi marcatura raggiungibile della rete.
Come capire se una rete è strutturalmente viva
Posso verificarlo tramite i vettori P-decrescenti.
Una rete P/T è strutturalmente viva se NON esiste un P-vettore decrescente e non inviariante x, tale che $$ x \cdot C < 0 $$
Se il vettore x esiste, la rete è detta strutturalmente morta.
Nota. In questo caso devo prendere in considerazione soltanto i P-vettori strettamente decrescenti. Non devo considerare i P-vettori invarianti.
Un esempio pratico
Prendo in considerazione una rete con tre posti e tre transizioni
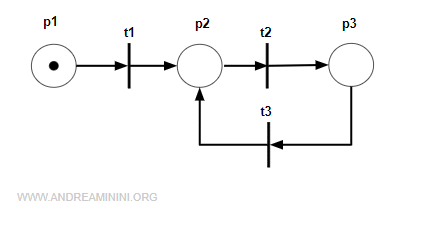
La matrice di incidenza della rete è
$$ C = \begin{pmatrix} -1 & 0 & 0 \\ 1 & -1 & 1 \\ 0 & 1 & -1 \end{pmatrix} $$
Per stabilire la viviezza della rete non deve esistere un vettore x $$
$$ x \cdot C < 0 $$
Verifico i possibili x vettori della rete
$$ [1,1,1] \cdot C = [0,0,0] \:\:\: P-invariante $$
$$ [1,1,0] \cdot C = [0, -1,1] \:\:\:$$
$$ [1,0,1] \cdot C = [-1,1,-1] \:\:\:$$
$$ [0,1,1] \cdot C = [1,0,0] \:\:\: P-crescente $$
$$ [1,0,0] \cdot C = [-1,0,0] \:\:\: P-decrescente $$
$$ [0,1,0] \cdot C = [1,-1,1] \:\:\: $$
$$ [0,0,1] \cdot C = [0,1,-1] \:\:\: $$
In questo caso esiste un vettore x=[1 0 0] P-decrescente e non invariante
Pertanto, la rete è strutturalmente morta.
Nota. La transizione t1 è morta a partire dalle marcature iniziali [0 0 1], [0 1 0] e altre. A partire da queste marcature non esiste una sequenza in grado di attivare la transizione t1.
E così via.
