La formula di Bode
La formula di Bode mi permette di disegnare il diagramma della fase a partire dal diagramma delle ampiezze. $$ β_c = \frac{1}{π} \int_{-∞}^{+∞} \frac{d \: α}{d \: u} \ln cotanh | \frac{u}{2}| du $$ dove $$ α = \ln | G(jω) | $$ $$ u = \ln \frac{ω}{ω_c} = \ln ω - \ln ω_c $$
Se la funzione di trasferimento è stabile e a fase minima, si verifica una correlazione tra la pendenza del diagramma delle ampiezze (a) e il diagramma della fase (b) nell'intorno di una pulsazione (w).
Nota. Una funzione razionale fratta è stabile e a fase minima se non ha poli e zeri nel semipiano destro del piano s (Re>0).
La formula di Bode è molto utile perché consente di disegnare il diagramma della fase anche se il diagramma delle ampiezze è soltanto approssimato.
- Se l'ampiezza è costante, la fase è nulla
- Se l'ampiezza cresce, si rileva un anticipo della fase
- Se l'ampiezza decresce, si rileva un ritardo della fase.
La spiegazione della formula
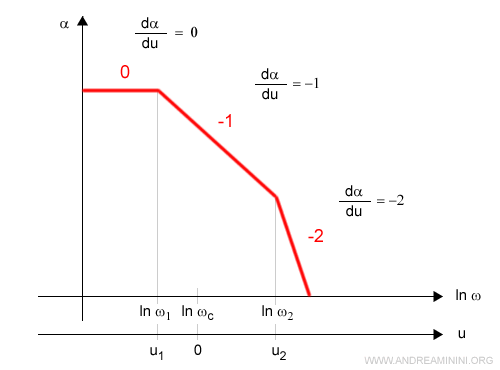
La pendenza del diagramma delle ampiezze è rilevata dalla derivata
$$ \frac{d α}{d u} $$
Dove la variabile u è l'asse delle ascisse ln w con l'origine spostata in corrispondenza di wc.
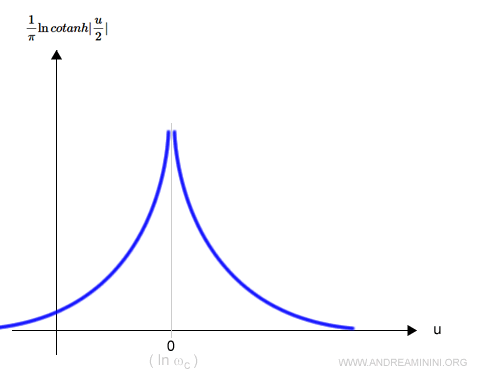
L'altra componente della formula di Bode
$$ \frac{1}{π} \ln cotanh |\frac{u}{2}| $$
Graficamente ha la seguente forma
Unendo i due grafici ottengo.
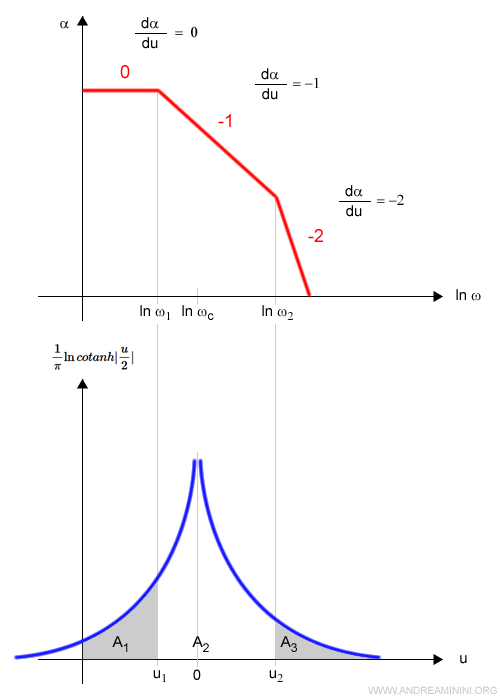
I punti di rottura w1 e w2 corrispondono ai punti u1 e u2 che suddividono l'area al di sotto del grafico in tre aree distinte A1, A2 e A3.
Il prodotto delle aree A1, A2 e A3 per i corrispondenti valori delle pendenze è pari all'area dell'integrale
$$ (0 \cdot A_1 ) + (-1 \cdot A_2 ) + ( -2 \cdot A_3 ) $$
A sua volta l'area dell'integrale è uguale alla fase
$$ β_c = \frac{1}{π} \int_{-∞}^{+∞} \frac{d \: α}{d \: u} \ln cotanh | \frac{u}{2}| du $$
Se il diagramma delle ampiezze è composto da semplici spezzate, il calcolo dell'integrale diventa molto semplice, perché la derivata dα/du è costante a tratti.
E così via.
