La funzione di trasferimento di Bode

In questi appunti spiego come si ottiene la funzione di trasferimento nella rappresentazione di Bode.

Come ottenere la funzione di trasferimento di Bode

Un sistema dinamico con un ingresso X(s) e un'uscita Y(s)

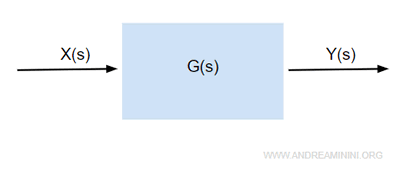
E' caratterizzato da una funzione di trasferimento fratta

$$ G(s) = \frac{Y(s)}{X(s)} = \frac{ \sum_{i=0}^{m} b_i \cdot s^i }{ \sum_{i=0}^{n} a_i \cdot s^i } $$

$$ G(s) = \frac{b_ms^m+...+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+...+a_0} $$

Pa sso alla rappresentazione zeri-poli fattorizzando i polinomi al numeratore e al denominatore, mettendo in evidenza gli zeri (z) e i poli (p).

$$ G(s) = \frac{b_m(s-z_1) \cdot \cdot \cdot (s-z_m)}{a_n \cdot (s-p_1) \cdot \cdot \cdot (s-p_n)} $$

Considerando il guadagno alle alte frequenze K' diventa

$$ G(s) = \frac{b_m}{a_n} \cdot \frac{(s-z_1) \cdot \cdot \cdot (s-z_m)}{ (s-p_1) \cdot \cdot \cdot (s-p_n) } $$

$$ G(s) = K' \cdot \frac{ \prod_{i=1}^m (s-z_i) }{ \prod_{i=1}^n (s-p_i) } $$

Gli zeri e i poli possono essere reali (asse x) o complessi (asse y).

Per ipotesi nella F(s) ci sono R zeri reali e S zeri complessi. Nella X(s) invece ci sono R' poli reali e S' poli complessi.

Posso riscrivere la funzione di trasferimento separando i prodotti degli zeri reali dagli zeri complessi e i prodotti dei poli reali dai poli complessi.

$$ G(s) = K' \cdot \frac{ \prod_{i=1}^R (s-z_i) }{ \prod_{i=1}^{R'} (s-p_i) } \cdot \frac{ \prod_{i=R+1}^{R+S} (s-z_i) }{ \prod_{i=R'+1}^{R'+S'} (s-p_i) } $$

Considerando anche la molteplicità v₀ e v₀' dei poli nell'origine, la funzione di trasformazione diventa

$$ G(s) = K' \cdot \frac{ \prod_{i=v_0+1}^R (s-z_i) }{ \prod_{i=v_0+1}^{R'} (s-p_i) } \cdot \frac{ \prod_{i=R+1}^{R+S} (s-z_i) }{ \prod_{i=R'+1}^{R'+S'} (s-p_i) } $$

Aggiungo al denominatore anche s^v che identifica l'eventuale polo nell'origine di molteplicità v.

Se non ci sono poli nell'origine basta indicare v=0.

$$ G(s) = K' \cdot \frac{ \prod_{i=v_0+1}^R (s-z_i) }{ s^v \cdot \prod_{i=v_0+1}^{R'} (s-p_i) } \cdot \frac{ \prod_{i=R+1}^{R+S} (s-z_i) }{ \prod_{i=R'+1}^{R'+S'} (s-p_i) } $$

Il polo nell'origine. La costante tempo non è definita in caso di polo reale nullo. Si parla in questo caso di polo nell'origine. Questi casi vanno considerati a parte rispetto agli altri poli reali non nulli.

Sostituisco le radici complesse (zeri e poli) con le coordinate cartesiane del numero complesso α+jω

Per ogni radice complessa α+jω esiste la radice coniugata α-jω

$$ G(s) = K' \cdot \frac{ \prod_{i=v_0+1}^R (s-z_i) }{ s^v \cdot \prod_{i=v_0+1}^{R'} (s-p_i) } \cdot \frac{ \prod_{i=R+1}^{R+S} (s-(α_i+jω_i)) \cdot (s-(α_i-jω_i)) }{ \prod_{i=R'+1}^{R'+S'} (s-(α'_i+jω'_i)) \cdot (s-(α'_i-jω'_i)) } $$

A questo punto si può passare alla rappresentazione di Bode.

Un generico binomio (s-p) corrispondente a un polo o zero reale può essere riscritto in modo equivalente

$$ (s-a) = -a(1- \frac{s}{a}) $$

Un generico binomio (s-p) corrispondente a un polo reale p=1 può essere riscritto in modo equivalente

$$ (s-a) = -a(1- \frac{s}{a}) $$

Nel moto aperiodico la costante di tempo è τ=-1/a. Quindi, a=-1/τ.

$$ (s-a) = (- (\frac{-1}{τ}) (1- \frac{s}{(\frac{-1}{τ})}) $$

$$ (s-a) = \frac{1}{τ} \cdot (1+τs) $$

Sostituisco l'espressione 1/τ(1+τs) ai poli e zeri reali (s-a)

$$ G(s) = K' \cdot \frac{ \prod_{i=v_0+1}^R \frac{1}{τ_i} \cdot (1+τ_is) }{ s^v \cdot \prod_{i=v'_0+1}^{R'} \frac{1}{τ'_i} \cdot (1+τ'_is) } \cdot \frac{ \prod_{i=R+1}^{R+S} (s-(α_i+jω_i)) \cdot (s-(α_i-jω_i)) }{ \prod_{i=R'+1}^{R'+S'} (s-(α'_i+jω'_i)) \cdot (s-(α'_i-jω'_i)) } $$

A questo punto modifico anche i poli e gli zeri complessi.

$$ (s-(α+jω)) \cdot (s-(α-jω)) $$

$$ (s-α-jω) \cdot (s-α+jω) $$

$$ s^2-as+sjω-as+a^2-ajω -sjω+ajω-(jω)^2 $$

$$ s^2-2as+a^2-(j)^2(ω)^2 $$

Per la proprietà dei numeri complessi il quadrato dell'unità immaginaria j² è uguale a -1

$$ s^2-2as+a^2-(-1)(ω)^2 $$

$$ s^2-2as+a^2+ω^2 $$

Nota. La radice quadrata della somma a²+w² è la pulsazione naturale $$ w_n = \sqrt{ a^2+w^2 } $$

Sostituisco a²+w² con la pulsazione naturale w_n²

$$ s^2-2as+ω_n^2 $$

Metto in evidenza la pulsazione naturale w_n² e con qualche passaggio algebrico

$$ ω_n^2 \cdot ( 1 - \frac{2as}{ω_n^2} + \frac{s^2}{ω_n^2} ) $$

Nota. Il rapporto -a/w_n è il coefficiente di smorzamento δ che per definizione |δ|∈[0,1]. $$ δ = - \frac{a}{w_n} $$

Sostituisco -a/w_n con il coefficiente di smorzamento δ

$$ ω_n^2 \cdot ( 1 - \frac{2as}{ω_n^2} + \frac{s^2}{ω_n^2} ) $$

$$ ω_n^2 \cdot ( 1 - \frac{a}{ω_n} \cdot \frac{2s}{ω_n} + \frac{s^2}{ω_n^2} ) $$

$$ ω_n^2 \cdot ( 1 + δ \cdot \frac{2s}{ω_n} + \frac{s^2}{ω_n^2} ) $$

$$ ω_n^2 \cdot ( 1 + \frac{2sδ}{ω_n} + \frac{s^2}{ω_n^2} ) $$

Pertanto, i poli e gli zeri complessi sono uguali a

$$ (s-(α+jω)) \cdot (s-(α-jω)) = ω_n^2 \cdot ( 1 + \frac{2sδ}{ω_n} + \frac{s^2}{ω_n^2} ) $$

Sostituisco la precedente nella funzione di trasferimento

$$ G(s) = K' \cdot \frac{ \prod_{i=v_0+1}^R \frac{1}{τ_i} \cdot (1+τ_is) }{ s^v \cdot \prod_{i=v'_0+1}^{R'} \frac{1}{τ'_i} \cdot (1+τ'_is) } \cdot \frac{ \prod_{i=R+1}^{R+S} (s-(α_i+jω_i)) \cdot (s-(α_i-jω_i)) }{ \prod_{i=R'+1}^{R'+S'} (s-(α'_i+jω'_i)) \cdot (s-(α'_i-jω'_i)) } $$

$$ G(s) = K' \cdot \frac{ \prod_{i=v_0+1}^R \frac{1}{τ_i} \cdot (1+τ_is) }{ s^v \cdot \prod_{i=v'_0+1}^{R'} \frac{1}{τ'_i} \cdot (1+τ'_is) } \cdot \frac{ \prod_{i=R+1}^{R+S} ω_n^2 \cdot ( 1 + \frac{2sδ_i}{ω_{n,i}} + \frac{s^2}{ω_{n,i}^2} ) }{ \prod_{i=R'+1}^{R'+S'} ω_{n,i}^{'2} \cdot ( 1 + \frac{2sδ'_i}{ω_{n,i}^{'}} + \frac{s^2}{ω_{n,i}^{'2}} ) } $$

Nota. I parametri τ, ω, δ sono importanti soprattutto al denominatore ( poli ) perché determinano l'evoluzione della funzione. Quindi, hanno un significato fisico. Quelli al numeratore sono invece meno importanti.

dove K' = b/a_n

$$ G(s) = \frac{b_m}{a_n} \cdot \frac{ \prod_{i=v_0+1}^R \frac{1}{τ_i} \cdot (1+τ_is) }{ s^v \cdot \prod_{i=v'_0+1}^{R'} \frac{1}{τ'_i} \cdot (1+τ'_is) } \cdot \frac{ \prod_{i=R+1}^{R+S} ω_n^2 \cdot ( 1 + \frac{2sδ_i}{ω_{n,i}} + \frac{s^2}{ω_{n,i}^2} ) }{ \prod_{i=R'+1}^{R'+S'} ω_{n,i}^{'2} \cdot ( 1 + \frac{2sδ'_i}{ω_{n,i}^{'}} + \frac{s^2}{ω_{n,i}^{'2}} ) } $$

Raggruppo a sinistra alcuni parametri caratteristici

$$ G(s) = [ \frac{b_m}{a_n} \cdot \frac{\prod_{i=v_0+1}^R \frac{1}{τ_i}}{\prod_{i=v'_0+1}^{R'} \frac{1}{τ'_i}} \cdot \frac{ \prod_{i=R+1}^{R+S} ω_n^2 }{ \prod_{i=R'+1}^{R'+S'} ω_{n,i}^{'2} } ] \cdot \frac{ \prod_{i=v_0+1}^R (1+τ_is) }{ s^v \cdot \prod_{i=v'_0+1}^{R'} (1+τ'_is) } \cdot \frac{ \prod_{i=R+1}^{R+S} ( 1 + \frac{2sδ_i}{ω_{n,i}} + \frac{s^2}{ω_{n,i}^2} ) }{ \prod_{i=R'+1}^{R'+S'} ( 1 + \frac{2sδ'_i}{ω_{n,i}^{'}} + \frac{s^2}{ω_{n,i}^{'2}} ) } $$

La prima componente a sinistra è il guadagno di Bode che generalmente è indicato con la costante K.

$$ K = \frac{b_m}{a_n} \cdot \frac{\prod_{i=v_0+1}^R \frac{1}{τ_i}}{\prod_{i=v'_0+1}^{R'} \frac{1}{τ'_i}} \cdot \frac{ \prod_{i=R+1}^{R+S} ω_n^2 }{ \prod_{i=R'+1}^{R'+S'} ω_{n,i}^{'2} } $$

$$ K = \frac{b_m}{a_n} \cdot \frac{ \prod_{i=v'_0+1}^{R'} τ'_i }{ \prod_{i=v_0+1}^R τ_i } \cdot \frac{ \prod_{i=R+1}^{R+S} ω_n^2 }{ \prod_{i=R'+1}^{R'+S'} ω_{n,i}^{'2} } $$

Nota. Il guadagno di Bode K può essere calcolato rapidamente usando i coefficienti diversi da zero più bassi b_k e a_k a numeratore e denominatore della funzione di trasferimento. Dove k=min(j). $$ K=\frac{b_k}{a_k} $$ Quindi, se la funzione di trasferimento non ha poli e zeri all'origine il guadagno è semplicemente $$ K = \frac{b_0}{a_0} $$

Quindi, posso riscrivere la funzione di trasferimento indicando semplicemente K

$$ G(s) = K \cdot \frac{ \prod_{i=v_0+1}^R (1+τ_is) }{ s^v \cdot \prod_{i=v'_0+1}^{R'} (1+τ'_is) } \cdot \frac{ \prod_{i=R+1}^{R+S} ( 1 + \frac{2sδ_i}{ω_{n,i}} + \frac{s^2}{ω_{n,i}^2} ) }{ \prod_{i=R'+1}^{R'+S'} ( 1 + \frac{2sδ'_i}{ω_{n,i}^{'}} + \frac{s^2}{ω_{n,i}^{'2}} ) } $$

Ho ottenuto la funzione di trasferimento nella rappresentazione di Bode.

$$ G(s) = K \cdot \frac{ \ (1+τ_1s) \cdot (1+τ_2s) \cdot \cdot \cdot ( 1 + \frac{2sδ_1}{ω_{n,1}} + \frac{s^2}{ω_{n,1}^2} ) \cdot ( 1 + \frac{2sδ_2}{ω_{n,2}} + \frac{s^2}{ω_{n,2}^2} ) \cdots }{ s^v \cdot (1+τ'_1s) \cdot (1+τ'_2s) \cdot \cdot \cdot ( 1 + \frac{2sδ'_1}{ω_{n,1}^{'}} + \frac{s^2}{ω_{n,1}^{'2}} ) \cdot ( 1 + \frac{2sδ'_2}{ω_{n,2}^{'}} + \frac{s^2}{ω_{n,2}^{'2}} ) \cdots } $$

con il guadagno uguale a

$$ K = K' \cdot \frac{ τ'_1 \cdot τ'_2 \cdots ω_{n,1}^{2} \cdot ω_{n,2}^{2} \cdots }{ τ_1 \cdot τ_2 \cdots ω_{n,1}^{'2} \cdot ω_{n,2}^{'2} \cdots } $$

Questa rappresentazione mi permette di usare i diagrammi di Bode.

Un esempio pratico

Ho la seguente funzione di trasferimento

$$ G(s) = \frac{40s-10}{s^3+21s^2+20s} $$

Per costruire la rappresentazione nella forma di bode analizzo il polinomio caratteristico al denominatore

$$ G(s) = \frac{40s-10}{s(s+1)(s+20)} $$

Con qualche passaggio algebrico metto in evidenza -10 al numeratore e 20 al denominatore, per poterli semplificare

$$ G(s) = \frac{-10 \cdot (1-4s)}{ 20s(s+1)(1+ \frac{s}{20})} $$

$$ G(s) = \frac{-10}{20} \cdot \frac{ 1-4s}{ s(s+1)(1+ \frac{s}{20})} $$

e ottengo la funzione di trasferimento nella forma di Bode

$$ G(s) = \frac{-1}{2} \cdot \frac{ 1-4s}{ s(s+1)(1+ \frac{s}{20})} $$

Dove K=-1/2 è il guadagno di Bode

E così via.