Posizione e orientamento di un braccio robotico

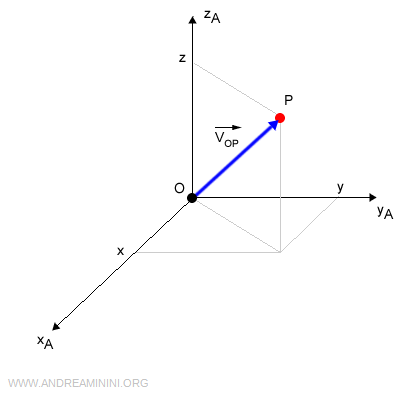
Qualsiasi punto nello spazio P(x,y,z) posso indicarlo tramite le sue coordinate cartesiane rispetto a un sistema di riferimento RF_A (x_A, y_A, z_A)

Dove x_A, y_A, z_A sono i versori del sistema di riferimento RF_A.

$$ RF_A ( \vec{x}_A \ , \ \vec{y}_A \ , \ \vec{z}_A ) $$

Il punto nello spazio P(x,y,z) è raggiunto da un vettore V_OP che congiunge l'origine O del sistema con il punto P.

Posso rappresentare il punto P anche tramite le sue coordinate cilindriche o sferiche.

$$ P(r, θ,h) $$

Dove r è il raggio del cilindro, θ è l'angolo del raggio rispetto all'asse x, h è l'altezza.

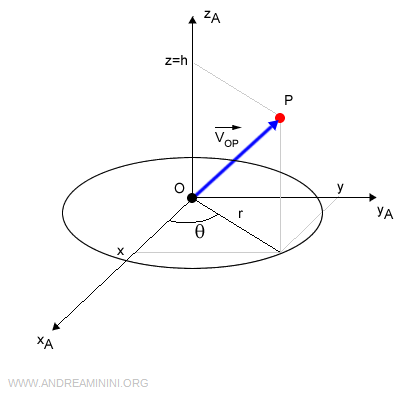
Per passare dalle coordinate cilindriche a quelle cartesiane basta ricordarsi che le componenti del vettore sono i coseni direttori

$$ x= r \cdot \cos θ $$

$$ y= r \cdot \sin θ $$

$$ z= h $$

Allo stesso modo posso ottenere le coordinate cilindriche a partire dalle coordinate cartesiane.

$$ r = \sqrt{x^2+y^2} $$

$$ θ = \arctan( \frac{y}{x} ) $$

$$ h = z $$

Nota. Il raggio r si misura usando il teorema di Pitagora poiché conosco la lunghezza dei cateti x e y. L'angolo θ è il rapporto y/x. $$ \frac{y}{x} = \frac{\sin θ}{ \cos θ} $$ Sapendo dalla trigonometria che il rapporto tra sin(θ)/cos(θ)=tan(θ) è uguale alla tangente. $$ \frac{y}{x} = \tan θ $$ Per trovare l'angolo θ applico la funzione inversa della tangente (l'arcotangente) a entrambi i membri dell'equazione. $$ \arctan \frac{y}{x} = \arctan( \tan θ) $$ $$ \arctan \frac{y}{x} = θ $$ Devo però ricordarmi che l'arcotangente funziona solo nell'intervallo (-π/2, π/2) ossia per 180°. Pertanto, per farla funzionare su 360° devo usare la formula θ=arctan(y/x) nell'intervallo (-π/2, π/2) e la formula θ=180°+arctan(y/x) nell'intervallo (π/2, 2/3π). In alternativa, posso usare la funzione atan2(y,x) che adegua automaticamente il calcolo e funziona su tutti i quadranti. Il che è decisamente più comodo. $$ θ = atan2(y,x)$$ Infine l'altezza h è banalmente coincidente con z. Quindi c'è poco da aggiungere. $$ h=z $$

Una volta decisa la posizione, devo inicare l'orientamento del braccio.

Per farlo utilizzo il punto P come l'origine O' di un secondo sistema di riferimento RF_B

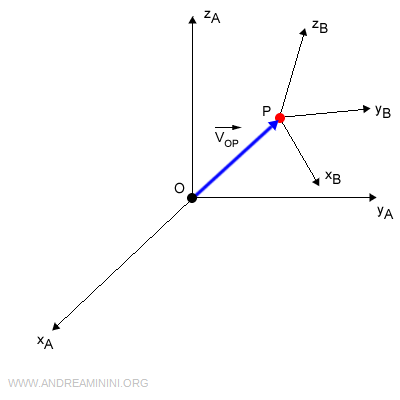
Questo secondo sistema di riferimento RF_B è caratterizzato da altri tre versori x_B,y_B,z_B

$$ R_B = [ \vec{x}_B \ , \ \vec{y}_B \ , \ \vec{z}_B ] $$

Per indicare i tre versori con il sistema di riferimento A uso la notazione ^AX_B, ^Ay_B, ^Az_B

$$ ^AR_B = [ ^A\vec{x}_B \ , \ ^A\vec{y}_B \ , \ ^A\vec{z}_B ] $$

Scendendo più in dettaglio, i versori del sistema di riferimento RF_B indicati rispetto al sistema di riferimento RF_A sono i seguenti:

$$ ^A \vec{x_B} = \ ^Ax_B \cdot \vec{x} + \ ^A x_y \cdot \vec{y} + \ ^A x_z \cdot \vec{z} $$

$$ ^A \vec{y_B} = \ ^Ay_B \cdot \vec{x} \ + \ ^Ay_y \cdot \vec{y} + \ ^A y_z \cdot \vec{z} $$

$$ ^A \vec{z_B} = \ ^Az_B \cdot \vec{x} \ + \ ^Az_y \cdot \vec{y} \ + \ ^A z_z \cdot \vec{z} $$

Un esempio pratico

Il riferimento di partenza ha una base composta dai versori

$$ x = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} $$

$$ y = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$

$$ z = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$

Si tratta di una base canonica

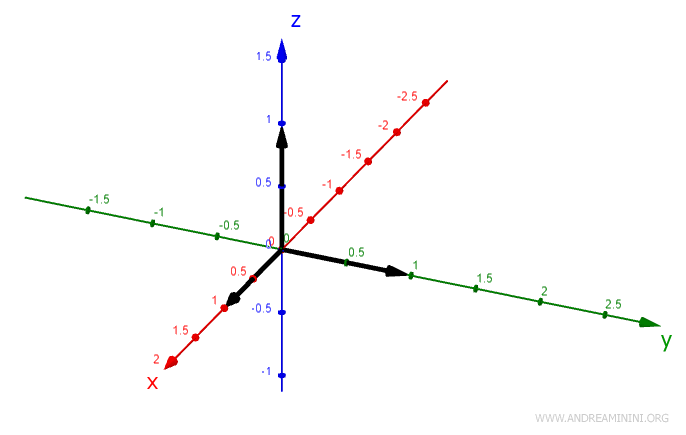
Il primo braccio è un vettore che congiunge l'origine O(0;0;0) e il punto P(0;1;1).

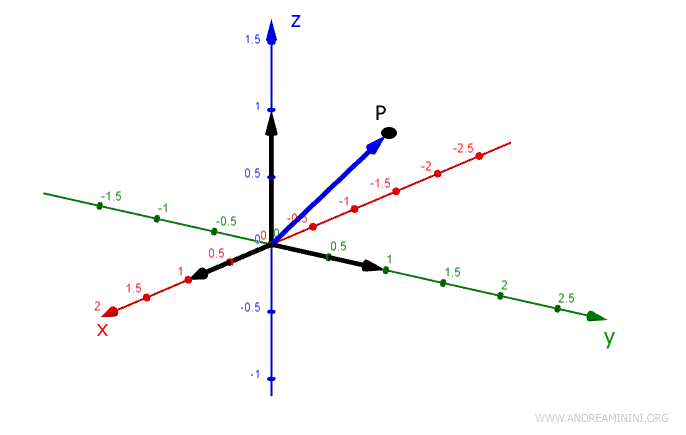
Il punto P è l'origine il secondo riferimento RF_B che si presenta con un diverso orientamento rispetto al primo.

L'asse z del sistema RF_B è ruotato di 90° rispetto al primo.

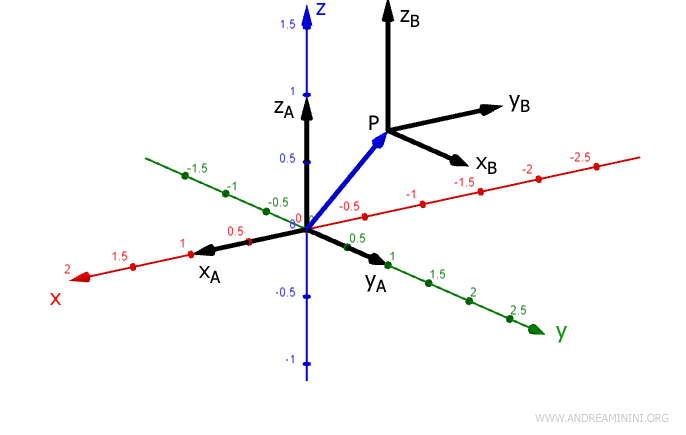
Il secondo braccio congiuge l'origine O_B=P con il punto P_B che si trova alle coordinate ^BP_B(0;1;1) del sistema di riferimento RF_B

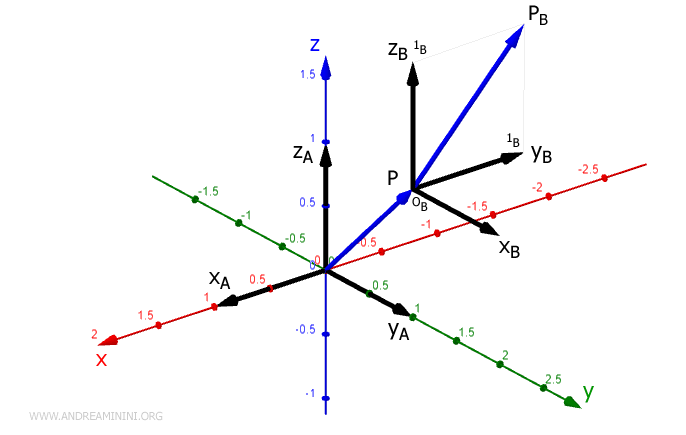
Nel sistema di riferimento RF_A il punto ^BP_B(0;1;1) si trova alle coordinate ^AP_B(-1;1;2).

Per trovare le coordinate del punto P_B nel riferimento RF_A devo calcolare la matrice di trasformazione tra i due sistemi di riferimento.

La matrice dei versori del riferimento A è composta dai suoi tre versori disposti in colonna

$$ M_A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Per calcolare i versori del riferimento B usando le coordinate del riferimento A uso la matrice di rotazione con una rotazione di φ=90° sull'asse z ( Φ=0 e ψ=0 sugli altri assi ).

$$ R = R_x(\psi) \cdot R_y(\theta) \cdot R_z(\phi) $$

Dove

$$ R_x = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos(\psi) & -\sin(\psi) \\ 0 & \sin(\psi) & \cos(\psi) \end{pmatrix} $$

$$ R_y = \begin{pmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{pmatrix} $$

$$ R_z = \begin{pmatrix} \cos(\phi) & -sin(\phi) & 0 \\ \sin(\phi) & \cos(\phi) & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Quindi la matrice di rotazione è

$$ R = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos(\psi) & -\sin(\psi) \\ 0 & \sin(\psi) & \cos(\psi) \end{pmatrix} \cdot \begin{pmatrix} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{pmatrix} \cdot \begin{pmatrix} \cos(\phi) & -sin(\phi) & 0 \\ \sin(\phi) & \cos(\phi) & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Sapendo che φ=90° , Φ=0 e ψ=0

$$ R = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos(0) & -\sin(0) \\ 0 & \sin(0) & \cos(0) \end{pmatrix} \cdot \begin{pmatrix} \cos(0) & 0 & \sin(0) \\ 0 & 1 & 0 \\ -\sin(0) & 0 & \cos(0) \end{pmatrix} \cdot \begin{pmatrix} \cos(90°) & -sin(90°) & 0 \\ \sin(90°) & \cos(90°) & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

$$ R = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

$$ R = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Le colonne della matrice R sono i versori del riferimento ^ARF_B a cui devo aggiungere l'origine ^AO_B

$$ ^Ax_B = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + ^AO_B $$

$$ ^Ay_B = \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} + ^AO_B $$

$$ ^Az_B = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + ^AO_B $$

Nota. Quindi la matrice dei versori del riferimento B è $$ M_B = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

Sapendo che le coordinate che l'origine ^AO_B=P=(0;1;1).

$$ ^Ax_B = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

$$ ^Ay_B = \begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

$$ ^Az_B = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

Pertanto le coordinate dei versori del ^ARF_B nel riferimento A sono le seguenti

$$ ^Ax_B = \begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix} $$

$$ ^Ay_B = \begin{pmatrix} -1 \\ 1 \\ 1 \end{pmatrix}$$

$$ ^Az_B = \begin{pmatrix} 0 \\ 1 \\ 2 \end{pmatrix} $$

In questo modo ottengo le coordinate dei versori del riferimento B nel riferimento A.

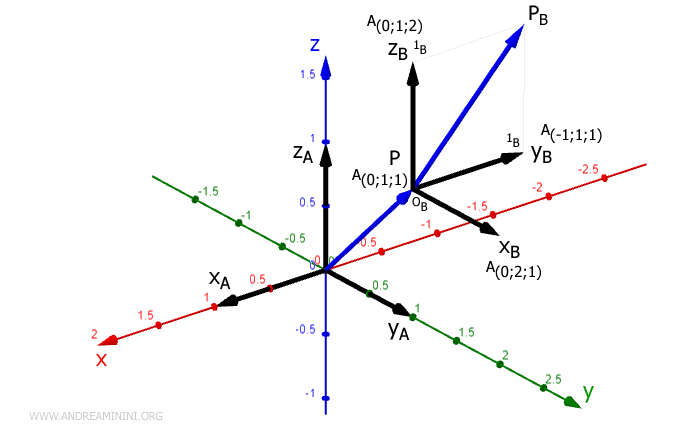
Le coordinate del punto ^BP_B nel riferimento B sono

$$ ^BP_B = \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

Traformo le coordinate del punto ^AP_B nel riferimento A tramite la matrice di trasformazione M_A^-1M_B del cambio di base

$$ ^AP_B = M_A^{-1} \cdot M_B \cdot \ ^BP_B + ^AO_B $$

$$ ^AP_B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}^{-1} \cdot \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

$$ ^AP_B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

$$ ^AP_B = \begin{pmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

$$ ^AP_B = \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} $$

$$ ^AP_B = \begin{pmatrix} -1 \\ 1 \\ 2 \end{pmatrix} $$

Dal punto di vista grafico

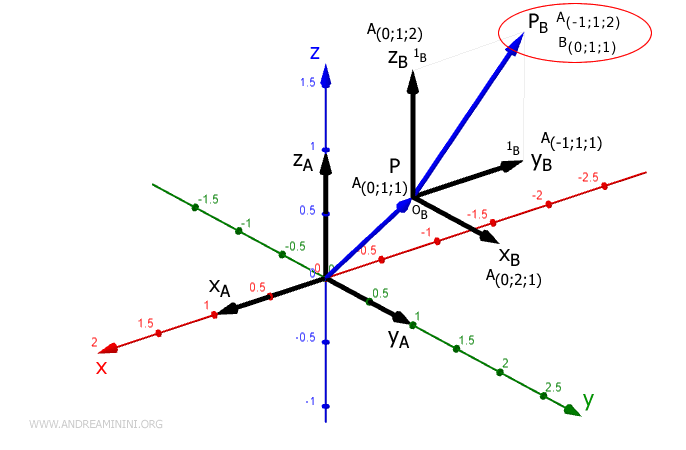
A sua volta il punto ^AP_B può essere l'origine di un terzo braccio.

E così via.