L'equazione vettoriale e parametrica della retta

Come calcolare l'equazione vettoriale e parametrica di una retta

Posso rappresentare un punto qualsiasi P di una retta nello spazio o nel piano tramite la seguente forma vettoriale:

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t \cdot v_r $$

Dove

• P₀ è un punto qualsiasi appartenente alla retta
• t è il parametro che individua tutti i punti della retta
• vr è il vettore direttore della retta

Essendo OP e OP₀ due vettori individuati da due punti dello spazio o del piano, posso rappresentarli anche in questo modo.

$$ \overrightarrow{OP} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$

$$ \overrightarrow{OP_0} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Quindi, posso riscrivere l'equazione vettoriale in questo modo

$$ \overrightarrow{OP} = \overrightarrow{OP_0} + t \cdot v_r $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot v_r $$

Infine, il vettore direttore è il vettore che determina la direzione della retta.

$$ v_r = \begin{pmatrix} l \\ m \\ n \end{pmatrix} $$

Come trovare il vettore direttore? In due punti P₁ e P₂ passa una e una sola retta. E' quindi sufficiente calcolare il vettore P₁P₂ che passa in due punti qualsiasi della retta. $$ v_r = \overrightarrow{P_1P_2} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} $$

Pertanto, l'equazione vettoriale della retta nello spazio è la seguente.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} $$

Una volta trovata l'equazione vettoriale, è molto facile ottenere l'equazione parametrica della retta.

Devo solo riscrivere l'equazione vettoriale come un sistema di equazioni.

$$ \begin{cases} x = x_0 + t \cdot l \\ y = y_0 + t \cdot m \\ z = z_0 + t \cdot n \end{cases} $$

Per ogni retta del piano o dello spazio esistono infinite equazioni vettoriali o parametriche perché esistono infiniti vettori direttori multipli e infiniti punti P₀ della retta tra cui scegliere.

Esempio

Devo trovare l'equazione vettoriale di una retta che passa in due punti dello spazio R³:

$$ P_1 = \begin{pmatrix} 2 \\ 3 \\ 5 \end{pmatrix} $$

$$ P_2 = \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} $$

Grazie alle coordinate dei due punti posso facilmente calcolare il vettore direttore della retta.

$$ v_r = \overrightarrow{P_1P_2} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} = \begin{pmatrix} 1 - 2 \\ 0 - 3 \\ -3 - 5 \end{pmatrix} $$

$$ v_r = \overrightarrow{P_1P_2} = \begin{pmatrix} -1 \\ - 3 \\ -8 \end{pmatrix} $$

Posso così cominciare a scrivere l'equazione vettoriale della retta.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ - 3 \\ -8 \end{pmatrix} $$

Ora mi serve un punto qualsiasi P₀ della retta

Ne conosco già due ( P₁ e P₂ ). Quindi, mi basta scegliere uno dei due. Scelgo P₁.

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \\ 5 \end{pmatrix} + t \cdot \begin{pmatrix} -1 \\ - 3 \\ -8 \end{pmatrix} $$

Ho così ottenuto l'equazione vettoriale della retta nella forma completa.

A questo punto la trasformo in un sistema di equazioni per trovare l'equazione parametrica della retta.

$$ \begin{cases} x = 2 - t \\ y = 3 - 3t \\ z = 5 -8t \end{cases} $$

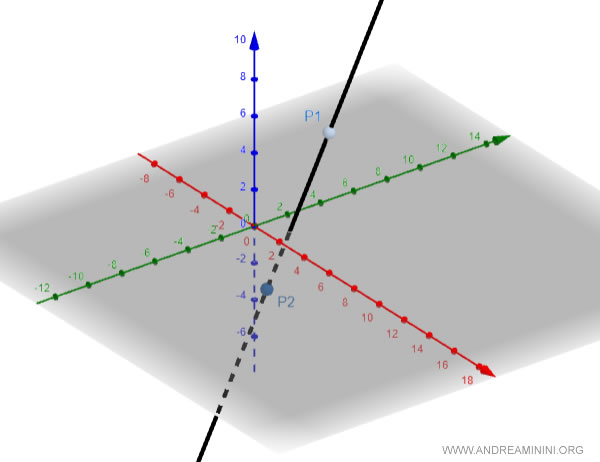
Ecco la rappresentazione grafica della retta su un diagramma cartesiano a tre dimensioni

Come calcolare l'equazione cartesiana della retta dalla parametrica?

Scelgo una variabile x,y,z per ottenere il parametro t.

Ad esempio, scelgo la x

$$ \begin{cases} t = 2-x \\ y = 3 - 3t \\ z = 5 -8t \end{cases} $$

Poi sostituisco il parametro t nelle altre due equazioni.

$$ \begin{cases} y = 3 - 3(2-x) \\ z = 5 -8(2-x) \end{cases} $$

$$ \begin{cases} y = 3 -6 +3x \\ z = 5 - 16+8x \end{cases} $$

$$ \begin{cases} y = -3 +3x \\ z = -11+8x \end{cases} $$

Ho così ottenuto l'equazione cartesiana della retta nella spazio.

E' un sistema composto da due equazioni.

$$ \begin{cases} -y -3 +3x = 0 \\ -z -11+8x = 0 \end{cases} $$

E così via