I coseni direttori della retta nello spazio
I coseni direttori misurano gli angoli di una retta orientata rispetto agli assi cartesiani x,y,z.
Il concetto è identico ai coseni direttori della retta sul piano.
Nello spazio, però, le coordinate da considerare sono tre.
Come calcolare i coseni direttori
In primo luogo bisogna considerare una retta orientata nello spazio.
Cos'è una retta orientata? E' una retta a cui è assegnato un vettore direttore ossia un verso. Ogni retta ha due possibili vettori direttori (versi).
Poi si trasforma il vettore direttore in un versore, dividendolo per la sua norma.
$$ u = \frac{v}{||v||} $$
Le coordinate (x,y,z) del versore sono i coseni direttori della retta.
Ogni coseno direttore misura l'angolo tra il versore della retta (u) e il vettore unitario dell'asse (i,j,k).
$$ cos(\widehat{xr}) = cos(i,u) = \frac{<i,u>}{||i||\cdot||u||} $$
$$ cos(\widehat{yr}) = cos(j,u) = \frac{<j,u>}{||j||\cdot||u||} $$
$$ cos(\widehat{zr}) = cos(k,u) = \frac{<k,u>}{||k||\cdot||u||} $$
Nota. Ogni vettore ha lunghezza unitaria e ha un valore compreso tra +1 e -1. Pertanto, il quadrato della somma dei coseni direttori è sempre uguale a 1. Questa regola è detta relazione fondamentale dei coseni direttori. $$ cos^2(xr) + cos^2(yr) + cos^2(zr) = 1 $$
Un esempio pratico
Ho una retta nello spazio
$$ \begin{cases} x+2y-3=0 \\ y+z-3=0 \end{cases} $$
Ecco la rappresentazione grafica della retta
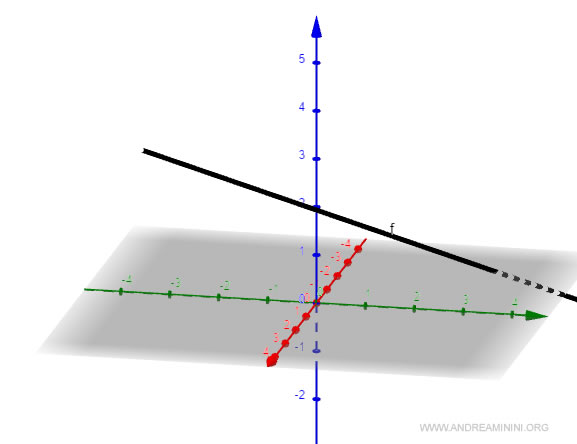
Per conoscere il vettore direttore della retta, trasformo le equazioni cartesiane in parametriche.
$$ \begin{cases} x+2y-3=0 \\ y+z-3=0 \end{cases} $$
Assegno alla z il parametro t e calcolo le altre variabili per sostituzione.
$$ \begin{cases} x+2y-3=0 \\ y+t-3=0 \\ z=t \end{cases} $$
$$ \begin{cases} x+2(3-t)-3=0 \\ y = 3-t \\ z=t \end{cases} $$
$$ \begin{cases} x=-3+2t=0 \\ y = 3-t \\ z=t \end{cases} $$
Riscrivendola in forma vettoriale il vettore direttore è subito evidente:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} -3 \\ 3 \\ 0 \end{pmatrix} + t \cdot \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$
Il vettore direttore della retta è
$$ v = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$
Ecco il vettore direttore sul diagramma cartesiano.
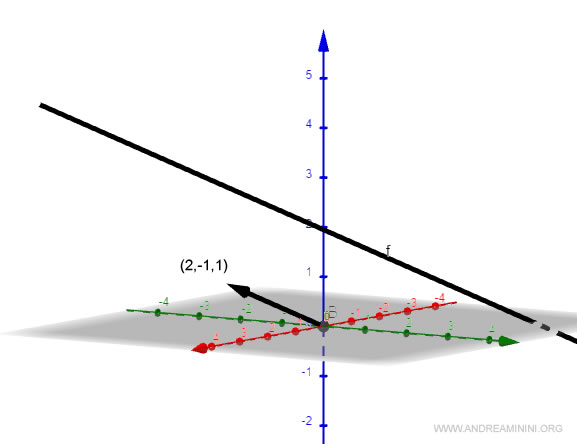
Ovviamente non è detto che la retta abbia il verso del vettore direttore.
Può avere il verso del vettore direttore appena trovato (v) oppure il verso opposto (-v).
$$ -v = \begin{pmatrix} -2 \\ 1 \\ -1 \end{pmatrix} $$
La scelta dipende dall'orientazione della retta nel problema.
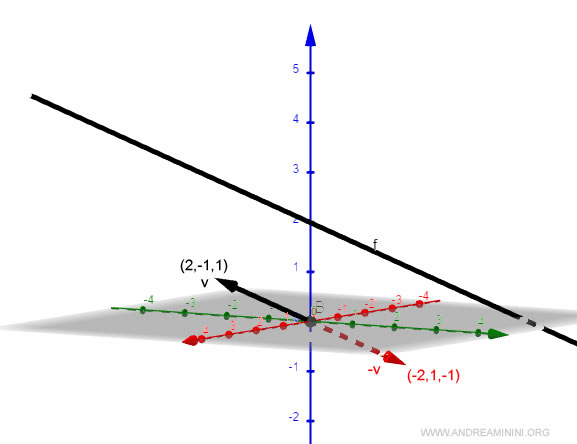
Per ipotesi fisso l'orientazione della retta per le x,z crescenti e y decrescente.
Quindi, il vettore concorde con l'orientazione della retta è
$$ v = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$
A questo punto posso cominciare a calcolare i coseni direttori.
Per prima cosa trasformo il vettore direttore in un versore.
$$ u = \frac{v}{||v||} $$
$$ u = \frac{ \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}}{\sqrt{2^2+(-1)^2+1^2}} $$
$$ u = \frac{ \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}}{\sqrt{6}} $$
$$ u = \begin{pmatrix} \frac{2}{\sqrt{6}} \\ \frac{-1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{pmatrix} $$
Il versore ha la stessa direzione, verso e inclinazione del vettore direttore ma lunghezza unitaria.
Ha il grande vantaggio d'essere utilizzabile nel calcolo trigonometrico.
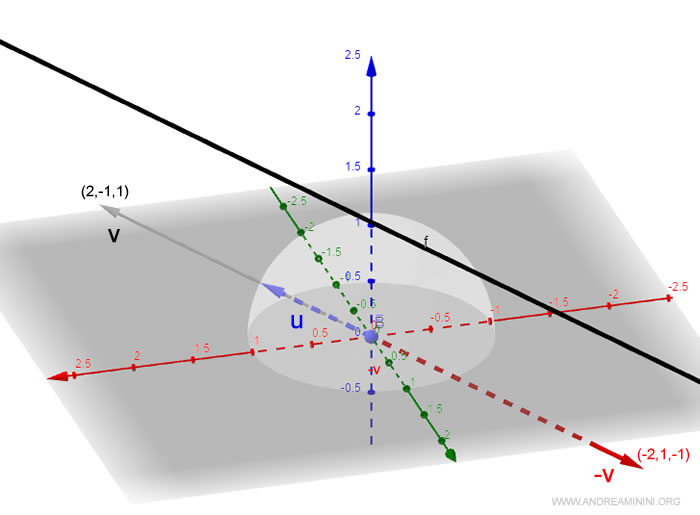
Una volta ottenuto il versore direttore, posso calcolare i coseni direttori.
I vettori degli assi cartesiani sono quelli della base canonica.
$$ i = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} $$
$$ j = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} $$
$$ k = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$
Quindi il coseno direttore dell'angolo rx è
$$ cos(\widehat{xr}) = cos(i,u) = \frac{<i,u>}{||i||\cdot||u||} $$
$$ \cos(\widehat{xr}) = \frac{< \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \begin{pmatrix} \frac{2}{\sqrt{6}} \\ \frac{-1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{pmatrix} > }{1 \cdot \sqrt{(\frac{2}{\sqrt{6}})^2+(\frac{-1}{\sqrt{6}})^2+(\frac{1}{\sqrt{6}})^2} } $$
$$ \cos(\widehat{xr}) = \frac{ \frac{2}{\sqrt{6}} }{ \sqrt{\frac{2}{3}+\frac{1}{6}+\frac{1}{6}} } $$
$$ \cos(\widehat{xr}) = \frac{ \frac{2}{\sqrt{6}} }{ 1 } = 0,82 $$
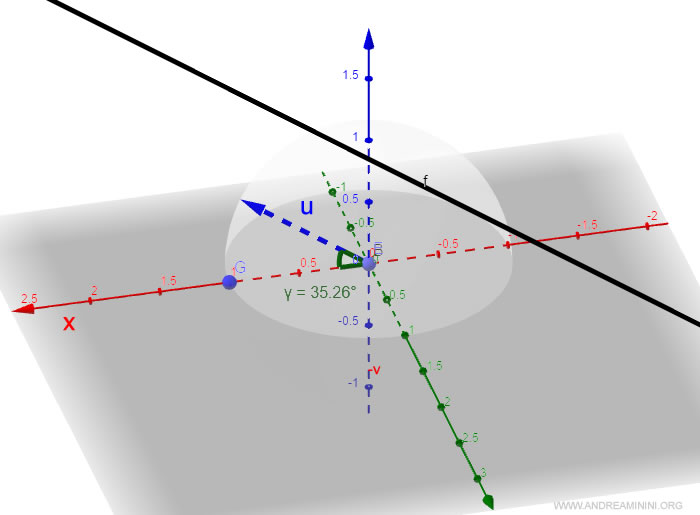
Ho trovato il coseno direttore dell'angolo xr.
Per trovare l'ampiezza dell'angolo xr uso la funzione inversa del coseno ossia l'arcocoseno.
$$ arcos(0,82) = 0,60 π $$
L'angolo xr è uguale a 0,60 radianti, circa 35°.
L'angolo supplementare è ovviamente 180-35 = 145°.
Allo stesso modo posso calcolare il coseno direttore dell'asse y.
$$ cos(\widehat{yr}) = cos(i,u) = \frac{<j,u>}{||i||\cdot||u||} $$
$$ \cos(\widehat{yr}) = \frac{< \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \begin{pmatrix} \frac{2}{\sqrt{6}} \\ \frac{-1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{pmatrix} > }{1 \cdot \sqrt{(\frac{2}{\sqrt{6}})^2+(\frac{-1}{\sqrt{6}})^2+(\frac{1}{\sqrt{6}})^2} } $$
$$ \cos(\widehat{yr}) = \frac{ \frac{-1}{\sqrt{6}} }{ \sqrt{\frac{2}{3}+\frac{1}{6}+\frac{1}{6}} } $$
$$ \cos(\widehat{yr}) = \frac{ \frac{-1}{\sqrt{6}} }{ 1 } = -0,40 $$
Per trovare l'ampiezza dell'angolo xy utilizzo la funzione trigonometrica dell'arcocoseno.
$$ arcos(0,40) = 1,99 π $$
L'angolo yr è uguale a 1,99 radianti, circa 114°.
L'angolo supplementare è ovviamente 180-114 = 66°.

Infine, calcolo il coseno direttore della retta rispetto all'asse z.
$$ cos(\widehat{zr}) = cos(k,u) = \frac{<j,u>}{||i||\cdot||u||} $$
$$ \cos(\widehat{zr}) = \frac{< \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}, \begin{pmatrix} \frac{2}{\sqrt{6}} \\ \frac{-1}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{pmatrix} > }{1 \cdot \sqrt{(\frac{2}{\sqrt{6}})^2+(\frac{-1}{\sqrt{6}})^2+(\frac{1}{\sqrt{6}})^2} } $$
$$ \cos(\widehat{zr}) = \frac{ \frac{1}{\sqrt{6}} }{ \sqrt{\frac{2}{3}+\frac{1}{6}+\frac{1}{6}} } $$
$$ \cos(\widehat{zr}) = \frac{ \frac{1}{\sqrt{6}} }{ 1 } = 0.40 $$
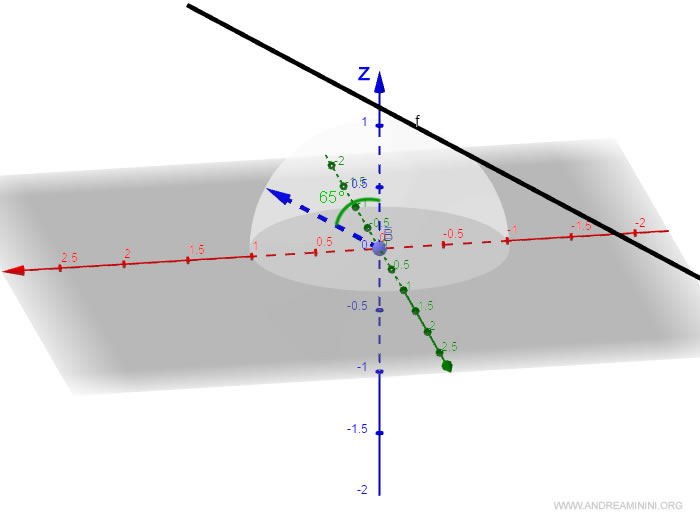
Poi trovo l'ampiezza dell'angolo xz con l'arcoseno.
$$ arcos(0,40) = 1,15 π $$
L'angolo yr è uguale a 1,15 radianti, circa 65°.
L'angolo supplementare è ovviamente 180-65 = 115°.
E così via.
