Come passare da equazione cartesiana a parametrica di una retta

L'equazione cartesiana di una retta del piano è scritta in forma espressa

$$ ax + by + c = 0 $$

L'equazione cartesiana precedente è equivalente all'equazione vettoriale della retta.

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

Dove l'ultimo componente è il vettore direttore v_d della retta.

$$ v_d = \begin{pmatrix} l \\ m \end{pmatrix} $$

Non conosco ancora il vettore direttore.

Al momento conosco soltanto il vettore normale v_n della retta, quello composto dai coefficienti delle incognite.

$$ v_n = \begin{pmatrix} a \\ b \end{pmatrix} $$

Partendo dal presupposto che il vettore normale deve essere un vettore ortogonale al vettore direttore della retta, posso scrivere il prodotto scalare dei vettori uguale a zero.

E' la condizione necessaria per cui due vettori siano ortogonali.

$$ < v_n , v_d > = 0 $$

$$ < \begin{pmatrix} a \\ b \end{pmatrix} , \begin{pmatrix} l \\ m \end{pmatrix} > = 0 $$

$$ a \cdot l + b \cdot m = 0 $$

Posso così calcolare il valore degli elementi l e m del vettore direttore a partire dai coefficienti dell'equazione cartesiana.

$$ a \cdot l = - b \cdot m $$

$$ \frac{l}{m} = \frac{-b}{a} $$

Quindi

$$ \begin{cases} l=-b \\ m=a \end{cases} $$

Pertanto, l'equazione vettoriale della retta è la seguente:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} -b \\ a \end{pmatrix} $$

A questo punto, posso trasformare l'equazione vettoriale in un sistema di equazioni parametriche.

$$ \begin{cases} x = x_0 + α (-b) \\ y = y_0 +α (a) \end{cases} $$

Esistono infinite equazioni parametriche perché esistono infiniti multipli del vettore direttore.

Un esempio pratico

Ho la seguente equazione cartesiana

$$ 2x+3y-4=0 $$

Per maggiore chiarezza la rappresento sul diagramma cartesiano.

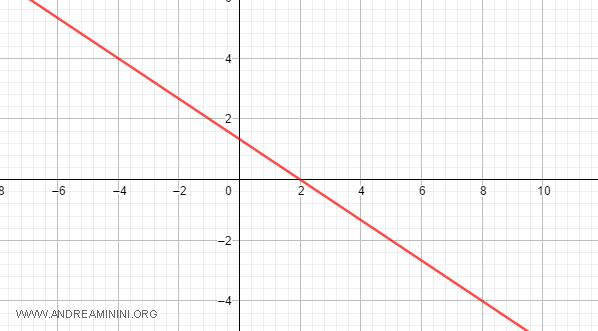
Il vettore normale dei coefficienti della retta è

$$ v_n = \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

Rappresento sul grafico anche il vettore normale.

E' un vettore geometrico che parte dall'origine O e raggiunge le coordinate (x,y)=(2,3).

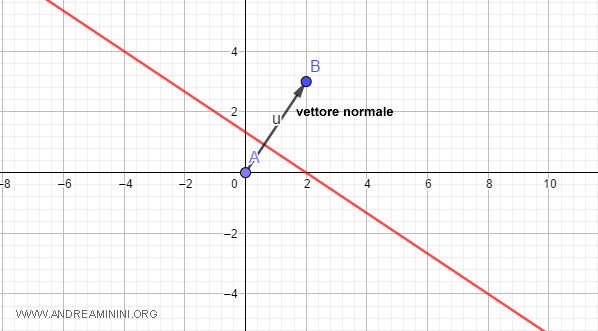
Da questo posso calcolare il vettore direttore dell'equazione vettoriale

$$ v_d = \begin{pmatrix} l \\ m \end{pmatrix} = \begin{pmatrix} -b \\ a \end{pmatrix} = \begin{pmatrix} -3 \\ 2 \end{pmatrix} $$

Rappresento sul diagramma anche il vettore direttore.

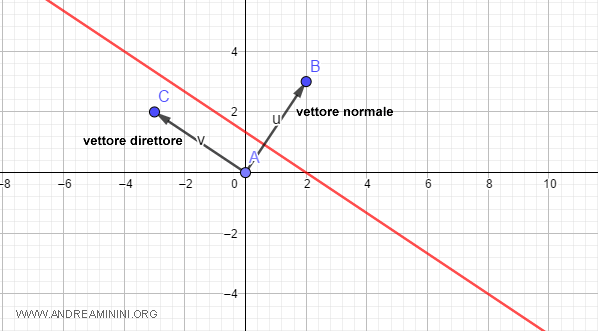
So già che il vettore normale e il vettore direttore sono tra loro vettori ortogonali ossia formano un angolo retto di 90°.

Quindi il loro prodotto scalare è nullo.

$$ < v_n , v_d > = < \begin{pmatrix} 2 \\ 3 \end{pmatrix} , \begin{pmatrix} -3 \\ 2 \end{pmatrix} > = 2 \cdot (-3) + 3 \cdot 2 = -6 +6 = 0 $$

L'equazione vettoriale della retta è la seguente

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$

Ora conosco il vettore direttore vr e posso sostituirlo nell'equazione vettoriale

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + α \cdot \begin{pmatrix} -3 \\ 2 \end{pmatrix} $$

A questo punto trasformo l'equazione vettoriale in un sistema di equazioni.

$$ \begin{cases} x = x_0 -3α \\ y = y_0+2α \end{cases} $$

Dove x₀ e y₀ indica l'intercetta della retta degli assi cartesiani.

$$ x_0 = 0 $$

$$ y_0 = \frac{4 - 2x_0}{3} = \frac{4}{3} $$

Nota. La retta dell'equazione è $$ 2x+3y-4=0 $$ dopo semplici passaggi algebrici diventa $$ 3y=4-2x $$ $$ y=\frac{4-2x}{3} $$ Essendo la x=x₀=0 diventa $$ y=\frac{4}{3} $$

Sostituisco i valori nelle equazioni parametriche e ottengo le equazioni parametriche.

$$ \begin{cases} x = -3α \\ y = \frac{4}{3} + 2α \end{cases} $$

Scorrendo il parametro α ottengo così tutti i punti della retta.

α	x	y
-2	6	-2.66
-1	3	-0.66
0	0	1.33
1	-3	3.33
2	-6	5.33

I punti appartengono tutti alla retta

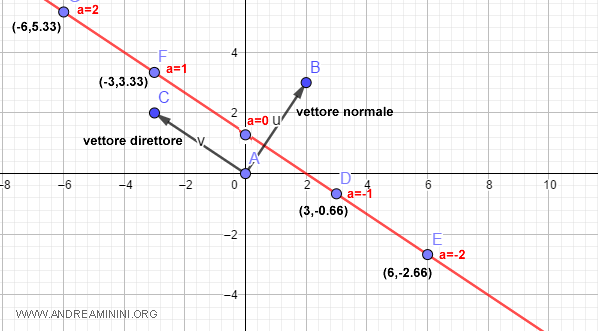
E così via.