Gruppo diedrale

Cosa sono i gruppi diedrali?

Un gruppo diedrale è un gruppo formato dalle isometrie dei poligoni regolari a n lati. E' indicato con la notazione Dn.

Cos'è una isometria?

Un'isometria è un movimento rigido di una figura che non modifica le distanze tra i punti del poligono.

I principali movimenti rigidi sul piano sono:

• la rotazione di un vertice in senso antiorario
  
• la riflessione rispetto a un asse di simmetria

Un esempio pratico

Il triangolo equilatero ha tre vertici (1,2,3) e tre assi di simmetria (a,b,c).

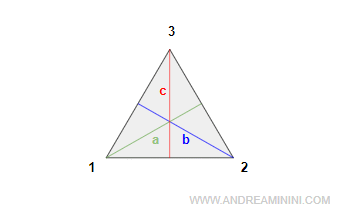
Posso ruotarlo rispetto ai vertici con 3 rotazioni r₁,r₂ e r_i.

L'ultima rotazione è detta rotazione identica (r_i o id) perché è uguale alla figura iniziale.

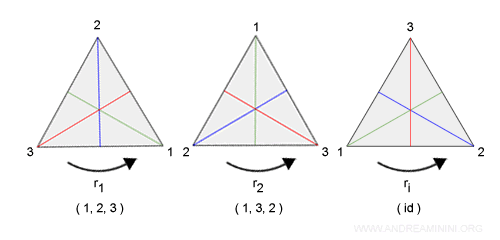
Attenzione. La rotazione deve essere effettuata in senso antiorario se non diversamente specificato. Posso scrivere le rotazioni anche come permutazione di vertici r₁=(1,2,3), r₂=(1,3,2) e r₃=id. Ad esempio, (1,3,2) significa che il vertice 1 prende il posto del vertice 3, il vertice 3 del vertice 2 e, infine, il vertice 2 prende il posto del vertice 1 rispetto alla figura iniziale.

Posso ribaltare ( riflettere ) il triangolo rispetto ai tre assi a,b,c.

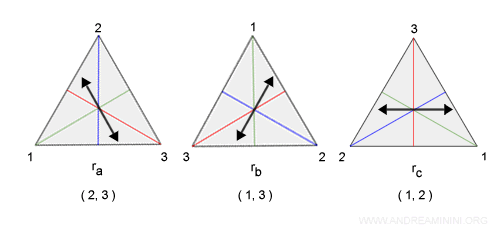
Nota. Anche in questo caso posso rappresentare i movimenti rigidi come permutazione dei vertici rispetto alla figura iniziale. Quindi, r_a = (2,3), r_b=(1,3) e r_c=(1,2). Ad esempio, nella riflessione r_a = (2,3) il vertice 2 prende il posto del vertice 3 e il vertice 3 prende il posto del vertice 2 rispetto alla figura iniziale. Il vertice 1 resta al suo posto, per questa ragione non è indicato nella permutazione.

A questo punto posso anche combinare due movimenti rigidi in sequenza.

Ad esempio, la rotazione r₁ (1,2,3) seguita dalla riflessione r_a (1,2) genera lo stesso risultato della riflessione r_b (1,3).

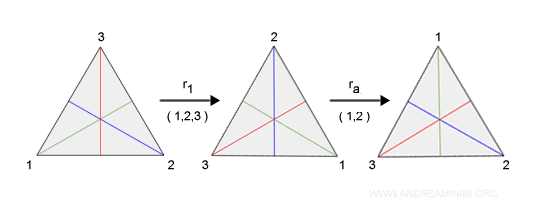
Quindi posso anche scrivere

$$ r_1 \cdot r_a = r_b $$

Allo stesso modo posso calcolare tutti gli altri prodotti.

La seguente tavola della moltiplicazione mostra tutte le possibili combinazioni.

	id	r1	r2	ra	rb	rc
id	id	r1	r2	ra	rb	rc
r1	r1	r2	id	rc	ra	rb
r2	r2	id	r1	rb	rc	ra
ra	ra	rb	rc	id	r1	r2
rb	rb	rc	ra	r2	id	r1
rc	rc	ra	rb	r1	r2	id

Se riscrivo la tavola con le corrispondenti permutazioni di vertici, si nota subito un'importante equivalenza.

	id	(1,2,3)	(1,3,2)	(2,3)	(1,3)	(1,2)
id	id	(1,2,3)	(1,3,2)	(2,3)	(1,3)	(1,2)
(1,2,3)	(1,2,3)	(1,3,2)	id	(1,2)	(2,3)	(1,3)
(1,3,2)	(1,3,2)	id	(1,2,3)	(1,3)	(1,2)	(2,3)
(2,3)	(2,3)	(1,3)	(1,2)	id	(1,2,3)	(1,3,2)
(1,3)	(1,3)	(1,2)	(2,3)	(1,3,2)	id	(1,2,3)
(1,2)	(1,2)	(2,3)	(1,3)	(1,2,3)	(1,3,2)	id

E' la stessa tavola di moltiplicazione del gruppo simmetrico S₃.

Il gruppo diedrale Dn

Un generico gruppo diedrale Dn è formato da n rotazioni sugli n vertici del poligono e n riflessioni sugli n assi di simmetria. $$ n+n = 2n $$

Pertanto, un gruppo diedrale è composto n+n ossia 2n permutazioni dei vertici.

Nota. Ogni rotazione ruota la figura per un angolo pari a $$ \frac{2π}{n} $$

Esempio

Il triangolo è composto da 3+3=6 permutazioni semplici tra rotazioni e riflessioni.

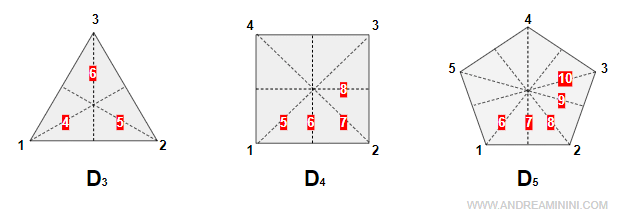
Il quadrato, invece, ha 4+4=8 permutazioni semplici dei vertici.

Il pentagono ha 5 rotazioni e 5 riflessioni ossia 10 permutazioni dei vertici.

E così via.

Soltanto il gruppo diedrale D₃ coincide con il gruppo di permutazioni S₃. Gli altri gruppi diedrali D_n sono solo sottoinsiemi del rispettivo gruppo di permutazioni S_n.

Dimostrazione

Un generico gruppo diedrale D_n è composto da 2n permutazioni.

Il gruppo di permutazioni S_n è invece composto da n! permutazioni. E' quindi più grande.

Ad esempio.

Triangolo

$$ | D_3 | = 6 $$

$$ | S_3| = 3 \cdot 2 \cdot 1 = 6 $$

Quadrato

$$ | D_4 | = 8 $$

$$ | S_4 | = 4 \cdot 3 \cdot 2 \cdot 1 = 24 $$

Pentagono

$$ | D_5 | = 10 $$

$$ | S_5 | = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120 $$

E così via.