Legge di Planck
La legge di Planck descrive l’intensità della radiazione elettromagnetica emessa da un corpo nero in funzione della lunghezza d’onda (o frequenza) e della temperatura, introducendo il concetto di quantizzazione dell’energia e superando i limiti della fisica classica.
In altre parole, la legge afferma che l'energia della radiazione elettromagnetica viene emessa in quantità discrete, chiamate quanti, che oggi identifichiamo con i fotoni.
$$ E = h \nu $$
Dove $ E $ è l'energia di ogni quanto (fotone), $ h $ è la costante di Planck e $ \nu $ è la frequenza della radiazione elettromagnetica.
Ne consegue che più alta è la frequenza della radiazione, maggiore è l'energia cinetica del fotone.
Nota. È la prima teoria quantistica della fisica: introduce il concetto di quanto di energia $ E=hν $ e ha dato inizio allo sviluppo della meccanica quantistica. Spiega fenomeni fondamentali come l'effetto fotoelettrico che sarà poi analizzato da Einstein nel 1905.
Il contesto storico
Alla fine del XIX secolo, la fisica classica non riusciva a spiegare correttamente l'intensità della radiazione emessa da un corpo nero, in particolare per le lunghezze d’onda corte: secondo la legge di Rayleigh-Jeans, l’energia divergeva all’ultravioletto, la cosiddetta "catastrofe ultravioletta".
Cos'è la catastrofe ultravioletta?
La catastrofe ultravioletta è un problema della fisica classica nato alla fine dell'Ottocento, quando si cercava di spiegare la radiazione emessa da un corpo nero, cioè un oggetto ideale che assorbe tutta la luce che riceve e la riemette in base alla sua temperatura.
Secondo le teorie dell’epoca, un corpo nero avrebbe dovuto emettere sempre più energia man mano che la luce diventava più “violetta”, cioè al crescere della frequenza della radiazione elettromagnetica.
In particolare la legge di Rayleigh-Jeans esprimeva la densità spettrale di energia $\rho(\nu, T)$ , ossia l'energia emessa per unità di frequenza
$$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} kT $$
Dove
- $\nu$ è la frequenza della radiazione
- $T$ è la temperatura del corpo
- $k$ è la costante di Boltzmann
- $c$ è la velocità della luce nel vuoto
Poiché la frequenza ( $ \nu $ ) può crescere indefinitamente, la formula implicava che un corpo nero potesse emettere un’energia infinita, un risultato chiaramente assurdo e incompatibile con l’osservazione.
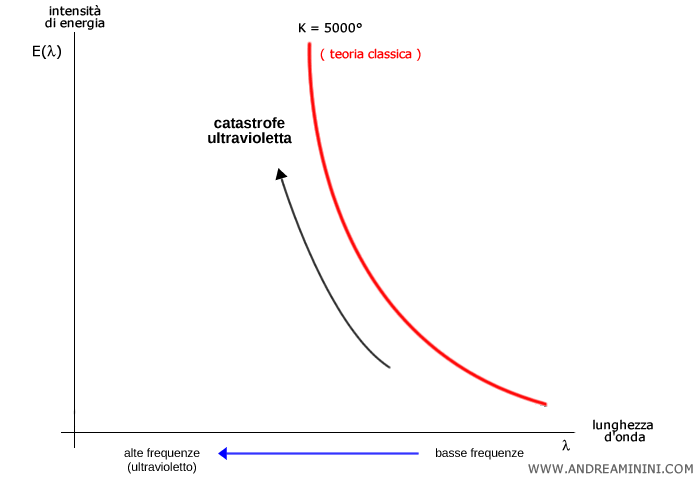
Nella realtà, gli esperimenti mostravano che l’energia emessa da un corpo nero cresceva fino a un valore massimo di frequenza, per poi diminuire alle alte frequenze (ossia alle basse lunghezze d’onda), quando la radiazione si sposta verso l’ultravioletto.
Questo paradosso venne chiamato "catastrofe ultravioletta".
Nota. A quei tempi la radiazione elettromagnetica era considerata esclusivamente un’onda che si propaga nello spazio alla velocità della luce, in accordo con la teoria ondulatoria della luce, che era la visione dominante nella seconda metà dell’Ottocento dopo il trionfo delle equazioni di Maxwell (1860 circa), la luce era vista come un’onda elettromagnetica. In quel quadro, l'energia della radiazione era ritenuta distribuita in modo continuo nello spazio e nel tempo, esattamente come accade in un’onda d’acqua o in un suono. Non c’era alcuna nozione di particelle o di pacchetti discreti di energia.
La soluzione di Planck
Per risolvere il paradosso, nel 1900 il fisico tedesco Max Planck ipotizzò che l’energia della radiazione elettromagnetica $ E $ non fosse continua, ma quantizzata, cioè emessa in pacchetti discreti chiamati quanti:
$$ E = h \nu $$
Dove $\nu$ è la frequenza della radiazione e $ h \approx 6{,}626 \times 10^{-34} \ \text{J·s} $ è una costante matematica usata da Planck per adeguarsi ai dati sperimentali (detta costante di Planck).
Secondo Planck l’energia poteva essere scambiata solo in multipli interi $ n $ di questa quantità elementare:
$$ E = n h \nu \quad \text{con} \quad n = 1, 2, 3, \dots $$
In altre parole, la radiazione non veniva emessa o assorbita in modo continuo, ma solo a "scatti" tramite quantità minime indivisibili (pacchetti di energia o quanti).
Sulla base di questa ipotesi, Planck dedusse una nuova formula per la densità spettrale di energia, oggi nota come legge di Planck:
$$ \rho(\nu, T) = \frac{8 \pi \nu^2}{c^3} \cdot \frac{h\nu}{e^{h\nu/(kT)} - 1} $$
Questa formula descrive con precisione i dati sperimentali osservati.
Alle basse frequenze (cioè alle alte lunghezze d’onda), l’energia emessa aumenta con la frequenza, in accordo con le previsioni della fisica classica.
Tuttavia, superata una certa soglia, alle alte frequenze (basse lunghezze d’onda), l’energia comincia a diminuire, evitando così la catastrofe ultravioletta.
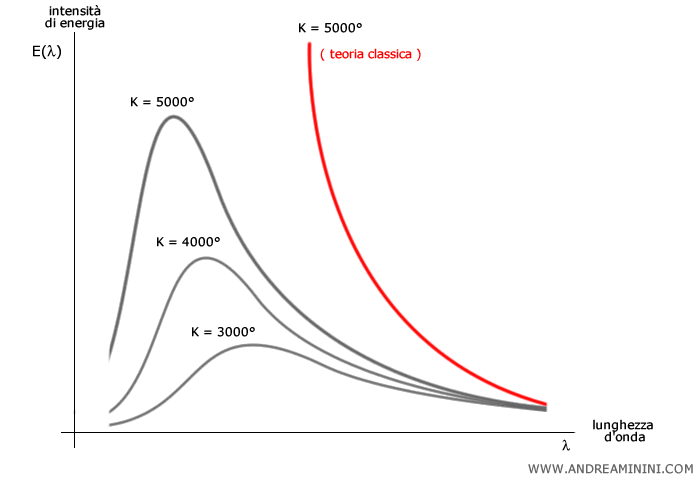
La curva mostra come la distribuzione dell’intensità vari al variare della temperatura assoluta: all’aumentare della temperatura, il picco si sposta verso frequenze maggiori (legge di Wien).
Nota. Una delle grandi forze della legge di Planck è che riproduce la legge di Rayleigh-Jeans alle basse frequenze. Questa è la cosiddetta condizione di corrispondenza tra nuova e vecchia teoria.
Questa formula segnò la nascita della fisica quantistica
L’ipotesi di Planck nel 1900 fu rivoluzionaria perché contraddiceva l’idea di continuità energetica propria del modello ondulatorio.
Pur senza negare che la luce fosse un’onda, Planck introdusse l’idea che l’energia scambiata tra materia e radiazione avvenisse per quanti, cioè in unità discrete.
Fu una rottura epistemologica importante: la luce continuava a comportarsi da onda in molti fenomeni, ma in certi contesti (come l’emissione del corpo nero) sembrava avere anche una natura discreta.
Nota. Va però sottolineato che Planck, inizialmente, non fornì una vera spiegazione fisica del perché la radiazione fosse quantizzata: propose solo l’ipotesi come strumento matematico per far tornare i conti con gli esperimenti.
Un passo oltre: l’effetto fotoelettrico
L’ipotesi dei quanti di Planck trovò conferma decisiva qualche anno dopo grazie all’effetto fotoelettrico, studiato da Einstein nel 1905.
In questo fenomeno, si osserva che la luce incidente su una superficie metallica può causare l’emissione di elettroni solo se la sua frequenza supera una certa soglia, indipendentemente dall’intensità.
Einstein spiegò questo comportamento assumendo che la luce fosse composta da fotoni, ciascuno con energia $E = h\nu$.
Fu la prima vera interpretazione fisica della quantizzazione della radiazione, e segnò un punto di svolta verso la nascita della teoria dei quanti.
E così via.
