Teoria del caos
Cos'è la teoria del caos
La teoria del caos studia il comportamento dei sistemi dinamici caotici. E' un paradigma scientifico elaborato per la prima volta negli anni '60. Riesce a spiegare molti fenomeni naturali altrimenti non spiegabili con l'approccio scientifico deterministico.
Un sistema dinamico è detto sistema caotico quando la sua evoluzione nel tempo dipende dalle condizioni iniziali.
Ad esempio, una successione numerica evolve in modo diverso se cambio il valore iniziale.
Questo comportamento non si può spiegare con il determinismo delle leggi fisiche classiche. E' necessario usare un paradigma diverso.
Nota: caos e caso sono concetti diversi. Il disordine dell'evoluzione di un sistema caotico potrebbe sembrare apparentemente casuale... ma è un errore. In realtà il caso non c'entra affatto con il caos deterministico, perché a parità di valori iniziali un sistema dinamico caotico evolve nello stesso modo e giunge sempre allo stesso risultato finale. E' quindi caoticamente deterministico e prevedibile. Il risultato non è mai casuale.
Il comportamento dei sistemi caotici è spesso indicato come effetto farfalla perché una piccola variazione dei valori iniziali può causare una grande differenza nei risultati finali.
Cos'è l'effetto farfalla?
Una farfalla sbatte le ali in Brasile dando inizio a una serie di fenomeni causa-effetto che si amplificano nel corso del tempo fino a generare un ciclone negli Stati Uniti qualche mese dopo.
La storia dell'effetto farfalla
Il primo ad accorgersi dell'effetto farfalla in alcuni sistemi dinamici (non tutti) fu il matematico e meteorologo statunitense Edward Lorenz negli anni '60.
Nel 1961 Lorenz costruì un modello matematico per prevedere le variazioni atmosferiche.
Elaborò una simulazione inserendo variabili iniziali a 6 cifre decimali (es. 0,314821) e giunse a un risultato.
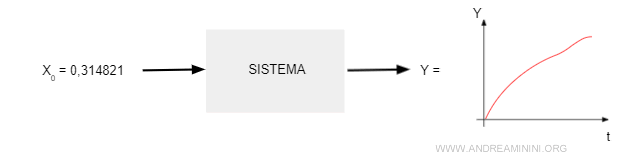
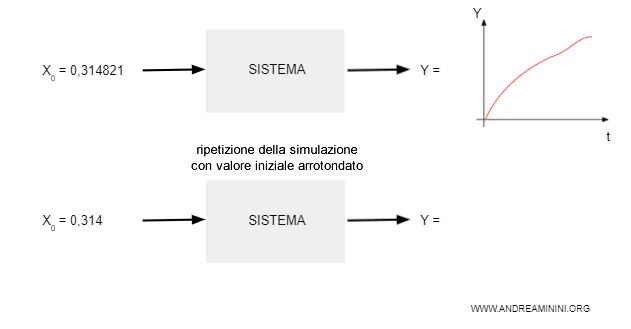
Per risparmiare tempo fece una verifica ripetendo la simulazione con le stesse variabili iniziali arrotondate a 3 cifre decimali (es. 0,314).
In pratica, elaborò la ripetizione della simulazione con un livello di precisione minore. Questo avrebbe accelerato il computo dei calcoli.
Nota. Nel 1961 gli elaboratori elettronici erano macchine di calcolo automatico molto lente. Elaborare calcoli su 3 cifre decimali anziché 6 cifre decimali riduceva il tempo di elaborazione di diverse ore.
Lorenz si aspettava di ottenere lo stesso risultato o perlomeno un risultato simile.
Con sua grande sorpresa il modello giunse a un risultato molto diverso dal precedente. E non era un errore...
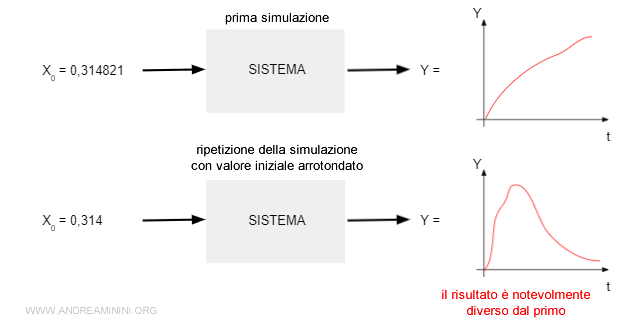
Lorenz si accorse che il modello giungeva correttamente a risultati molto diversi quando usava gli stessi valori iniziali arrotondati.
Nel 1963 Lorenz descrisse l'esperimento in un articolo scientifico "Deterministic Nonperiodic Flow" pubblicato sul Journal of the Atmospheric Sciences.
Questo articolo è considerato la pietra angolare della teoria del caos o teoria del caos deterministico.
Tuttavia, l'articolo di Lorenz del 1963 venne ignorato dagli altri meteorologi.
L'effetto farfalla divenne popolare nella comunità scientifica circa dieci anni dopo per le sue ampie applicazioni multidisciplinari.
Negli anni '70 e '80 la teoria del caos venne usata con discreto successo per spiegare sistemi caotici in vari ambiti scientifici al di fuori della meteorologia (fisica, biologia, matematica, ecc.).
I modelli caotici dimostrarono di avere una buona capacità previsionale di alcuni fenomeni naturali.
In particolar modo nella spiegazione dei sistemi complessi ...ma non solo.
Nota. La teoria del caos ha avuto diverse applicazioni anche nelle scienze sociali ed economiche. Nel tempo ci si rese conto che anche alcuni sistemi semplici possono manifestare una dinamica caotica.
In generale, in alcuni sistemi un piccolo errore nelle condizioni iniziali genera un risultato completamente diverso.
La dinamica caotica di alcuni sistemi produce traiettorie che soltanto inizialmente sono simili.
Nel corso del tempo le traiettorie divergono tra loro perché le piccole variazioni nelle condizioni iniziali diventano sempre più grandi.
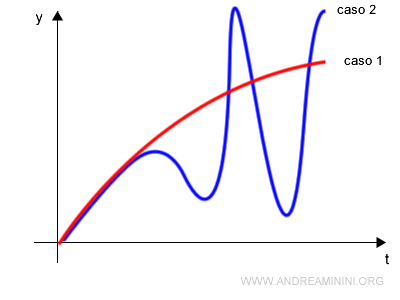
Questo è l'effetto farfalla.
Nota. Fu lo stesso Lorenz a coniare la metafora dell'effetto farfalla. Il matematico statunitense Guckenheimer lo ribattezzò con il termine più scientifico di dipendenza sensibile dalle condizioni iniziali. Il concetto è comunque lo stesso.
Oggi la teoria del caos è conosciuta in modi diversi.
In matematica è detta teoria dei sistemi dinamici, in fisica dinamica non lineare.
In altri ambiti scientifici scienza non lineare.
Per una parte di scienziati la teoria del caos è un campo promettente del sapere, altri scienziati invece la considerano una teoria sopravvalutata
Un esempio pratico
Questa successione numerica ha un comportamento caotico
$$ y_n = 3.7 \cdot y_{(n-1)} \cdot [ \ 1-y_{(n-1)} \ ] $$
perché la sua evoluzione è sensibile al valore iniziale y0.
In questo grafico rappresento i primi dieci termini della successione con due valori iniziali diversi.
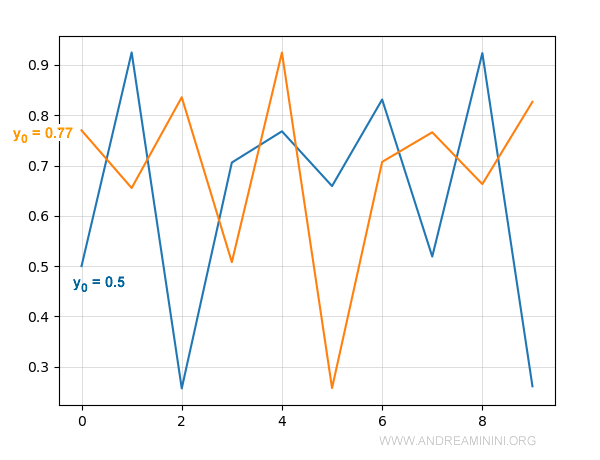
Nel primo caso (linea blu) la successione parte con il valore iniziale y0=0.5 mentre nel secondo caso (linea arancione) con il valore iniziale y0=0.77.
La semplice variazione del valore iniziale causa un comportamento radicalmente diverso.
Questo semplice esempio matematico dovrebbe rendere chiaro il concetto di caos deterministico.
Esempio 2
In ogni caso, non tutti i sistemi dinamici sono sensibili ai valori iniziali.
Ad esempio, questa successione numerica è simile alla precedente, cambia soltanto il coefficiente k=2.1, ma non ha un comportamento caotico
$$ y_n = 2.1 \cdot y_{n-1} \cdot (1-y_{n-1}) $$
Partendo da valori iniziali diversi, y0=0.5 e y0=0.77, la successione evolve in modo diverso.
Tuttavia, nel corso del tempo converge allo stesso risultato finale.
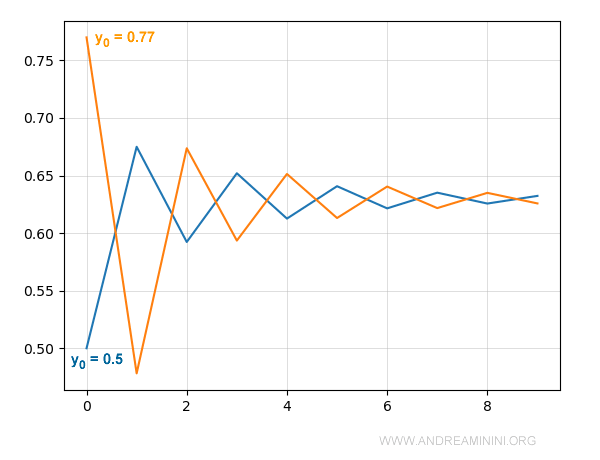
Pertanto, la teoria del caos è utile per spiegare soltanto alcuni fenomeni e sistemi dinamici.
Gran parte dei fenomeni naturali restano ben interpretabili in modo deterministico o probabilistico.
E così via.
