La formula del capacitore nei sistemi elettrici

In un circuito elettrico la formula del capacitore è $$ i = c \dot{v} $$ $$ v = \frac{1}{c} \cdot \int i $$

La spiegazione

La relazione fondamentale di un capacitore (condensatore) è tra la carica elettrica (q) accumulata nella capacità e la tensione (v).

$$ q=cv $$

Usando la convenzione dell'utilizzatore il segno della tensione (v) è positivo.

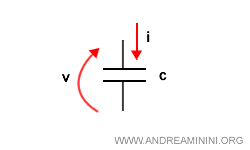
Differenzio l'equazione rispetto al tempo

$$ \frac{dq}{dt} = \frac{dcv}{dt} $$

Sapendo che la derivata della carica elettrica (q) rispetto al tempo è la corrente (i) ossia D[q]=i.

$$ i = \frac{dcv}{dt} $$

Nell'ipotesi che la capacità (c) sia costante

$$ i = c \cdot \frac{dv}{dt} $$

Quindi, la corrente (i) è proporzionale alla derivata della tensione (v)

Nota. Spesso la formula è usata in forma abbreviata. Si omette la variabile di derivazione (t) e si inserisce un punto sopra la variabile derivata prima. $$ i = c \cdot \dot{v} $$ oppure $$ i = c \cdot v' $$

Da questa formula ottengo l'altra

$$ \frac{dv}{dt} = \frac{i}{c} $$

calcolo l'integrale su entrambi i membri dell'equazione per mettere in evidenza la variabile della tensione (v)

$$ \int \frac{dv}{dt} = \int \frac{i}{c} $$ $$ v = \frac{1}{c} \cdot \int i $$

Nota. In alcuni testi l'integrale indefinito è indicato con il simbolo dell'inversa della derivata D^-1 $$ v = \frac{1}{c} \cdot D^{-1}[i] $$

E così via