Esercizio 1 studio del circuito
Devo studiare questo circuito e individuare la potenza sui resistori.
Il circuito è composto da tre generatori indipendenti di tensione e un generatore controllato di corrente.
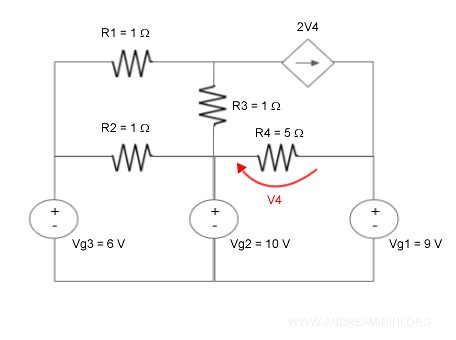
Ci sono varie strade per trovare la tensione e la corrente nei rami del circuito e quindi la potenza sui resistori.
Provo a risolverlo con il metodo degli anelli.
La difficoltà sta nel fatto che
- c'è un generatore controllato di corrente
- non tutti i rami sono Thevenin trasformabili
Quindi la soluzione non si ottiene semplicemente risolvendo il sistema di equazioni.
Il circuito è composto da quattro anelli.
Scelgo arbitariamente il verso orario di percorrenza della corrente di anello in ciascun anello.
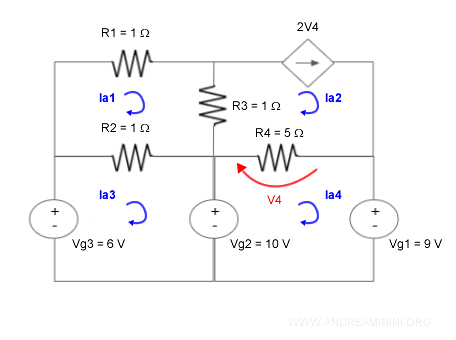
Scrivo il sistema direttamente in forma matriciale canonica
$$ [R_a] \cdot [I_a] = [V_a] $$
Dove [Ra] è la matrice delle resistenze di anello, [Ia] è il vettore delle correnti di anello e [Va] è il vettore delle tensioni di anello.
Le correnti di anello sono quattro e sono le incognite del sistema
$$ [R_a] \cdot \begin{pmatrix} Ia1 \\ Ia2 \\ Ia3 \\ Ia4 \end{pmatrix} = [V_a] $$
La matrice delle resistenze è una matrice quadrata 4x4 in cui ogni colonna/riga è un anello.
Ad esempio, la prima riga e colonna indicano l'anello Ia1, la seconda riga e colonna indicano l'anello Ia2, ecc.
Nella diagonale principale della matrice scrivo le autoresistenze, ossia le resistenze presenti nell'anello
$$ \begin{pmatrix} R1+R2+R3 & & & \\ & R3+R4 & & \\ & & R2 & \\ & & & R4 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia2 \\ Ia3 \\ Ia4 \end{pmatrix} = [V_a] $$
Ad esempio, il primo elemento della diagonale corrisponde alla prima riga e colonna, ossia alle resistenze nell'anello 1. E via dicendo.
Negli altri elementi della matrice scrivo con il segno cambiato le resistenze presenti nei rami condivisi tra due anelli.
$$ \begin{pmatrix} R1+R2+R3 & -R3 & -R2 & 0 \\ -R3 & R3+R4 & 0 & -R4 \\ -R2 & 0 & R2 & 0 \\ 0 & -R4 & 0 & R4 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia2 \\ Ia3 \\ Ia4 \end{pmatrix} = [V_a] $$
Infine, scrivo nel vettore [Va] le tensioni di anello ossia i termini noti del problema.
$$ \begin{pmatrix} R1+R2+R3 & -R3 & -R2 & 0 \\ -R3 & R3+R4 & 0 & -R4 \\ -R2 & 0 & R2 & 0 \\ 0 & -R4 & 0 & R4 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia2 \\ Ia3 \\ Ia4 \end{pmatrix} = \begin{pmatrix} 0 \\ v_{gc} \\ V_{g3} - V_{g2} \\ V_{g2} - V_{g1} \end{pmatrix} $$
$$ \begin{pmatrix} R1+R2+R3 & -R3 & -R2 & 0 \\ -R3 & R3+R4 & 0 & -R4 \\ -R2 & 0 & R2 & 0 \\ 0 & -R4 & 0 & R4 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia2 \\ Ia3 \\ Ia4 \end{pmatrix} = \begin{pmatrix} 0 \\ v_{gc} \\ 6 - 10 \\ 10 - 9 \end{pmatrix} $$
$$ \begin{pmatrix} R1+R2+R3 & -R3 & -R2 & 0 \\ -R3 & R3+R4 & 0 & -R4 \\ -R2 & 0 & R2 & 0 \\ 0 & -R4 & 0 & R4 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia2 \\ Ia3 \\ Ia4 \end{pmatrix} = \begin{pmatrix} 0 \\ v_{gc} \\ - 4 \\ 1 \end{pmatrix} $$
C'è però un problema, la tensione sul generatore di corrente controllato dell'anello 2 non la conosco.
Pertanto Vgc è un'incognita, non è un termine noto.
Inoltre, il sistema ha 4 equazioni e 5 incognite. Quindi devo introdurre delle equazioni di vincolo per ridurre il numero delle incognite.
Guardando il circuito mi accorgo che la tensione pilota v4 posso calcolarla con la legge di Kirchhoff delle tensioni (KVL) sul quarto anello.
$$ V_{g2} - v_4 - V_{g1} = 0 \\ 10 - v_4 - 9 = 0 \\ v_4 = 1 \ V $$
Una volta trovata la tensione pilota V4=1 V posso calcolare la corrente del generatore di corrente controllato
$$ i_{gc} = 2 \cdot V_4 = 2 \cdot 1 = 2 \ A $$
La corrente igc=2 A si trova sul ramo isolato dell'anello 2. Quindi coincide con la corrente Ia2.
$$ Ia2 = I_{gc} = 2 \ A $$
In questo modo ho ridotto le incognite del sistema da cinque a quattro.
$$ \begin{pmatrix} R1+R2+R3 & -R3 & -R2 & 0 \\ -R3 & R3+R4 & 0 & -R4 \\ -R2 & 0 & R2 & 0 \\ 0 & -R4 & 0 & R4 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ 2 \\ Ia3 \\ Ia4 \end{pmatrix} = \begin{pmatrix} 0 \\ v_{gc} \\ - 4 \\ 1 \end{pmatrix} $$
Devo però aggiustare il sistema perché ora non è più in forma canonica. Nei termini noti c'è un'incognita (Vgc) e nelle incognite c'è un termine noto (Ia2=2 A).
Per farlo ricorro alla combinazione lineare tra la matrice [R] e il vettore [I].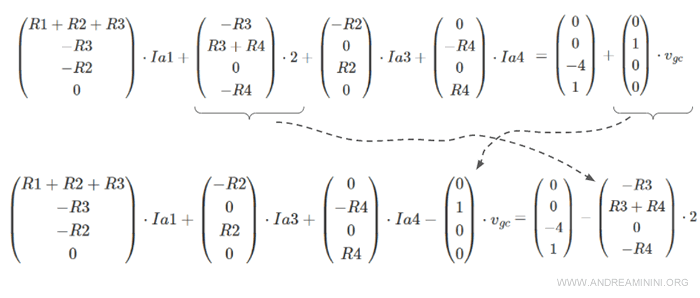
In questo modo posso spostare il vettore con l'incognita Vgc nel membro di sinistra e il vettore Ia2 nel membro di destra.
Poi ricompongo il sistema
$$ \begin{pmatrix} R1+R2+R3 & -R2 & 0 & 0 \\ -R3 & 0 & -R4 & 1 \\ -R2 & R2 & 0 & 0 \\ 0 & 0 & R4 & 0 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia3 \\ Ia4 \\ Vgc \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ - 4 \\ 1 \end{pmatrix} - \begin{pmatrix} -R3 \\ R3+R4 \\ 0 \\ -R4 \end{pmatrix} \cdot 2 $$
Poiché conosco i valori di R1, R2, R3 e R4 posso sostituirli nel sistema.
$$ \begin{pmatrix} 1+1+1 & -1 & 0 & 0 \\ -1 & 0 & -5 & -1 \\ -1 & 1 & 0 & 0 \\ 0 & 0 & 5 & 0 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia3 \\ Ia4 \\ Vgc \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ - 4 \\ 1 \end{pmatrix} - \begin{pmatrix} -1 \\ 1+5 \\ 0 \\ -5 \end{pmatrix} \cdot 2 $$
$$ \begin{pmatrix} 3 & -1 & 0 & 0 \\ -1 & 0 & -5 & -1 \\ -1 & 1 & 0 & 0 \\ 0 & 0 & 5 & 0 \end{pmatrix} \cdot \begin{pmatrix} Ia1 \\ Ia3 \\ Ia4 \\ Vgc \end{pmatrix} = \begin{pmatrix} 2 \\ -12 \\ - 4 \\ 11 \end{pmatrix} $$
Ora il sistema è in forma canonica.
Posso risolverlo con un metodo qualsiasi. In questo caso uso il metodo di Cramer.
Il determinante della matrice dei coefficienti è
$$ \Delta = det \begin{pmatrix} 3 & -1 & 0 & 0 \\ -1 & 0 & -5 & -1 \\ -1 & 1 & 0 & 0 \\ 0 & 0 & 5 & 0 \end{pmatrix} = -10 $$
Gli altri determinanti sono
$$ \Delta Ia1 = det \begin{pmatrix} 2 & -1 & 0 & 0 \\ -12 & 0 & -5 & -1 \\ -4 & 1 & 0 & 0 \\ 11 & 0 & 5 & 0 \end{pmatrix} = 10 $$
$$ \Delta Ia3 = det \begin{pmatrix} 3 & 2 & 0 & 0 \\ -1 & -12 & -5 & -1 \\ -1 & -4 & 0 & 0 \\ 0 & 11 & 5 & 0 \end{pmatrix} = 50 $$
$$ \Delta Ia4 = det \begin{pmatrix} 3 & -1 & 2 & 0 \\ -1 & 0 & -12 & -1 \\ -1 & 1 & -4 & 0 \\ 0 & 0 & 11 & 0 \end{pmatrix} = -22 $$
$$ \Delta Vgc = det \begin{pmatrix} 3 & -1 & 0 & 2 \\ -1 & 0 & -5 & -12 \\ -1 & 1 & 0 & -4 \\ 0 & 0 & 5 & 11 \end{pmatrix} = -20 $$
Quindi, le soluzioni del sistema sono
$$ Ia1 = \frac{ \Delta Ia1 }{ \Delta } = \frac{10}{-10} = -1 \ A $$
$$ Ia3 = \frac{ \Delta Ia3 }{ \Delta } = \frac{50}{-10} = -5 \ A $$
$$ Ia4 = \frac{ \Delta Ia4 }{ \Delta } = \frac{-22}{-10} = 2.2 \ A $$
$$ Vgc = \frac{ \Delta Vg }{ \Delta } = \frac{-20}{-10} = 2 \ A $$
In questo modo ho tutte le altri correnti di anello e la tensione del generatore controllato.
Le correnti di anello mi sono utili per calcolare le correnti in ciascun ramo del circuito.
$$ i1 = Ia1 = -1 \ A $$
$$ i2 = Ia1 - Ia3 = -1 - (-5) = -4 \ A $$
$$ i3 = Ia1 - Ia2 = -1 - 2 = -3 \ A $$
$$ i4 = Ia2 - Ia4 = 2 - 2.2 = -0.2 \ A $$
Con la legge di Ohm calcolo le relative tensioni sui resistori
$$ v1 = R1 \cdot i_1 = 1 \cdot (-1) = -1 \ V $$
$$ v2 = R2 \cdot i_2 = 1 \cdot (-4) = -4 \ V $$
$$ v3 = R3 \cdot i_3 = 1 \cdot (-3) = -3 \ V $$
$$ v4 = R4 \cdot i_4 = 5 \cdot (-0.2) = -1 \ V $$
La potenza del resistore R1 è
$$ P_{R1} = v_1 \cdot i_1 = (-1) \cdot (-1) = 1 \ W $$
$$ P_{R2} = v_2 \cdot i_2 = (-4) \cdot (-4) = 16 \ W $$
$$ P_{R3} = v_3 \cdot i_3 = (-3) \cdot (-3) = 9 \ W $$
$$ P_{R4} = v_4 \cdot i_4 = (-1) \cdot (-0.2) = \frac{1}{5} \ W $$
E così via.
