Condensatore
Il condensatore è un bipolo passivo in grado di immagazzinare energia restituendola in istanti successivi.
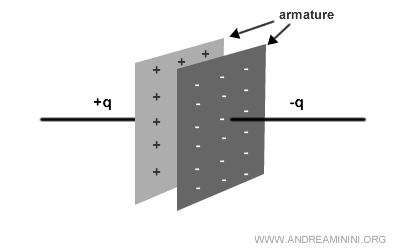
L'energia viene accumulata in un campo elettrico tra due armature metalliche, separate tra loro da un materiale isolante (dielettrico) o dal vuoto.
Generalmente le armature sono di alluminio mentre il dielettrico è un composto di ceramica, carta, polistirolo o aria.
Il parametro del condensatore è la capacità (C) che misura la quantità di cariche accumulate nel bipolo. Si misura in farad (F).
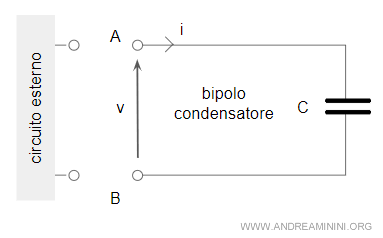
Il condensatore è uno degli elementi conservativi e con memoria di un circuito.
Nota. Si dice conservativo perché può accumulare energia, con memoria perché il suo comportamento dipende dal suo stato.
Come funziona il condensatore
Quando viene collegato a un generatore di tensione, il condensatore accumula cariche positive q in un'armatura e cariche negative -q nell'altra armatura.

Nota. Complessivamente il condensatore è neutro. Pertanto, la somma delle cariche accumulate è sempre nulla.
La carica elettrica immagazzinata dal condensatore in un armatura è direttamente proporzionale alla sua capacità C e alla tensione v.
$$ q = C \cdot v $$
La capacità del condensatore si misura in farad (F).
Nota. Dove 1 farad è uguale a 1 coulumb/volt. L'unità di misura prende il nome di Michael Faraday.
La capacità è un valore indipendente dalla tensione v e dalla carica q, perché dipende esclusivamente dalle caratteristiche fisiche del condensatore (es. dimensione, ampiezza delle armature, distanza tra le armature, costante dielettrica del materiale isolante fra le armature).
$$ C = \frac{\epsilon \cdot A}{d} $$
Pertanto, la capacità del condensatore è una costante.
Le leggi costitutive del condensatore
Le leggi costitutive del condensatore sono $$ i = C \cdot \frac{dv}{dt} $$ $$ v(t) = \frac{1}{C} \int_{t_0}^{t} \:i \: dt + v(t_0) $$
Dimostrazione
Per ottenere le leggi costitutive del condensatore che mettono in relazione la corrente (i) e la tensione (v), parto dalla sua legge fisica.
$$ q = C \cdot v $$
La quantità di carica del condensatore dipende dalla sua capacità e dalla tensione tra le armature.
Derivo entrambi i membri dell'equazione rispetto al tempo.
$$ \frac{dq}{dt} = \frac{d(C \cdot v)}{dt} $$
La derivata delle cariche elettriche nel tempo determina il flusso della corrente, quindi la variabile i=dt/dt
$$ i = \frac{d(C \cdot v)}{dt} $$
Al secondo membro svolgo la derivata del prodotto, ricordandomi che la capacità C è una costante quindi la sua derivata dC/dt=0 è nulla.
$$ i = \frac{dC}{dt} \cdot v + C \cdot \frac{dv}{dt} $$
$$ i = 0 \cdot v + C \cdot \frac{dv}{dt} $$
$$ i = C \cdot \frac{dv}{dt} $$
Ho così ottenuto la relazione corrente-tensione di un condensatore lineare.
Nei condensatori lineari la relazione corrente-tensione è una linea retta.
Nota. Esistono anche condensatori non lineari che non rispettano la precedente legge costitutiva. Nei condensatori non lineari la relazione tra corrente e tensione è una linea curva.
Per trovare la relazione tensione-corrente metto in evidenza la tensione.
$$ i = C \cdot \frac{dv}{dt} $$
$$ \frac{dv}{dt} = \frac{i}{C} $$
Poi integro entrambi i membri tra un istante iniziale t0 e un generico istante t di un intervallo di tempo.
$$ \int_{t_0}^{t} \frac{dv}{dt} dt = \int_{t_0}^{t} \frac{i}{C} dt $$
L'integrale della derivata dv/dt è la tensione v(t)-v(t0) $$
$$ v(t) - v(t_0) = \int_{t_0}^{t} \frac{i}{C} dt $$
Al secondo membro la capacità C è una costante. Quindi, può uscire dall'integrale.
$$ v(t) - v(t_0) = \frac{1}{C} \int_{t_0}^{t} \:i \: dt $$
Sposto la tensione iniziale v(t0) al secondo membro.
$$ v(t) = \frac{1}{C} \int_{t_0}^{t} \:i \: dt + v(t_0) $$
In questo modo ottendo la legge costitutiva tensione-corrente del condensatore.
Nota. La tensione v(t0) al tempo t0 è la memoria del condensatore perché dipende dai suoi stati passati.
La potenza del condensatore
La potenza del condensatore varia nel tempo.
Pertanto, si parla di potenza istantanea del condensatore in un determinato istante t.
$$ p = v \cdot i $$
Sostituisco la corrente i con la sua legge costitutiva.
$$ p = v \cdot C \frac{dv}{v} $$
Per calcolare la potenza W accumulata dal condensatore in un intervallo di tempo (t0,t) calcolo l'integrale definito.
$$ W = \int_{t_0}^t p \: dt $$
$$ W = \int_{t_0}^t v \cdot C \frac{dv}{v} \: dt $$
$$ W = C \cdot \int_{t_0}^t v \frac{dv}{v} \: dt $$
La primitiva dell'integrale 1/2v2.
$$ W = C \cdot [ \frac{1}{2} \cdot v^2 ]^t_{t_0} $$
$$ W = C \cdot ( \frac{1}{2} \cdot v^2(t) - \frac{1}{2} \cdot v^2(t_0) ) $$
Per semplicità ipotizzo che il condensatore era scarico nel momento iniziale t0. Quindi v(t0)=0.
$$ W = C \cdot \frac{1}{2} \cdot v^2(t) $$
o semplicemente
$$ W = \frac{1}{2} C \cdot v^2 $$
Questa formula calcola l'energia accumulata tra le armature del condensatore nell'intervallo di tempo.
Nota. Quest'ultima formula posso scriverla anche in termini di cariche elettriche. $$ W = \frac{q^2}{2C}$$ Per dimostrarlo basta ricordarsi la legge q=Cv da cui ricavo la tensione v=q/C. Sostituisco la tensione nella formula della potenza. $$ W = C \cdot \frac{1}{2} \cdot v^2 $$ $$ W = C \cdot \frac{1}{2} \cdot (\frac{q}{C})^2 $$ poi semplifico $$ W = C \cdot \frac{1}{2} \cdot \frac{q^2}{C^2} $$ $$ W = \frac{1}{2} \cdot \frac{q^2}{C} $$ $$ W = \frac{q^2}{2C} $$
Osservazioni sul condensatore
Alcune osservazioni utili sul comportamento di un condensatore ideale.
- Un condensatore ideale non dissipa energia. La potenza assorbita viene restituita al circuito.
- Le variazioni di tensione su un condensatore non possono essere istantanee. Avvengono progressivamente nel tempo.
- Le variazioni di corrente su un condensatore possono essere istantanee.
- Quando sul condensatore la tensione è costante, il condensatore è carico e la corrente è nulla (non passa).
- Se la corrente è continua il condensatore si comporta come un bipolo circuito aperto.
E così via.
