Analisi nodale per ispezione

L'analisi nodale del circuito elettrico può essere ottenuta per ispezione, se sono presenti soltanto generatori indipendenti di corrente.

1. Considero i resistori R del circuito come conduttanze G
2. Creo la matrice delle conduttanze $$ \begin{pmatrix} G_{1,1} & ... & G_{1,n} \\ \vdots & \ddots & \vdots \\ G_{n,1} & ... & G_{n,n} \end{pmatrix} $$ Dove n è il numero di nodi non di riferimento del circuito elettrico.
   1. Sulla diagonale principale indico la somma delle conduttanze collegate ai nodi da 1 a n.
   2. Sui nodi j,k indico la somma delle conduttanze tra il nodo i e il nodo j cambiato di segno.
   Poi aggiungo la colonna delle tensioni e delle correnti degli n nodi. $$ \begin{pmatrix} G_{1,1} & ... & G_{1,n} & v_1 & i_1 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ G_{n,1} & ... & G_{n,n} & v_n & i_n \end{pmatrix} $$

Un esempio

Ho il seguente circuito con due generatori di corrente indipendenti (I₁ e I₂) e due nodi non di riferimento (v₁ e v₂).

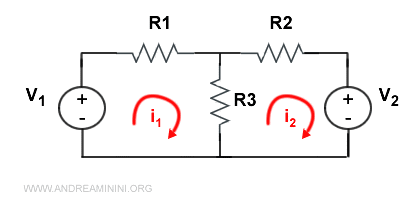
Comincio a scrivere la matrice delle conduttanze per n=2 nodi.

$$ \begin{pmatrix} -- & -- & v_1 & -- \\ -- & -- & v_2 & -- \end{pmatrix} $$

Nell'elemento a_1,1 digito la somma delle conduttanze G₁+G₂ del nodo v₁.

$$ \begin{pmatrix} G_1+G_2 & -- & v_1 & -- \\ -- & -- & v_2 & -- \end{pmatrix} $$

Nell'elemento a_2,2 digito la somma delle conduttanze G₂+G₃ del nodo v₂.

$$ \begin{pmatrix} G_1+G_2 & -- & v_1 & -- \\ -- & G_2+G_3 & v_2 & -- \end{pmatrix} $$

La diagonale principale dei nodi è completa. Ora posso inserire i dati dei singoli rami.

Nell'elemento a_1,2 inserisco la somma delle conduttanze tra il nodo v₁ e il nodo v₂ cambiato di segno.

$$ \begin{pmatrix} G_1+G_2 & -G_2 & v_1 & -- \\ -- & G_2+G_3 & v_2 & -- \end{pmatrix} $$

Nell'elemento a_2,1 scrivo la somma delle conduttanze tra il nodo v₂ e il nodo v₁ cambiato di segno.

$$ \begin{pmatrix} G_1+G_2 & -G_2 & v_1 & -- \\ -G_2 & G_2+G_3 & v_2 & -- \end{pmatrix} $$

Nell'ultima colonna inserisco le correnti (I₁-I₂) del nodo v₁.

$$ \begin{pmatrix} G_1+G_2 & -G_2 & v_1 & I_1-I_2 \\ -G_2 & G_2+G_3 & v_2 & -- \end{pmatrix} $$

Nella seconda riga dell'ultima colonna digito le correnti (I₂) del nodo v₂.

$$ \begin{pmatrix} G_1+G_2 & -G_2 & v_1 & I_1-I_2 \\ -G_2 & G_2+G_3 & v_2 & I_2 \end{pmatrix} $$

Essendo già noti i valori delle conduttanze G e delle correnti i, posso facilmente trovare le tensioni (v) risolvendo il sistema di equazioni.

$$ \begin{pmatrix} G_1+G_2 & -G_2 \\ -G_2 & G_2+G_3 \end{pmatrix} \begin{pmatrix} v_1 \\ v_2 \end{pmatrix} = \begin{pmatrix} I_1-I_2 \\ I_2 \end{pmatrix} $$

E così via.