Analisi nodale

L'analisi nodale di un circuito elettrico misura la tensione nei nodi anziché sugli elementi.

Qual è il vantaggio dell'analisi nodale?

Il numero di equazioni matematiche per rappresentare il circuito tramite i nodi è inferiore.

Come funziona

Dato un circuito l'analisi nodale consiste nei seguenti passi:

1. Scelgo un nodo di riferimento o di massa. E' indicato come nodo 0 (v=0) e con uno dei seguenti simboli.
   

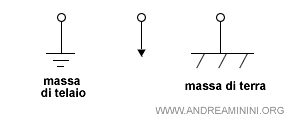
   E' detto nodo di massa perché è considerato a potenziale zero. Nella massa di telaio (chassis ground) si usa il telaio dell'apparecchiatura. Nella massa di terra (earth ground) si usa il suolo.

2. Assegno le tensioni v_n agli n-1 nodi restanti rispetto al nodo di riferimento
3. Applico la legge di Kirchhoff (KCL) e la legge di Ohm agli n-1 nodi
4. Risolvo le equazioni per calcolare le tensioni di nodo

Un esempio pratico

Devo studiare le tensioni e le correnti in questo circuito tramite l'analisi nodale

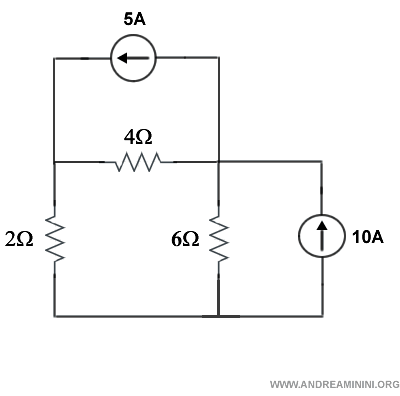
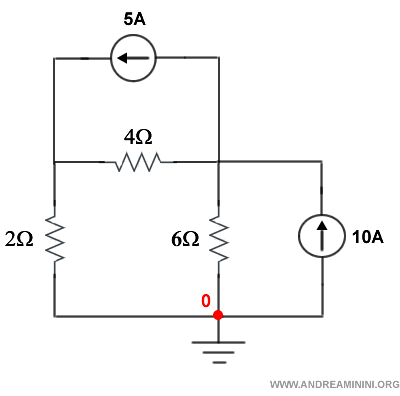
Scelgo come nodo di riferimento il primo nodo in basso.

Gli assegno il numero 0. E' il nodo con potenziale nullo ossia v₀=0.

Assegno ai restanti nodi del circuito elettrico le incognite v₁ e v₂.

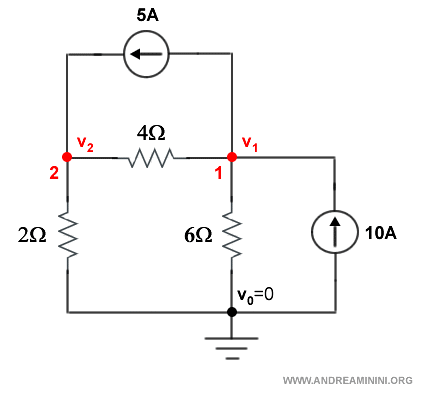
Seguo il flusso della corrente e assegno le incognite i ai rami.

Nel caso di i₁ e i₄ conosco già i valori da assegnare tramite i rispettivi generatori.

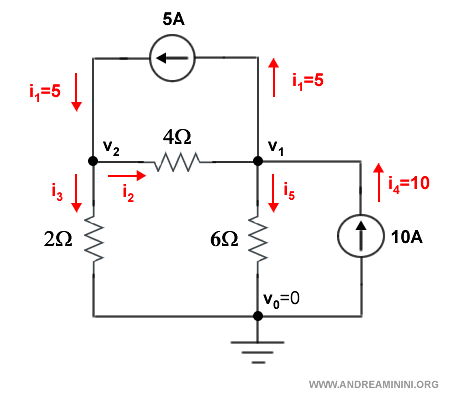
A questo punto, usando la legge di Kirchhoff sulle correnti (KCL) posso scrivere le equazioni del nodo 1

$$ i_4 + i_2 = i_1+i_5 $$

e del nodo 2

$$ i_1 = i_2+i_3 $$

Sostituisco i valori che già conosco i₁=5 e i₄=10.

$$ 5 = i_2+i_3 $$

$$ 10 + i_2 = 5+i_5 $$

Ora uso la legge di Ohm per riscrivere le formule della corrente i₂, i₃ e i₅.

$$ i_2 = \frac{v}{R} = \frac{v}{4} $$

$$ i_3 = \frac{v}{R} = \frac{v}{2} $$

$$ i_5 = \frac{v}{R} = \frac{v}{6} $$

Sapendo in un resistore la tensione passa da un valore iniziale alto a uno più basso in uscita.

$$ i = \frac{v_{In}-v_{Out}}{R} $$

posso riscrivere le formule della corrente

$$ i_2 = \frac{v_2-v_1}{4} $$

$$ i_3 = \frac{v_2-v_0}{2} = \frac{v_2-0}{2} = \frac{v_2}{2} $$

$$ i_4 = \frac{v_1-v_0}{6} = \frac{v_1-0}{6} = \frac{v_1}{6} $$

Ora sostituisco le formule della corrente nelle equazioni del circuito

$$ \begin{cases} 5 = i_2+i_3 \\ 10 + i_2 = 5+i_5 \end{cases} $$

$$ \begin{cases} 5 = \frac{v_2-v_1}{4}+ \frac{v_2}{2} \\ 10 + \frac{v_2-v_1}{4} = 5+\frac{v_1}{6} \end{cases} $$

$$ \begin{cases} 20 = 3v_2-v_1 \\ 60 = 5v_1-3v_2 \end{cases} $$

Poi trovo i valori delle incognite v₁ e v₂ risolvendo il sistema di equazioni con il metodo della sostituzione o di Cramer.

$$ \begin{cases} v_1 = 20 \\ v_2 = \frac{40}{3} \end{cases} $$

Una volta trovati i valori delle tensioni, posso calcolare anche le correnti

$$ i_2 = \frac{v_2-v_1}{4} = \frac{\frac{40}{3}-20}{4} = - \frac{5}{3} $$

$$ i_3 = \frac{v_2}{2} = \frac{\frac{40}{3}}{2} = \frac{20}{3} $$

$$ i_4 = \frac{v_1}{6} = \frac{20}{6} = \frac{10}{3} $$

Ho così trovato tutti i dati del circuito elettrico.

E così via.