La formula fondamentale del calcolo integrale

L'integrale definito della funzione integranda f(x) nell'intervallo di integrazione [a,b] è uguale alla differenza della funzione primitiva F(x) calcolata agli estremi dell'integrale. $$ \int_a^b f(x) \:\:dx = F(b)-F(a) $$

Cos'è la funzione primitiva?

Una funzione primitiva F(x) è una funzione che derivata dia come risultato la funzione integranda f(x).

Nota. Non è sempre semplice trovare la primitiva della funzione integranda f(x). Tuttavia, se è possibile, il calcolo dell'integrale di una funzione diventa molto semplice.

Un esempio pratico

Devo calcolare l'integrale seguente:

$$ \int_2^6 3x^2 \:\: dx $$

La primitiva F(x) della funzione f(x) è

$$ F(x) = x^3 $$

perché la sua derivata prima F'(x) è uguale alla f(x)

$$ D [ x^3 ] = 3x^2 $$

Pertanto, l'integrale definito della funzione f(x) nell'intervallo [2,6] è

$$ \int_2^6 3x^2 \:\: dx = F(6) - F(2) = (6)^3 - (2)^3 = 208 $$

E' l'area compresa tra il grafico e l'asse delle ascisse.

La dimostrazione

Prendo in considerazione due primitive F(x) e G(x) della continua f(t) nell'intervallo [a,x].

$$ G(x) = \int_a^x f(t) \: dt $$

$$ F(x) = \int_a^x f(t) \: dt $$

Secondo una proprietà delle primitive, due primitive F(x) e G(x) della stessa funzione f(x) si distinguono tra loro per una costante k.

$$ G(x)-F(x) = k $$

ossia

$$ G(x) = F(x) + k $$

$$ G(x) = k + \int_a^x f(t) \: dt $$

Calcolo l'integrale per x=a

$$ G(a) = k + \int_a^a f(t) \: dt $$

$$ G(a) = k + 0 $$

$$ G(a) = k $$

Quindi, se k=G(a) posso riscrivere la precedente formula come

$$ G(x) = k + \int_a^x f(t) \: dt $$

$$ G(x) = G(a) + \int_a^x f(t) \: dt $$

Ora, ponendo x=b la formula diventa

$$ G(b) = G(a) + \int_a^b f(t) \: dt $$

e con un semplice passaggio algebrico ottengo

$$ G(b) - G(a) = \int_a^b f(t) \: dt $$

che dimostra la formula fondamentale del calcolo integrale.

Altri esempi pratici

Esempio 1

Il caso più semplice di integrale definito è l'integrale di una funzione costante.

$$ f(x) = k $$

Nell'intervallo [a,b] l'integrale definito della funzione è

$$ \int_a^b f(x) \:\: dx = k \cdot (b-a) $$

Ad esempio, se la funzione costante è 5

$$ f(x) = 5 $$

l'intergrale definito nell'intervallo [2,7] è

$$ \int_2^7 5 \:\: dx = 5 ( 7 - 2 ) = 25 $$

Ecco la rappresentazione grafica

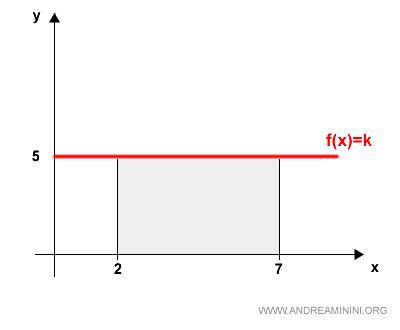
Nota. L'estremo di integrazione superiore (b) non deve essere necessariamente maggiore dell'estremo inferiore (a). Può anche essere minore. In questo caso il risultato dell'integrale ha segno opposto. $$ \int_7^2 5 \:\: dx = 5 ( 2 - 7 ) = - 25 $$ Nel caso in cui gli estremi di integrazione coincidono (a=b) il risultato è nullo. $$ \int_2^2 5 \:\: dx = 5 ( 2 - 2 ) = 0 $$

E così via.