Le leggi dell'algebra booleana
Date tre variabili booleane x,y,z valgono le seguenti leggi dell'algebra booleana.

Molte leggi precedenti sono leggi duali.
Ecco alcune dimostrazioni
Dimostrazione della legge del doppio complemento
Secondo la legge del doppio complemento
$$ x = \overline{\overline{x}} $$
Costruisco la tavola di verità
$$ \begin{array}{c|r|c} x & \overline{x} & \overline{ ( \overline{x} ) } \\ \hline 0 & 1 & 0 & \\ 1 & 0 & 1 \end{array} $$
La tavola dimostra la validità della legge.
La prima e la terza colonna sono identiche.
Dimostrazione delle leggi di De Morgan
Secondo le leggi di De Morgan
$$ \overline{x+y} = \overline{x} \overline{y} \\ \\ \overline{xy} = \overline{x} + \overline{y} $$
Per verificare la validità costruisco la tavole di verità
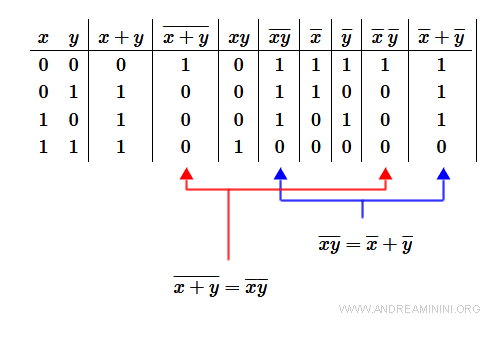
La tavola di verità conferma la validità delle leggi di De Morgan.
Dimostrazione delle leggi di assorbimento
Secondo le leggi di assorbimento.
$$ x+xy = x \\ x(x+y)=x $$
Costruisco la tavola di verità per verificare le leggi.
$$ \begin{array}{cr|c} x & y & xy & x+xy \\ \hline 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{array} $$
La quarta colonna x+xy è uguale alla prima colonna x.
$$ \begin{array}{cr|c} x & y & x+y & x(x+y) \\ \hline 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array} $$
La quarta colonna x(x+y) è uguale alla prima colonna x.
Ho così dimostrato le leggi di assorbimento.
Dimostrazione delle leggi degli inversi
Secondo le leggi degli inversi.
$$ x + \overline{x} = 1 \\ x \cdot \overline{x} = 0 $$
Costruisco la tavola di verità per verificare le leggi.
$$ \begin{array}{c|r|c} x & \overline{x} & x+\overline{x} & x \cdot \overline{x} \\ \hline 0 & 1 & 1 & 0\\ 1 & 0 & 1 & 0 \end{array} $$
La tavola di verità dimostra le leggi degli inversi.
Dimostrazione delle leggi di idempotenza
Le leggi di idempotenza dell’algebra booleana affermano che, per ogni valore logico di $ x $
$$ x + x = x \\ x \cdot x = x $$
Per verificarle, costruisco la tavola di verità:
$$ \begin{array}{c|r|c} x & x & x+x & x \cdot x \\ \hline 0 & 0 & 0 & 0 & \\ 1 & 1 & 1 & 1 \end{array} $$
A colpo d'occhio si vede che, per entrambi i possibili valori di $ x $, le espressioni $ x+x $ e $ x \cdot x $ coincidono sempre con $ x $.
Questo conferma le leggi di idempotenza.
