Le reti di code markoviane chiuse
Le reti di code markoviani chiuse non hanno arrivi dall'esterno. Il numero dei clienti/utenti nella rete di code è costante. $$ λ_{in}=0 \:\: \forall i$$
In questo caso, quando un cliente esce dal sistema, il cliente rientra automaticamente nel sistema.
Pertanto, lo spazio degli stati x (numero degli utenti nel sistema) è un numero finito e costante.
Nota. La rete di code chiusa è detta "markoviana" quando può essere interpretata come una catena di Markov, secondo il teorema di Gordon-Newell.
Come funziona
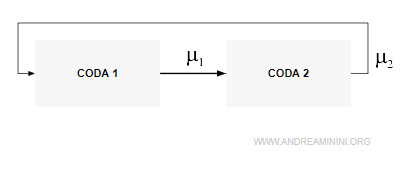
Questa rete tandem è composta da due code in serie.
L'uscita è collegata con l'entrata al sistema tramite un collegamento retroattivo (feedback).

Secondo il teorema di Gordon-Newell
la rete di code chiusa può essere trasformata in una catena di Markov se non esiste al suo interno nessuna sottorete in cui i clienti possano entrare ma non uscire.
Lo spazio degli stati del sistema è
$$ |X| = \begin{pmatrix} v+n-1 \\ n \end{pmatrix} $$
Dove n è il numero dei clienti nel sistema
La distribuzione di probabilità a regime è
$$ π(x_1,...,x_v) = k \cdot \prod_{i=1}^v \frac{α_i^{x_i}}{β(x_i)} $$
$$ π(x_1,...,x_v) = \frac{1}{\sum_{x \in X} (\prod_{i=1}^v \frac{α_i^{x_i}}{β(x_i)} ) } \cdot \prod_{i=1}^v \frac{α_i^{x_i}}{β(x_i)} $$
dove β è
$$ β (x_i) = \begin{cases} x_i! \:\: \text{ se xi < mi } \\ m_i! \cdot m_i^{x_i-m_i} \:\: \text{altrimenti} \end{cases} $$
mentre α sono le soluzioni del sistema omogeneo
$$ α_i \cdot μ_i = \sum_{j=1}^v r_{ij} μ_j α_j $$
dove rij sono gli elementi della matrice di instradamento R.
Un esempio pratico
La rete di code è composta da due code.
La prima coda ha m1=2 servitori e un tempo di servizio μ1.
La seconda coda ha m2=1 servitori e un tempo di servizio μ2.
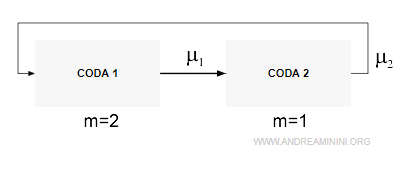
Dato il numero dei servitori (m1+m2=1+2), il numero dei clienti nel sistema è n=3.
La matrice di instradamento R è
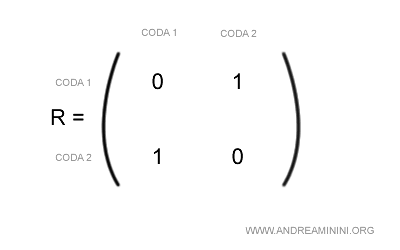
poiché in questo semplice modello di rete chiusa a due code l'uscita da una coda implica al 100% l'ingresso nell'altra coda con una probabilità pari a 1.
Gli stati dei singoli nodi sono rispettivamente x1 e x2
$$ x_1 \in \{ 0,1, 2, 3 \} $$
$$ x_2 \in \{ 0,1, 2, 3 \} $$
Dove x1 indica il numero dei clienti nella prima coda mentre x2 il numero dei clienti nella seconda coda.
In una rete di code chiusa il numero dei clienti è costante. In questo caso è n=3.
$$ x_1 + x_2 = 3 $$
Pertanto, lo spazio degli stati X della rete di code
$$ X = (x_1,x_2) $$
è un insieme finito composto dalle seguenti combinazioni
$$ X = \{ (0,3),(1,2),(2,1),(3,0) \} $$
Prima di calcolare le probabilità di stato a regime del sistema, devo prima ottenere i valori delle funzioni beta e delle costanti alfa.
$$ β (x_i) = \begin{cases} x_i! \:\: \text{ se xi < mi } \\ m_i! \cdot m_i^{x_i-m_i} \:\: \text{altrimenti} \end{cases} $$
La prima coda ha m=2 serventi
$$ β (x_1=0) = 0! = 1 $$
$$ β (x_1=1) = 1! = 1 $$
$$ β (x_1=2) = 2! \cdot 2^{2-2} = 2 \cdot 2^0 = 2 $$
$$ β (x_1=3) = 3! \cdot 2^{3-2} = 2 \cdot 2^1 = 4 $$
La seconda coda ha m=1 serventi
$$ β (x_2=0) = 0! = 1 $$
$$ β (x_2=1) = 1! \cdot 1^{1-1} = 1 \cdot 1^0 = 1 $$
$$ β (x_2=2) = 1! \cdot 1^{2-1} = 1 \cdot 1^1 = 1 $$
$$ β (x_2=3) = 1! \cdot 1^{3-1} = 1 \cdot 1^2 = 1 $$
Le costanti α sono le soluzioni del sistema omogeneo
$$ α_i \cdot μ_i = \sum_{j=1}^v r_{ij} \cdot μ_j \cdot α_j $$
Quindi
$$ \begin{cases} α_1 \cdot μ_1 = r_{11} \cdot μ_1 \cdot α_1 + r_{12} \cdot μ_2 \cdot α_2 \\ α_2 \cdot μ_2 = r_{21} \cdot μ_1 \cdot α_1 + r_{22} \cdot μ_2 \cdot α_2 \end{cases} $$
$$ \begin{cases} α_1 \cdot μ_1 = 0 \cdot μ_1 \cdot α_1 + 1 \cdot μ_2 \cdot α_2 \\ α_2 \cdot μ_2 = 1 \cdot μ_1 \cdot α_1 + 0 \cdot μ_2 \cdot α_2 \end{cases} $$
$$ \begin{cases} α_1 \cdot μ_1 = μ_2 \cdot α_2 \\ α_2 \cdot μ_2 = μ_1 \cdot α_1 \end{cases} $$
Lo risolvo per sostituzione
$$ \begin{cases} α_1 \cdot μ_1 = μ_2 \cdot α_2 \\ α_2 = \frac{μ_1}{μ_2} \cdot α_1 \end{cases} $$
$$ \begin{cases} α_1 \cdot μ_1 = μ_2 \cdot ( \frac{μ_1}{μ_2} \cdot α_1 ) \\ α_2 = \frac{μ_1}{μ_2} \cdot α_1 \end{cases} $$
$$ \begin{cases} α_1 = α_1 \\ α_2 = \frac{μ_1}{μ_2} \cdot α_1 \end{cases} $$
Il sistema è indeterminato.
Assegno a1=1 per semplificarlo.
$$ \begin{cases} α_1 = 1 \\ α_2 = \frac{μ_1}{μ_2} \cdot 1 \end{cases} $$
$$ \begin{cases} α_1 = 1 \\ α_2 = \frac{μ_1}{μ_2} \end{cases} $$
A questo punto posso calcolare la distribuzione delle probabilità a regime tramite la formula
$$ π(x_1,...,x_v) = k \cdot \prod_{i=1}^v \frac{α_i^{x_i}}{β(x_i)} $$
$$ π(x_1,...,x_v) = \frac{1}{\sum_{x \in X} (\prod_{i=1}^v \frac{α_i^{x_i}}{β(x_i)} ) } \cdot \prod_{i=1}^v \frac{α_i^{x_i}}{β(x_i)} $$
Le probabilità degli stati a regime per ogni elemento dello spazio degli stati X sono
$$ π(0,3) = k \cdot \frac{α_1^{x_1}}{β(x_1)} \cdot \frac{α_2^{x_2}}{β(x_2)} = k \cdot \frac{α_1^{0}}{β(x_1=0)} \cdot \frac{α_2^{3}}{β(x_2=3)} = k \cdot \frac{1^{0}}{1} \cdot \frac{( \frac{μ_1}{μ_2})^{3}}{1} = k \cdot ( \frac{μ_1}{μ_2} )^3 $$
$$ π(1,2) = k \cdot \frac{α_1^{x_1}}{β(x_1)} \cdot \frac{α_2^{x_2}}{β(x_2)} = k \cdot \frac{α_1^{1}}{β(x_1=1)} \cdot \frac{α_2^{2}}{β(x_2=2)} = k \cdot \frac{1^{1}}{1} \cdot \frac{( \frac{μ_1}{μ_2})^{2}}{1} = k \cdot ( \frac{μ_1}{μ_2} )^2 $$
$$ π(2,1) = k \cdot \frac{α_1^{x_1}}{β(x_1)} \cdot \frac{α_2^{x_2}}{β(x_2)} = k \cdot \frac{α_1^{2}}{β(x_1=2)} \cdot \frac{α_2^{1}}{β(x_2=1)} = k \cdot \frac{1^{1}}{2} \cdot \frac{( \frac{μ_1}{μ_2})^{1}}{1} = k \cdot \frac{μ_1}{μ_2} $$
$$ π(3,0) = k \cdot \frac{α_1^{x_1}}{β(x_1)} \cdot \frac{α_2^{x_2}}{β(x_2)} = k \cdot \frac{α_1^{3}}{β(x_1=3)} \cdot \frac{α_2^{0}}{β(x_2=0)} = k \cdot \frac{1^{3}}{4} \cdot \frac{( \frac{μ_1}{μ_2})^{0}}{1} = k \cdot \frac{1}{4} $$
Nota. Le probabilità di stato a regime della rete di code non sono uguali alle probabilità di stato a regime delle singole code che la compongono.
E così via
