Le specifiche dinamiche del supervisore
Una specifica dinamica è un sottoinsieme K del linguaggio L dell'automa che indica quali parole sono ammissibili e quali sono proibite.
Pertanto, le specifiche dinamiche generano un linguaggio legale dell'automa.
Le specifiche dinamiche sono usate nei sistemi a eventi discreti (SED) per istruire il supervisore e introdurre un 'attività di controllo.
Le parole ammissibili e proibite
Le parole ammissibili
Sono ammissibili tutte le parole la cui proiezione sull'alfabeto E è una parola del linguaggio legale K.
$$ L || K = \{ w \in L | w \uparrow E* \in K \} $$
Dove E* è l'insieme di tutte le combinazioni dei simboli presenti nell'alfabeto E.
L'insieme delle parole ammissibili è l'intersezione K⋂L.
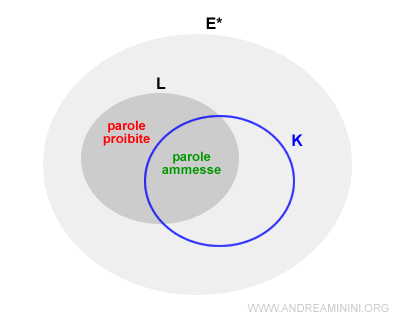
Le parole proibite
Sono proibite tutte le parole la cui proiezione sull'alfabeto E non è una parola del linguaggio legale K.
$$ L || (\text{E*\K}) = \{ w \in L | w \uparrow E \notin K \} $$
Dove E* è l'insieme di tutte le combinazioni dei simboli presenti nell'alfabeto E.
L'insieme delle parole proibite è L\K.
Le specifiche dinamiche totali e parziali
Una specifica dinamica dell'automa può essere
- Specifica dinamica totale
se è composta da tutti i simboli dell'alfabeto E dell'automa. In questo caso non ci sono parole (sequenze di eventi) escluse dal controllo.

- Specifica dinamica parziale
se è composta da un sottoinsieme E' di simboli dell'alfabeto E dell'automa. In tale caso, il supervisore non vincola gli eventi che utilizzano i restanti simboli E'\E dell'alfabeto. Gli altri eventi E'\E possono verificarsi senza alcun controllo.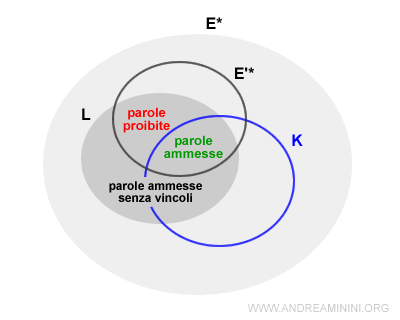
Nota. L'insieme E'* è composto dalle parole formate dalle combinazioni dei simboli dell'alfabeto parziale E'. Ad esempio se E={a,b,c,d} ed E={b,c} allora E'*={b,c,bc,bb,cc,bcb,cbc,...}
Un esempio pratico
Questo automa identifica le operazioni di una stampante.
Ci sono quattro stati X={x0,x1,x2,x3} dove lo stato x0="spenta", x1="accesa", x2="in stampa", x3="senza cartuccia".
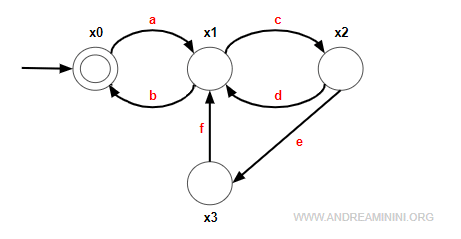
Gli eventi dell'automa sono sei E={a,b,c,d,e,f}.
- a=accendi
- b=spegni
- c=stampa un foglio
- d=finisce la stampa
- e=togli la cartuccia dell'inchiostro
- f=inserisci una nuova cartuccia
Una specifica dinamica parziale obbliga il cambio della cartuccia (w=ef) dopo la stampa di 30 fogli w=(cd)30.
$$ K_1 = \{ w \in E'_* | w = (cd)^{30}ef \} $$
Dove E'={cdef} è un sottoinsieme dell'alfabeto dell'automa e E'* è l'insieme delle parole composte dai simboli di E'.
Gli eventi controllabili e non controllabili dal supervisore
L'insieme degli eventi E è partizionato in eventi controllabili dal supervisore Ec ed evento non controllabili En.
Gli eventi controllabili possono essere disabilitati dal supervisore.
Pertanto, gli eventi attivi ma disabilitabili di uno stato sono l'intersezione tra l'insieme degli eventi attivi A(x) dello stato x e l'insieme degli eventi controllabili Ec
$$ A(x) ⋂ E_c $$
Generalmente, gli eventi controllabili dal supervisore sono indicati nella rappresentazione grafica dell'automa con il simbolo dei due punti : nel suffisso
Esempio. In questo automa l'insieme degli eventi è composto da sei eventi E={a,b,c,d,e,f}. Il supervisore può controllare soltanto gli eventi Ec={e,f} mentre non controlla gli eventi En={a,b,c,d}. Pertanto, l'insieme ha una partizione con due sottoinsiemi
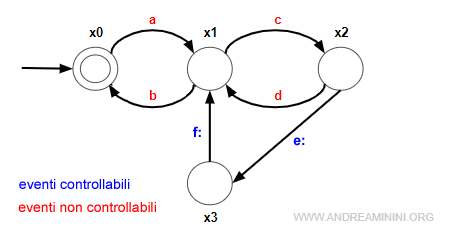
Quando l'automa si trova nello stato x2 gli eventi attivi A(x2)={d,e} si riducono a A(x2)⋂Ec={d} perché il supervisore potrebbe disabilitare o meno l'evento e. Viceversa, l'evento d è sempre attivo perché il supervisore non ha alcun controllo su quest'ultimo.
Il supervisore non può invece intervenire sugli altri eventi attivi detti eventi non controllabili.
$$ A(x) ⋂ E_n $$
Su questi ultimi non ci sono vincoli.
Sono eventi ammissibili nel linguaggio legale dell'automa e non possono essere disabilitati dal supervisore.
E così via.
