Un esempio di costruzione del diagramma di Bode

Per costruire un diagramma di Bode si parte da una funzione di trasferimento in forma fattorizzata con zeri al numeratore e poli al denominatore.

$$G(s) = \frac{(s-1) \cdot (s+10)}{s(s^2+s+16)}$$

Nota. Questa funzione non può essere ulteriormente fattorizzata. Il polinomio al denominatore ha il determinante negativo, quindi non ha radici e non può essere ulteriormente fattorizzato.

Il diagramma del modulo

Metto in evidenza i coefficienti -1 e +10 al numeratore per scorporarli.

$$G(s) = \frac{(-1) \cdot (1-s) \cdot (10) \cdot (\frac{s}{10}+1)}{s(s^2+s+16)}$$

$$G(s) = (-1) \cdot (10) \cdot \frac{ (1-s) \cdot (\frac{s}{10}+1)}{s(s^2+s+16)}$$

Ora metto in evidenza 16 al denominatore per scorporarlo.

$$G(s) = (-1) \cdot (10) \cdot \frac{ (1-s) \cdot (\frac{s}{10}+1)}{s \cdot 16 \cdot (\frac{s^2}{16}+\frac{s}{16}+1)}$$

$$G(s) = \frac{(-1) \cdot (10)}{16} \cdot \frac{ (1-s) \cdot (\frac{s}{10}+1)}{s \cdot (\frac{s^2}{16}+\frac{s}{16}+1)}$$

$$G(s) = \frac{-10}{16} \cdot \frac{ (1-s) \cdot (\frac{s}{10}+1)}{s \cdot (\frac{s^2}{16}+\frac{s}{16}+1)}$$

$$G(s) = \frac{-5}{8} \cdot \frac{ (1-s) \cdot (\frac{s}{10}+1)}{s \cdot (\frac{s^2}{16}+\frac{s}{16}+1)}$$

In questo modo ottengo il guadagno di Bode K=-5/8 che in decibel diventa.

$$| K |_{dB} = 20 \log | \frac{-5}{8} | = -4.08$$

Quindi il grafico della funzione passa circa a - 4 dB

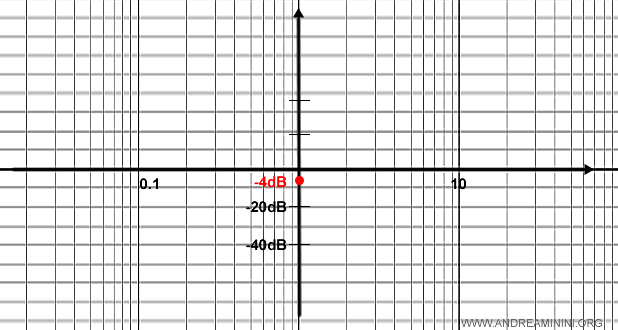
Ora scorporo il polo nell'origine ossia il fattore s al denominatore con molteplicità v=1.

$$G(s) = \frac{-5}{8} \cdot \frac{1}{s} \cdot \frac{ (1-s) \cdot (\frac{s}{10}+1)}{ \frac{s^2}{16}+\frac{s}{16}+1}$$

A questo punto sostituisco la s con jω e ottengo funzione nella forma di Bode.

$$G(jω) = \frac{-5}{8} \cdot \frac{1}{jω} \cdot \frac{ (1-jω) \cdot (\frac{jω}{10}+1)}{ \frac{(jω)^2}{16}+\frac{jω}{16}+1}$$

Con un semplice confronto con la funzione di Bode standard riconosco le varie componenti della funzione.

La funzione di Bode standard $$G(s) = K \cdot \frac{ \ (1+τ'_1s) \cdot (1+τ'_2s) \cdot \cdot \cdot ( 1 + \frac{2sδ'_1}{ω'_{n,1}} + \frac{s^2}{ω_{n,1}^{2'}} ) \cdot ( 1 + \frac{2sδ'_2}{ω'_{n,2}} + \frac{s^2}{ω_{n,2}^{2'}} ) \cdots }{ s^v \cdot (1+τ_1s) \cdot (1+τ_2s) \cdot \cdot \cdot ( 1 + \frac{2sδ_1}{ω_{n,1}} + \frac{s^2}{ω_{n,1}^2} ) \cdot ( 1 + \frac{2sδ_2}{ω_{n,2}} + \frac{s^2}{ω_{n,2}^2} ) \cdots }$$ ossia $$G(jω) = K \cdot \frac{ \ (1+τ'_1jω) \cdot (1+τ'_2jω) \cdot \cdot \cdot ( 1 + \frac{2jωδ'_1}{ω'_{n,1}} + \frac{(jω)^2}{ω_{n,1}^{2'}} ) \cdot ( 1 + \frac{2jωδ'_2}{ω'_{n,2}} + \frac{(jω)^2}{ω_{n,2}^{2'}} ) \cdots }{ (jω)^v \cdot (1+τ_1jω) \cdot (1+τ_2jω) \cdot \cdot \cdot ( 1 + \frac{2jωδ_1}{ω_{n,1}} + \frac{(jω)^2}{ω_{n,1}^2} ) \cdot ( 1 + \frac{2jωδ_2}{ω_{n,2}} + \frac{(jω)^2}{ω_{n,2}^2} ) \cdots }$$

Al numeratore ci sono costanti di tempo.

$$τ_1= -1 \\ τ_2 =-\frac{1}{10}=-0.1$$

Nota. Quindi ci sono due punti di rottura in corrispondenza di $$\frac{1}{|τ_1|} = \frac{1}{|-1|} = 1$$ $$\frac{1}{|τ_2|} = \frac{1}{|-0.1|} = 10$$

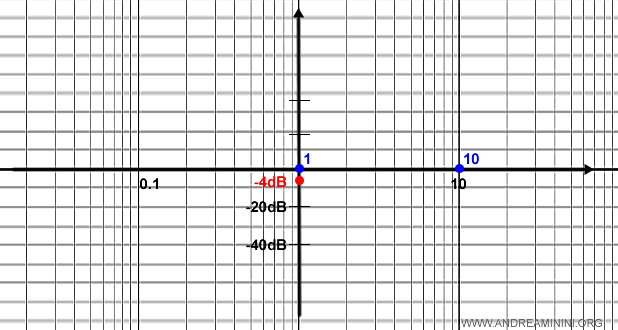
Al denominatore c'è, invece, una coppia di poli complessi e coniugati.

$$ω_{n,1}^2 = 16$$

Nota. Quindi la pulsazione naturale è $$ω_n = \sqrt{16} = 4$$ E' un altro punto di rottura del grafico

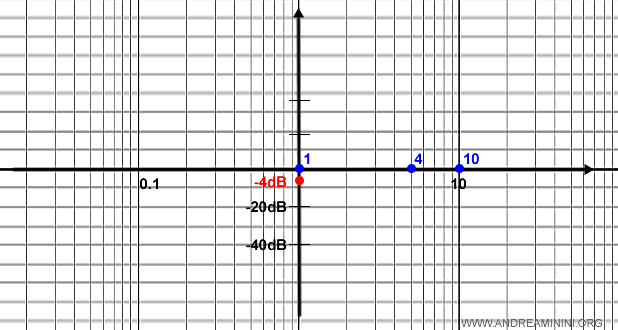
$$\frac{2δ_1}{ω_{n,1}} = \frac{1}{16}$$

Nota. Quindi il coefficiente di smorzamento è $$\frac{2δ_1}{4} = \frac{1}{16}$$ $$\frac{δ_1}{2} = \frac{1}{16}$$ $$δ_1 = \frac{2}{16}$$ $$δ_1 = \frac{1}{8} = 0.125$$ Essendo minore di 1/√2 c'è sicuramente un picco di risonanza.

Ora posso tracciare il grafico.

Il termine monomio è una retta con pendenza -20dB per decade ( -1 ) fino al primo punto di rottura.

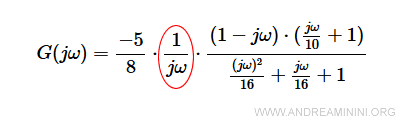
Spiegazione $$20 \log \frac{1}{jω} = 20 \log 1 - 20 \log jω = - 20 \log jω$$

La retta passa per il punto -4dB sull'asse delle ordinate.

Quindi individuo un altro punto della retta alle coordinate -4+20=16dB in una decade prima (0.1) e traccio la retta.

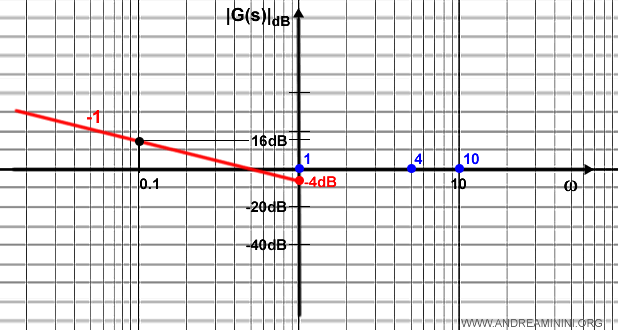
Nel primo punto di rottura a 1ω devo considerare il binomio (1-jω).

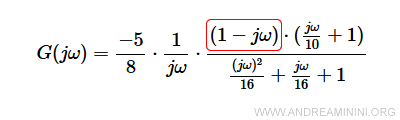
Si tratta di uno zero con pendenza 20dB per decade (+1).

Il segnale va sovrapposto al precedente (-1).

Quindi -1+1=0. Il segnale complessivo è costante (0) fino al secondo punto di rottura.

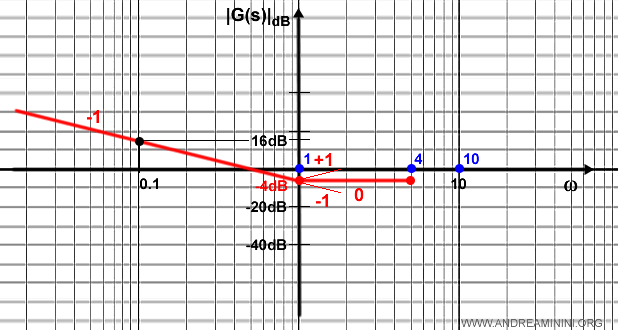
Nel secondo punto di rottura a 4ω devo considerare il trinomio.

Si tratta una nuova retta pendenza di -40dB per decade (-2) che si sovrappone alla precedente.

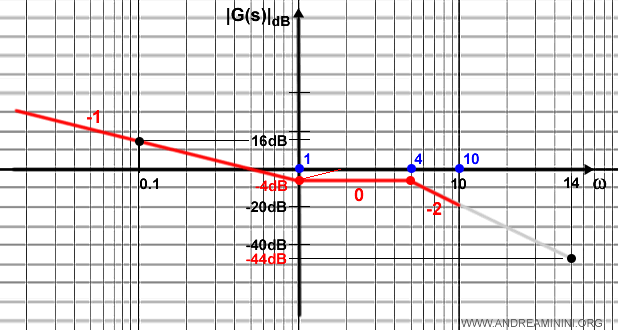
Nel terzo punto di rottura devo considerare un altro zero a 10ω.

E' una nuova retta pendenza di +20dB per decade (+1) che si sovrappone alla precedente (-2).

Quindi, a partire da 10w a curva modifica la pendenza a -1.

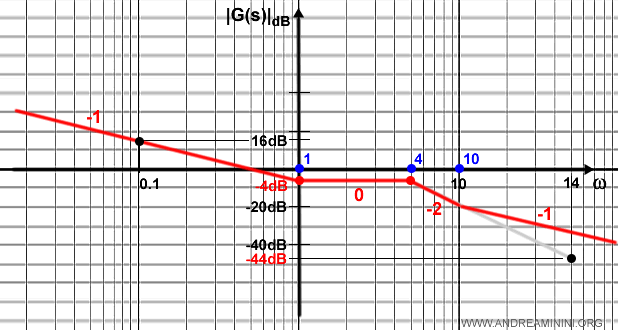
La rappresentazione del diagramma di Bode in forma asintotica termina qui.

Ovviamente, il grafico non è preciso e deve essere ancora corretto con lo studio del picco di risonanza e della frequenza di risonanza.

La formula della pulsazione di risonanza è

$$ω_r = ω_n \cdot \sqrt{ 1 - 2δ^2}$$

Sapendo che δ=0,125 e ω_n=4

$$ω_r = 4 \cdot \sqrt{ 1 - 2 \cdot (0,125^2 ) }$$

$$ω_r = 4 \cdot \sqrt{ 1 - 0,03 }$$

$$ω_r = 4 \cdot \sqrt{ 0,97 }$$

$$ω_r = 4 \cdot 0,984$$

$$ω_r ≅ 3,94$$

La formula del picco di risonanza è

$$|M_R|_{dB} = 20 \log ( \frac{1}{ 2δ \sqrt{ 1- δ^2 } } )$$

Sapendo che δ=0,125

$$|M_R|_{dB} = 20 \log ( \frac{1}{ 2·0,125 \sqrt{ 1- 0,125^2 } } )$$

$$|M_R|_{dB} = 20 \log ( \frac{1}{ 0,25 \sqrt{ 1- 0,02 } } )$$

$$|M_R|_{dB} = 20 \log ( \frac{1}{ 0,25 \sqrt{ 0,98 } } )$$

$$|M_R|_{dB} = 20 \log ( \frac{1}{ 0,25 \cdot 0,99 } )$$

$$|M_R|_{dB} = 20 \log 4$$

$$|M_R|_{dB} = 20 \cdot (0,602) ≅ 12 dB$$

Individuo sull'ascisse la pulsazione di risonanza ω_r=3,84 ω

In questa posizione il grafico si trova a -4dB sulle ordinate, salgo di +12dB e individuo il picco di risonanza.

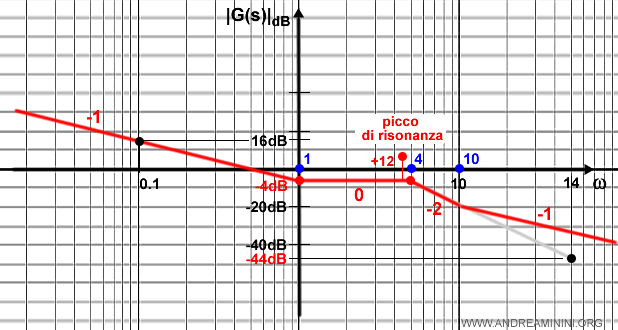
Inoltre, nell'origine c'è un errore di +3dB.

L'andamento corretto del grafico è il seguente:

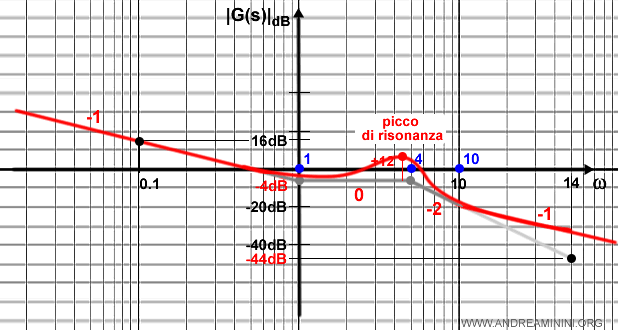
Nota. I punti di rottura sono tutti vicini entro una decada. Pertanto, le correzioni a un punto di rottura influenzano anche gli altri. In questo esercizio evito di considerare questi aspetti per semplicità. In realtà, tanto più i punti di rottura sono vicini tanto più si influenzano. Pertanto, andrebbero considerati. Se invece sono distanti più di una decade l'influenza è quasi nulla.

Una volta ultimato il diagramma del modulo, passo al diagramma della fase.

Il diagramma della fase

Riprendo la forma di Bode della funzione

$$G(jω) = \frac{-5}{8} \cdot \frac{1}{jω} \cdot \frac{ (1-jω) \cdot (\frac{jω}{10}+1)}{ \frac{(jω)^2}{16}+\frac{jω}{16}+1}$$

La costante K vale -5/8 ed è negativa. Quindi, c'è uno sfasamento di -180° nel tratto iniziale.

C'è anche un polo passante per l'origine con molteplicità h=-1. Quindi devo sottrarre altri -90°.

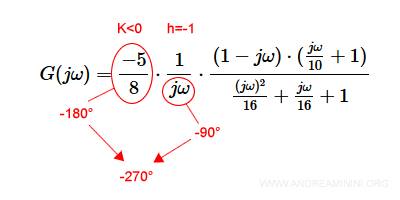
Complessivamente, la fase è uguale a -270° da 0 fino al primo punto di rottura.

Per semplicità comincio a disegnare il diagramma in forma asintotica.

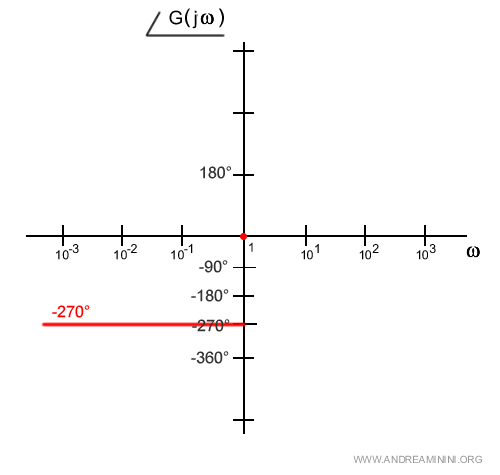
Il primo punto di rottura è uno zero (ω=1) del binomio (1-jω) con molteplicità h=1.

Il binomio causa una riduzione di ulteriori -90° della fase che scende a -360°.

La fase si mantiene a questo livello fino al successivo punto di rottura.

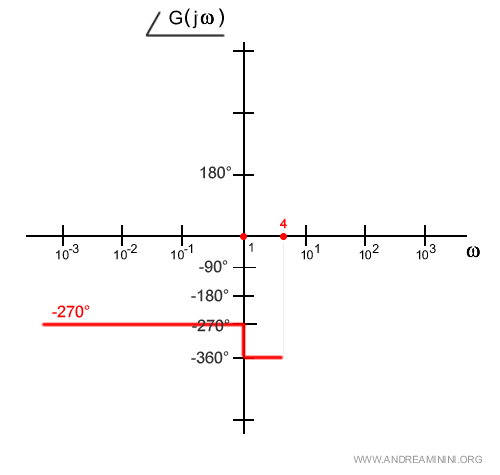
Il punto di rottura ω=4 (pulsazione naturale ω_n) è dovuto alla coppia di poli complessi e coniugati nel trinomio al denominatore (h=-1).

Essendo δ=0.125, ossia δ>0, nel punto di rottura ω=4 si verifica una riduzione di -180° della fase.

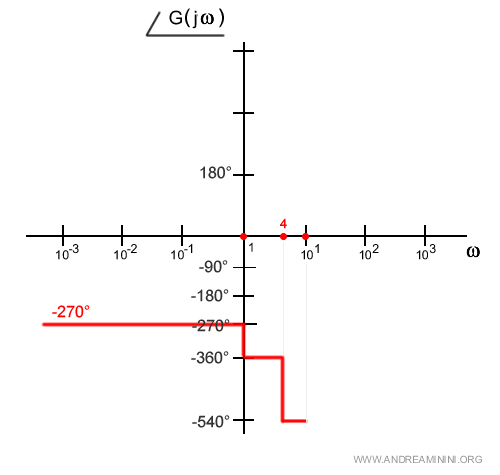
L'ultimo punto di rottura (ω=10) è relativo al secondo binomio al numeratore (h=1).

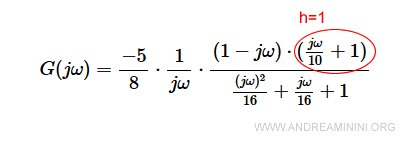
A partire da questo punto la fase sale di 90°.

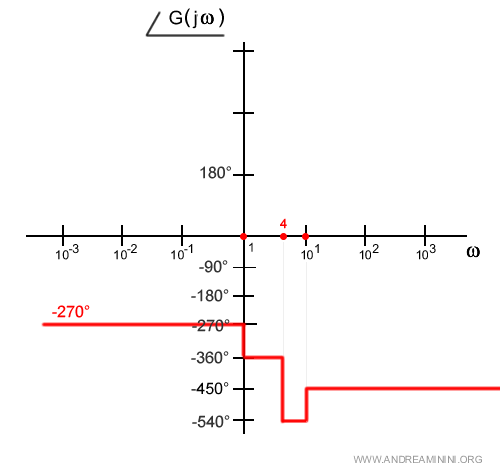
Non essendoci altri punti di rottura la fase resta costante a -450°.

Questo è il diagramma asintotico della fase.

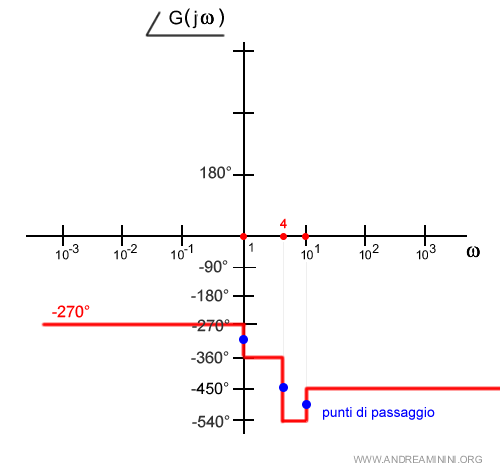
Per correggerlo, fisso i punti di passaggio della fase ( blu ).

Una decade prima di ogni punto di passaggio la fase comincia a modificare il proprio andamento.

Nota. Poiché i punti di passaggio sono molto vicini tra loro, entro una decade, si influenzano l'uno con l'altro. Per semplicità non considero questo aspetto.

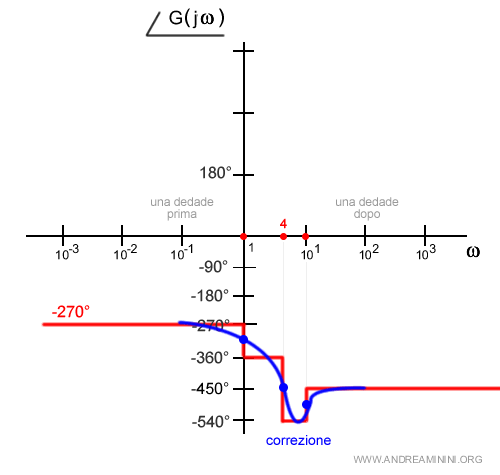
Congiungo i vari punti intermedi e ottengo una rappresentazione più precisa della fase.

Ecco il diagramma della fase corretto.

E così via.