Le rette parallele, coincidenti e incidenti

Due rette r₁ e r₂ nel piano possono essere

• Rette parallele. Se non hanno nessun punto in comune.
• Rette coincidenti. Se hanno tutti gli infiniti punti in comune.
• Rette incidenti. Se hanno un solo punto in comune.

Queste condizioni possono essere verificate facilmente sia con le equazioni parametriche che cartesiane.

Equazione parametriche della retta

Ho due rette r₁ e r₂

$$ \begin{cases} x=x_1+l_1t_1 \\ y = y_1+m_1t_1 \end{cases} $$

$$ \begin{cases} x=x_2+l_2t_2 \\ y = y_2+m_2t_2 \end{cases} $$

Per essere parallele, i loro vettori direttori devono essere linearmente dipendenti.

$$ v_1 = \begin{pmatrix} l_1 \\ m_1 \end{pmatrix} $$

$$ v_2 = \begin{pmatrix} l_2 \\ m_2 \end{pmatrix} $$

Esempio di vettori direttori

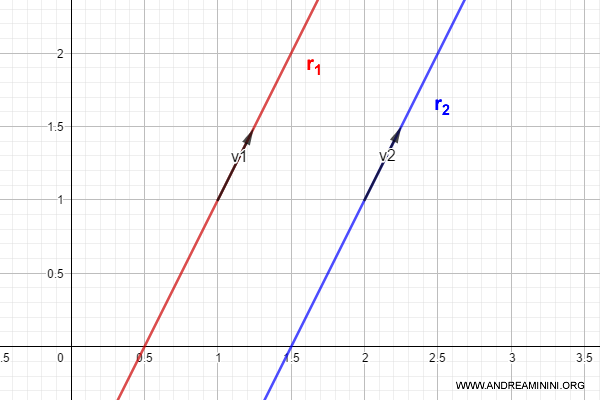
In questo caso, se linearmente dipendenti, il determinante della matrice composta dai due vettori è nullo.

$$ det \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \end{pmatrix} = 0 $$

Come capire se sono rette coincidenti?

Una volta appurato che sono rette parallele, per verificare se sono anche coincidenti, basta prendere un punto P qualsiasi della prima retta e verificare se appartiene anche alla seconda retta.

Come capire se sono rette incidenti?

Se i vettori non sono linearmente dipendenti, le due rette sono incidenti.

In questo caso il determinante della matrice dei vettori è diverso da zero.

$$ det \begin{pmatrix} l_1 & l_2 \\ m_1 & m_2 \end{pmatrix} \ne 0 $$

Esempio

Ho due rette

$$ \begin{cases} x=5+4t_1 \\ y = 2+2t_1 \end{cases} $$

$$ \begin{cases} x=3+4t_2 \\ y = 1+2t_2 \end{cases} $$

Il determinante della matrice dei vettori direttori è nullo.

$$ det \begin{pmatrix} 4 & 2 \\ 4 & 2 \end{pmatrix} = 0 $$

pertanto le due rette sono parallele.

Equazione cartesiane della retta

Ho due rette r₁ e r₂

$$ a_1 x + b_1 y + c_1 = 0 $$

$$ a_2 x + b_2 y + c_2 = 0 $$

In questo caso prendo come riferimento i vettori normali composti dai coefficienti.

$$ n_1 = \begin{pmatrix} a_1 \\ b_1 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} a_2 \\ b_2 \end{pmatrix} $$

I due vettori sono linearmente dipendenti se sono paralleli e il determinante è nullo.

$$ det \begin{pmatrix} a_1 & a_2 \\ b_1 & b_2 \end{pmatrix} = 0 $$

Se sono paralleli n₁ e n₂ allora anche le rette r₁ e r₂ sono parallele perché i vettori sono ortogonali alle rispettive rette.

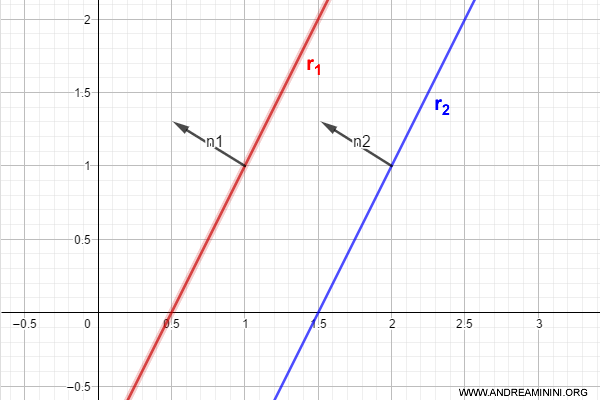
Devo però capire se sono rette parallele distinte o coincidenti.

Per farlo calcolo il rango della matrice dei coefficienti delle rette.

$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} $$

Se il rango rk è massimo allora le rette sono parallele distinte.

Viceversa, sono rette coincidenti.

E se il determinante non è nullo?

Se il determinante è diverso da zero, allora i due vettori non sono linearmente dipendenti e le rette sono incidenti.

$$ det \begin{pmatrix} a_1 & a_2 \\ b_1 & b_2 \end{pmatrix} \ne 0 $$

In questo caso il sistema composto dalle equazioni delle due rette ammette una soluzione.

$$ \begin{cases} a_1 x + b_1 y + c_1 = 0 \\ a_2 x + b_2 y + c_2 = 0 \end{cases} $$

E così via.

Esempio

Ho le equazioni cartesiane di due rette

$$ -4 x + 2 y + 2 = 0 $$

$$ -2 x + y + 3 = 0 $$

I vettori normali delle due rette sono

$$ n_1 = \begin{pmatrix} -4 \\ 2 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} -2 \\ 1 \end{pmatrix} $$

Il determinante della matrice dei vettori normali è nullo

$$ det \begin{pmatrix} -4 & 2 \\ -2 & 1 \end{pmatrix} = 0 $$

pertanto le rette sono parallele tra loro

Per capire se sono distinte o coincidenti calcolo il rango della matrice dei coefficienti

$$ r_k \begin{pmatrix} -4 & 2 & 2 \\ -2 & 1 & 3 \end{pmatrix} $$

Il rango è uguale a 2.

Quindi le rette sono parallele e distinte tra loro.

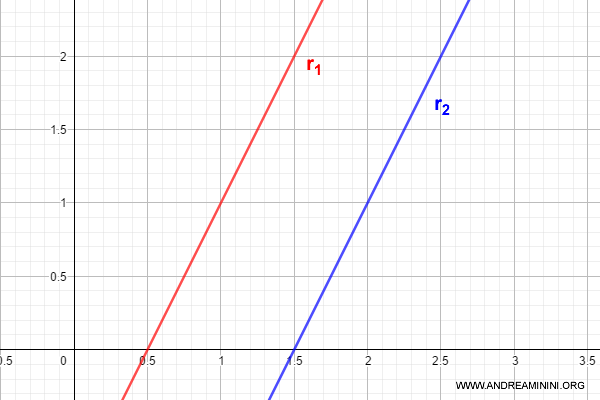
E così via.