La retta normale

La retta normale è una retta perpendicolare alla retta tangente in un punto P(x,y) della funzione f(x). $$ y-y_0=-\frac{1}{f'(x_0)} \cdot (x-x_0) $$

La retta normale e la retta tangente nel punto P formano quattro angoli di 90°.

Attenzione. La retta normale non può essere calcolata se f'(x₀)=0 ossia se la retta è parallela all'asse delle ascisse ( orizzontale ) in quanto il rapporto -1/f'(x₀) diventerebbe infinito ±∞ (indeterminato). E' l'unico caso in cui la formula non è applicabile. Tuttavia, il fatto che la retta normale non possa essere trovata con la precedente formula non vuol dire che una retta perpendicolare non esista in quel punto della funzione. Potrebbe esistere oppure no.

Come trovare la retta normale

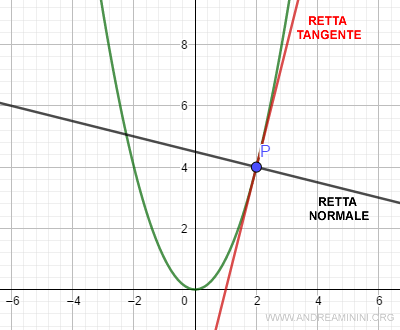
Prendo come esempio la funzione

$$ f(x) = x^2 $$

Nel punto x₀=2 la funzione f(x)=y₀=4.

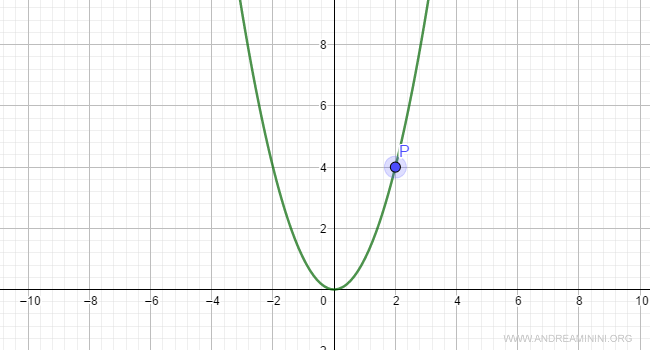
La retta tangente al punto x₀ ha per coefficiente angolare la derivata prima f'(x) della funzione nel punto x₀.

$$ f'(x) = 2x $$

$$ f'(x_0) = 2x_0 \:\:\: con \: x_0=2 $$

$$ f'(2) = 2 \cdot 2 = 4$$

L'equazione della retta tangente nel punto P(x₀,y₀) = P(2,4) è

$$ y-y_0 = f'(x_0) \cdot (x-x_0) $$

$$ y-4 = f'(x_0) \cdot (x-2) $$

$$ y = f'(x_0) \cdot (x-2) + 4 $$

Essendo f'(x₀)=4

$$ y = 4 \cdot (x-2) + 4 $$

$$ y =4x -4 $$

Ho così trovato la retta tangente nel punto P(x₀,y₀).

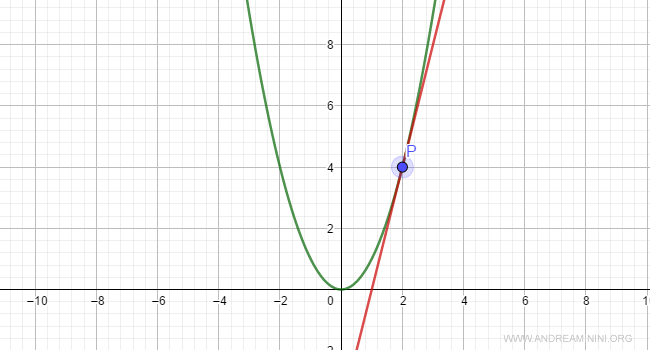
A questo punto, per trovare la retta normale nel punto P

$$ y-y_0=-\frac{1}{f'(x_0)} \cdot (x-x_0) $$

$$ y-4=-\frac{1}{4} \cdot (x-2) $$

$$ y=-\frac{x}{4} - \frac{2}{4} + 4 $$

$$ y=-\frac{x}{4} - \frac{1}{2} + 4 $$

$$ y=-\frac{x}{4} - \frac{1+8}{2} $$

$$ y=-\frac{x}{4} - \frac{9}{2} $$

Ho così trovato anche la retta normale nel punto P(x₀,y₀).

Dimostrazione

La retta normale e la retta tangente formano un angolo di 90°.

$$ a_1x_1 + b_1y_1 +c_1 = 0 $$

$$ a_2x_2 + b_2y_2 +c_2 = 0 $$

I vettori normali delle due rette sono:

$$ n_1 = \begin{pmatrix}a_1 \\ b_1 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix}a_2 \\ b_2 \end{pmatrix} $$

Essendo perpendicolari, i rispettivi vettori direttori e vettori normali delle rette sono vettori ortogonali e hanno un prodotto scalare uguale a zero.

$$ < n_1 , n_2 > = 0 $$

$$ < \begin{pmatrix}a_1 \\ b_1 \end{pmatrix} , \begin{pmatrix}a_2 \\ b_2 \end{pmatrix} > = a_1 a_2 + b_1 b_2 = 0 $$

In forma esplicita l'equazione della retta diventa.

$$ ax + by +c = 0 $$

$$ \frac{a}{b}x + \frac{b}{b}y +c = 0 $$

$$ \frac{a}{b}x + y +c = 0 $$

$$ y = -\frac{a}{b}x -c $$

$$ y = mx -c $$

Quindi

$$ y_1 = m_1 \cdot x_1 $$

$$ y_2 = m_2 \cdot x_2 $$

Dove m è il coefficiente angolare

$$ m = -\frac{a}{b} $$

Nella forma esplcita il vettore normale delle equazioni è

$$ n_1 = \begin{pmatrix} 1 \\ m_1 \end{pmatrix} $$

$$ n_2 = \begin{pmatrix} 1 \\ m_2 \end{pmatrix} $$

Pertanto il loro prodotto scalare

$$ < n_1 , n_2 > = 0 $$

$$ < \begin{pmatrix} 1 \\ m_1 \end{pmatrix} , \begin{pmatrix} 1 \\ m_2 \end{pmatrix} > = 1 \cdot 1 + m1 m_2 = 0 $$

$$ 1 + m1 m_2 = 0$$

$$ m1 m_2 = -1 0$$

Il coefficiente angolare della retta normale è -1 rispetto al coefficiente angolare della retta tangente.

Nota. Il coefficiente angolare della retta tangente è la derivata prima f'(x) della funzione nel punto x0.