Equazione cartesiana della retta
L'equazione cartesiana della retta può essere scritta in forma implicita o in forma esplicita.
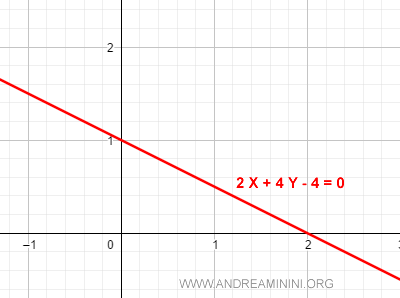
Equazione implicita della retta
$$ ax + by + c = 0 $$
E' la forma più difficile da interpretare geometricamente da una persona.
Inoltre, è composta da tre parametri (a,b,c).
Equazione esplicita della retta
$$ y = - \frac{a}{b}x - \frac{c}{b} $$
Quest'ultima forma equivale a una funzione lineare
$$ y = m x + n $$
dove
$$ m= - \frac{a}{b} $$
$$ n= - \frac{c}{b} $$
Il parametro m è detto coefficiente angolare della retta.
E' la pendenza della retta e forma un angolo θ tra l'asse delle ascisse e la retta.
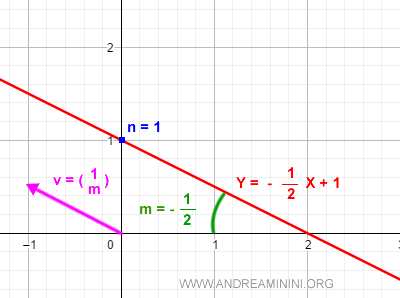
Il parametro m è uguale alla tangente goniometrica dell'angolo θ
$$ m = tan(θ) $$
Il parametro m determina anche il vettore direttore della retta.
$$ v = \begin{pmatrix} 1 \\ m \end{pmatrix} $$
Il parametro n è detto intercetta della retta.
E' il punto di intersezione con l'asse delle ordinate (asse y).
Nota. Quando il parametro c è nullo, la retta passa per l'origine O degli assi cartesiani.
L'equazione implicita della retta è unica.
Per ogni retta c'è una sola equazione implicita.
E' la forma più facile da interpretare ed è composta soltanto da due parametri (m,n) contro i tre parametri (a,b,c) della forma implicita.
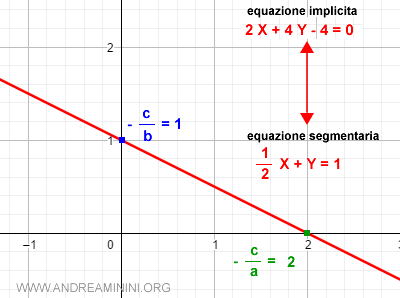
L'equazione segmentaria della retta
L'equazione segmentaria è un altro modo alternativo per rappresentare una retta.
$$ \frac{x}{p} + \frac{y}{q} = 1 $$
Dove
$$ p = - \frac{c}{a} $$
$$ q = - \frac{c}{b} $$
Il parametro p è il punto di intersezione della retta con l'ascisse (asse x).
Il parametro q è il punto di intersezione della retta con le ordinate (asse y).
Dimostrazione
$$ \frac{x}{- \frac{c}{a} } + \frac{y}{- \frac{c}{b}} = 1 $$
$$- \frac{a}{c} x + - \frac{b}{c} y = 1 $$
$$- a x + - b y = c $$
$$ a x + b y + c = 0 $$
