Come calcolare l'area di tre punti con il determinante dei vettori
Dati tre punti del piano P1,P2,P3 posso calcolare l'area del parallelogramma, costruito usando i tre punti come tre dei quattro vertici, tramite il valore assoluto del determinante dei vettori P1P2 e P1P3. $$ A = | det \begin{pmatrix} x_2-x_1 & x_3 - x_1 \\ y_2 - y_1 & y_3 - y_1 \end{pmatrix} | $$
Dividendo per due l'area del parallelogramma ottengo anche l'area del triangolo che ha per vertici i tre punti.
$$ A = \frac{1}{2} \cdot | det \begin{pmatrix} x_2-x_1 & x_3 - x_1 \\ y_2 - y_1 & y_3 - y_1 \end{pmatrix} | $$
Un esempio pratico
Ho tre punti sul piano cartesiano.
$$ P_1 \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$
$$ P_2 \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
$$ P_3 \begin{pmatrix} 5 \\ 4 \end{pmatrix} $$
Eccoli sul diagramma cartesiano
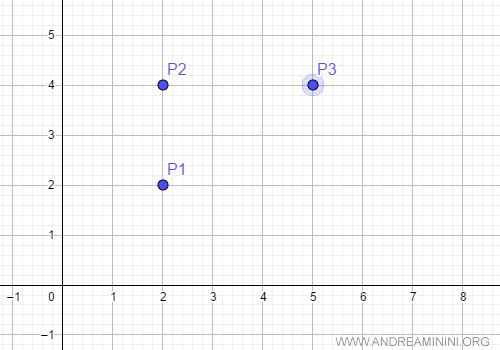
Per calcolare l'area del parallelogramma costruito sui tre punti, calcolo i vettori P1P2 e P1P3
$$ \overrightarrow{P_1P2 } = \begin{pmatrix} x_2-x_1 \\ y_2-y_1 \end{pmatrix} = \begin{pmatrix} 2-2 \\ 4-2 \end{pmatrix} = \begin{pmatrix} 0 \\ 2 \end{pmatrix} $$
$$ \overrightarrow{P_1P3} = \begin{pmatrix} x_3-x_1 \\ y_3-y_1 \end{pmatrix} = \begin{pmatrix} 5-2 \\ 4-2 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$
Ecco i vettori sul piano cartesiano.
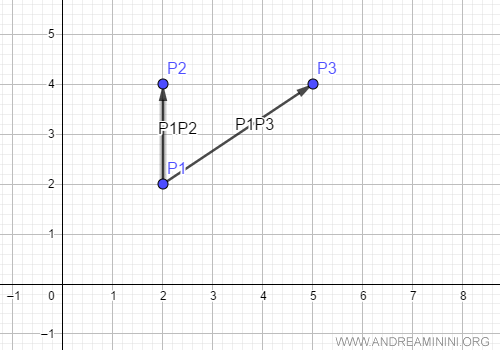
Poi calcolo il valore assoluto del determinante dei due vettori
I vettori sono posti in colonna dentro la matrice.
$$ A = | det \begin{pmatrix} 0 & 3 \\ 2 & 2 \end{pmatrix} | = | 0 \cdot 2 - 3 \cdot 2 | = | - 6 | = 6 $$
L'area del parallelogramma è uguale a 6.
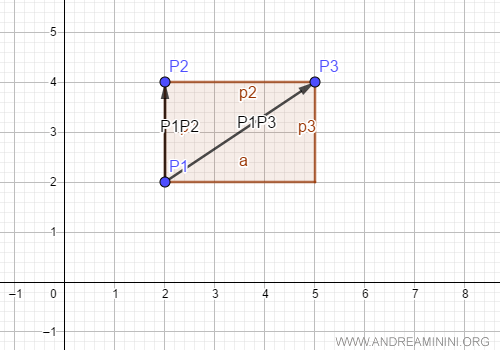
Per calcolare l'area del triangolo che ha per vertici i tre punti del piano, mi basta dividere per due l'area del parallelogramma.
$$ A' = \frac{A}{2} = \frac{6}{2} = 3 $$
Ho così ottenuto l'area della superficie tracciata dai tre punti sul piano cartesiano.
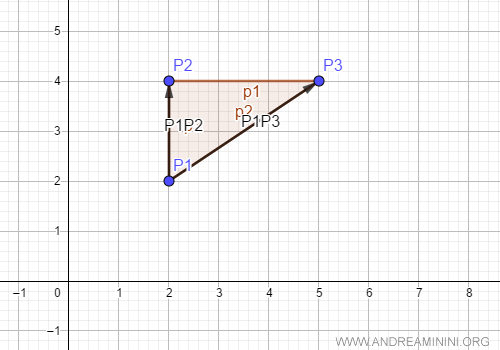
E' molto semplice.
E così via.
