L'interazione debole

L’interazione debole è una delle interazioni fondamentali della fisica della fisica, insieme all’interazione forte, a quella elettromagnetica e a quella gravitazionale. Agisce sia sui leptoni (come elettroni e neutrini) sia sui quark, e si manifesta tramite lo scambio di bosoni mediatori: $W^+$, $W^-$ e $Z^0$. Spesso è chiamata carica debole.

È l’unica forza capace di modificare il sapore delle particelle elementari, trasformando un quark o un leptone in un altro della stessa famiglia.

Per questo motivo è responsabile di processi come il decadimento beta nei nuclei instabili. Inoltre, poiché i neutrini vengono prodotti e rivelati attraverso interazioni deboli nei loro stati di sapore, questa forza è indirettamente coinvolta anche nel fenomeno delle oscillazioni dei neutrini.

Ha un raggio d’azione estremamente breve (circa $10^{-18}$ m) ed è molto meno intensa dell’interazione forte e di quella elettromagnetica. A basse energie la sua intensità effettiva può risultare fino a $10^11$ volte inferiore a quella elettromagnetica.

Va comunque precisato che i valori riportati per l’intensità delle interazioni sono soltanto ordini di grandezza indicativi a basse energie; in realtà le costanti di accoppiamento variano con l’energia del processo considerato. In generale, l’interazione debole ha un’intensità compresa tra circa $10^{5}$ e $10^{13}$ volte inferiore a quella della forza forte.

Nota. Pur essendo molto più debole, l’interazione debole svolge un ruolo fondamentale sia nella fisica delle particelle sia nei processi astrofisici, ad esempio nelle reazioni nucleari che alimentano le stelle.

Il decadimento beta e l'interazione debole

L’interazione debole è alla base del decadimento radioattivo beta, un processo attraverso il quale un nucleo atomico instabile può trasformarsi in uno più stabile. 

Un nucleo può essere instabile quando presenta un rapporto neutroni/protoni squilibrato.

Il decadimento beta consente al nucleo di riequilibrarsi trasformando un neutrone in protone o viceversa. Si tratta di una delle principali forme di radioattività naturale, accanto ai decadimenti alfa e gamma.

• Decadimento β⁻
  Un neutrone si trasforma in protone, con l’emissione di un elettrone e di un antineutrino elettronico:
   $$ n \;\;\to\;\; p + e^- + \bar{\nu}_e $$ A livello di quark, un quark down diventa un quark up tramite l’emissione di un bosone \$W^-\$ virtuale, che decade subito in \$e^-\$ e \$\bar{\nu}\_e\$.
  
• Decadimento β⁺
  Un protone si trasforma in neutrone, con l’emissione di un positrone e di un neutrino elettronico: $$p \;\;\to\;\; n + e^+ + \nu_e$$ Qui un quark up diventa down tramite l’emissione di un bosone \$W^+\$ virtuale, che decade in \$e^+\$ e \$\nu\_e\$.
  

  

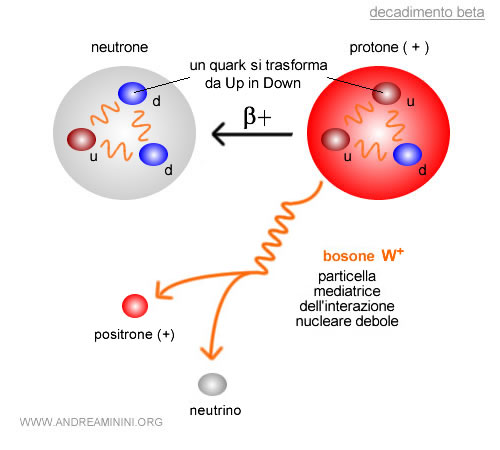
Questo meccanismo permette al nucleo di modificare il proprio rapporto tra protoni e neutroni, avvicinandosi a una configurazione energeticamente più stabile.

Il decadimento beta, oltre a essere una delle cause della radioattività naturale, riveste un ruolo fondamentale nelle reazioni nucleari che alimentano le stelle, come quelle che avvengono nel Sole.

Tipi di interazioni deboli (neutre o cariche)

Esistono due tipi di interazioni deboli.

• interazioni deboli neutre (NC, Neutral Current)
  Sono mediate dai bosoni $ Z $. In questo caso il fermione che entra al vertice è lo stesso che esce: non vi è cambiamento di flavour, analogamente a quanto accade per le interazioni elettromagnetiche e forti. Tuttavia, la loro caratteristica distintiva è la violazione della parità, che le rende riconoscibili anche quando “contaminano” processi dominati dall’elettromagnetismo, come in alcuni esperimenti di fisica atomica.

  Nota. Le interazioni deboli cariche erano note già dagli anni ’30, grazie agli studi di Fermi sul decadimento beta. Le interazioni deboli neutre furono invece previste teoricamente più tardi, alla fine degli anni ’60, da Glashow, Weinberg e Salam nell’ambito del modello elettrodebole (GWS). La loro previsione fu confermata sperimentalmente al CERN nel 1973, segnando una svolta storica: fino ad allora si conoscevano solo i processi mediati dai bosoni $W$, non quelli mediati dal $Z$.  Fu una svolta storica: fino ad allora si conoscevano solo i processi con $ W $, ma non con $ Z $.

• Interazioni deboli cariche (CC, Charged Current)
  Sono mediate dai bosoni $ W $. A differenza di tutte le altre interazioni fondamentali, hanno la capacità di cambiare il flavour (sapore) delle particelle. Ad esempio, un quark up può trasformarsi in un quark down, oppure un elettrone in un neutrino elettronico. Per questo motivo le interazioni deboli cariche sono responsabili dei veri processi di decadimento, come il decadimento beta nei nuclei.

  Nota. Nell’interazione forte i quark possono cambiare colore (es. da rosso a verde) ma non sapore; nell’interazione elettromagnetica i fermioni (quark e leptoni) possono emettere o assorbire fotoni senza cambiare né sapore né carica. Lo stesso accade nell’interazione debole neutra (NC), mediata dal bosone $Z$. Viceversa, nell’interazione debole carica (CC), mediata dal bosone $W^\pm$, una particella può cambiare sapore: ad esempio, un quark up può diventare un quark down, permettendo la trasformazione di un protone in un neutrone, o viceversa.

Prima di passare agli esempi, in questa tabella ho riepilogato le principali differenze tra le interazioni deboli neutre e cariche. In modo da ricordarle meglio a colpo d'occhio.

Tipo di interazione	Mediatore	Cambiamento di flavour (sapore)	Caratteristica distintiva
Debole neutra (NC)	Bosone Z0	No	Viola la parità, ma conserva carica e identità della particella
Debole carica (CC)	Bosoni W±	Sì	Responsabile dei decadimenti, trasforma un fermione in un altro

Esempi pratici

Alcuni esempi tipici di interazioni deboli sono lo scattering neutrino-elettrone $ \nu_{\mu} + e^- \to \nu_{\mu} + e^- $ e lo scattering neutrino-protone $ \nu_{\mu} + p \to \nu_{\mu} + p $.

Scattering neutrino-elettrone

Lo scattering neutrino - elettrone è un processo in cui un neutrino ($\nu$) urta contro un elettrone ($e^-$) e lo devia, trasferendogli parte della sua energia e quantità di moto: $$ \nu + e^- \;\to\; \nu + e^- $$ È un’interazione molto rara perché i neutrini non hanno carica elettrica, quindi non subiscono interazioni elettromagnetiche. L’unico canale possibile è tramite l’interazione debole.

Lo scattering può avvenire in due modi distinti:

• Scattering neutro (mediatore $Z^0$)
  Avviene per tutti i tipi di neutrini ($\nu_e, \nu_\mu, \nu_\tau$).  Il neutrino entra, scambia un bosone $Z^0$ virtuale con l’elettrone, ed esce sempre come neutrino dello stesso tipo: $$ \nu_\mu + e^- \;\to\; \nu_\mu + e^-  $$ Cambiano solo energia e direzione (urto elastico).
  
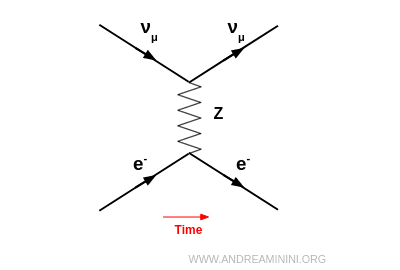
• Scattering carico (mediatore $W^\pm$)
  Qui il neutrino elettronico $\nu_e$ si trasforma in elettrone scambiando un $W$ con l’elettrone iniziale, che a sua volta diventa un neutrino elettronico: $$ \nu_e + e^- \;\to\; e^- + \nu_e  $$ In pratica, il neutrino e l’elettrone si “scambiano di ruolo”. In questo caso il risultato finale è lo stesso di uno scattering neutro ma è mediato da $ W $ (scattering carico) anziché da $ Z $.

Nota. Lo scattering neutrino - elettrone fu uno dei primi processi usati per confermare l’esistenza delle interazioni deboli neutre al CERN nel 1973. È un processo “pulito” perché non coinvolge nucleoni né interazioni forti, quindi permette di testare direttamente la teoria elettrodebole.

Scattering neutrino - protone

Lo scattering neutrino-protone è un urto in cui un neutrino interagisce con un protone.

Poiché i neutrini non hanno carica elettrica e non partecipano alle interazioni forti, l’unico canale possibile è l’interazione debole mediata da bosoni $W^\pm$ o $Z^0$.

Ci sono due grandi famiglie, analoghe al caso neutrino - elettrone:

• Scattering debole neutro (NC, neutral current)
  E' mediato dal bosone $Z^0$.  Il neutrino rimane dello stesso tipo e il protone rimane protone. Cambiano solo energia e direzione (urto elastico). Ad esempio, un neutrino muonico si scontra con un protone. $$ \nu_\mu + p \;\to\; \nu_\mu + p $$ Questo è stato il processo chiave per confermare nel 1973 al CERN l’esistenza delle correnti neutre.
  
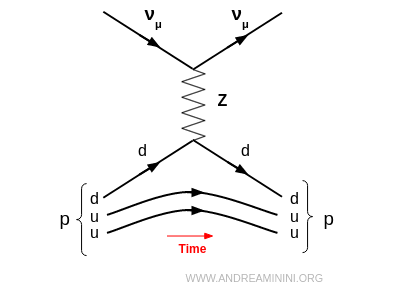
• Scattering debole carico (CC, charged current)
  E' mediato dal bosone $W^\pm$.  Il neutrino si trasforma in una particella carica (leptone) e il protone si trasforma in un altro nucleone (protone ↔ neutrone). Ad esempio, un neutrino elettronico interagisce con il protone, produce un positrone e trasforma il protone in un neutrone. $$ \nu_e + p \;\to\; e^+ + n $$ Questo è in pratica il processo inverso del decadimento beta. 

Entrambi sono processi rarissimi, per osservarli servono rivelatori molto grandi e fasci intensi di neutrini.

L'interazione debole tra leptoni

L’interazione debole carica tra leptoni, mediata dai bosoni $W^\pm$, consente la trasformazione reciproca tra un neutrino (carica $0$) e il suo leptone carico associato (carica $-e$), ma solo all’interno della stessa generazione.

In generale l'interazione debole può agire su tutti i leptoni (elettrone, muone, tauone, e rispettivi neutrini).

Nello scattering neutro ( mediatore $ Z^0 $ ) due leptoni interagiscono scambiando un bosone $Z^0$.

In questo caso le particelle coinvolte rimangono le stesse (nessun cambiamento di flavour), ma possono modificare la propria energia e direzione.

Ad esempio, un neutrino muonico può diffondere su un elettrone tramite lo scambio di un bosone $Z^0$: $$
\nu_\mu + e^- \;\to\; \nu_\mu + e^- $$ In questo processo sia il neutrino sia l’elettrone rimangono della stessa specie, ma cambiano energia e direzione.

Nello scattering carico (mediatore $W $), invece, un leptone carico e il neutrino della stessa generazione si trasformano l’uno nell’altro (es. $ e^- \leftrightarrow \nu_e $ , $ e^+ \leftrightarrow \bar{\nu}_e $ ) tramite lo scambio di un bosone $W$.

$$ l^- \leftrightarrow \nu_l + W^- $$

Quindi, nelle interazioni deboli i leptoni si trasformano sempre all’interno della propria famiglia.

• L’elettrone $(e^-)$ è accoppiato solo al suo neutrino elettronico $(\nu_e)$
• Il muone $(\mu^-)$ solo al neutrino muonico $(\nu_\mu)$
• Il tau $(\tau^-)$ solo al neutrino tauonico $(\nu_\tau)$.

In altre parole, in un singolo vertice del diagramma di Feynman il numero leptonico deve essere sempre conservato

Spiegazione. Nell’interazione debole, ogni leptone carico è accoppiato solo al suo neutrino di generazione attraverso il bosone $W$. Questo implica che, in un vertice debole del diagramma di Feynman, il numero leptonico elettronico $L_e$, muonico $L_\mu$ e tauonico $L_\tau$ restano invariati separatamente: ad esempio $e^- \leftrightarrow \nu_e$, $\mu^- \leftrightarrow \nu_\mu$. Perciò un elettrone non può trasformarsi in un neutrino muonico, né un muone in un neutrino elettronico. In altre parole, l’interazione debole conserva il numero leptonico per ciascuna famiglia.

L’interazione può essere descritta sia come emissione sia come assorbimento di un $ W $.

Emissione di un bosone W

Ogni leptone carico può emettere un bosone $ W $.

• Un leptone carico negativamente ($e^-$, $\mu^-$, $\tau^-$) può trasformarsi nel proprio neutrino emettendo un $W^-$.   $$ \ell^- \;\to\; \nu_\ell + W^-    $$
• Un leptone carico positivamente ($e^+$, $\mu^+$, $\tau^+$) fa l’opposto: può trasformarsi nell’antineutrino corrispondente emettendo un $W^+$.  $$ \ell^+ \;\to\; \bar{\nu}_\ell + W^+  $$

Quindi, le particelle negative emettono $W^-$, le antiparticelle positive emettono $W^+$.

Ad esempio, un muone negativo $\mu^-$ può trasformarsi in un neutrino muonico $\nu_\mu$ emettendo un $W^-$, che a sua volta viene assorbito da un neutrino elettronico $\nu_e$ producendo un elettrone $e^-$: $$ \mu^- + \nu_e \;\to\; \nu_\mu + e^- $$

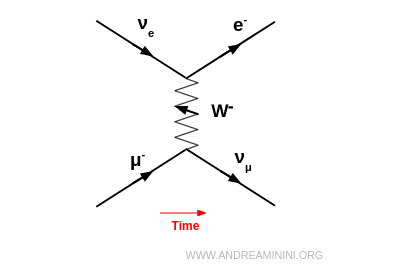
Se invece il bosone $W^-$ non viene assorbito, esso può decadere in un elettrone e un antineutrino elettronico: $$ W^- \;\to\; e^- + \bar{\nu}_e $$ In questo caso, il processo complessivo è il decadimento del muone. $$ \mu^- \;\to\; \nu_\mu + e^- + \bar{\nu}_e $$

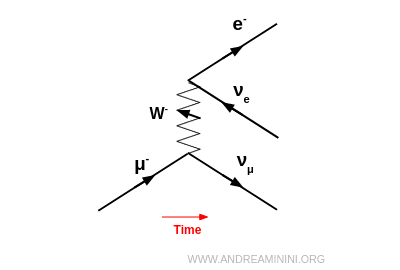
Assorbimento di un bosone W

D'altra parte, ogni leptone può anche assorbire $ W $, trasformandosi nella particella (o antiparticella) associata:

• Un neutrino può assorbire un $W^-$ trasformandosi nel corrispondente leptone carico negativo:  $$  \nu_\ell + W^- \;\to\; \ell^-   $$
• Un antineutrino può assorbire un $W^+$ trasformandosi nel corrispondente leptone carico positivo: $$
    \bar{\nu}_\ell + W^+ \;\to\; \ell^+ $$

Ad esempio, un positrone ($e^+$) si trasforma nel proprio antineutrino elettronico $\bar{\nu}_e$ emettendo un $W^+$; lo stesso $W^+$ viene assorbito da un antineutrino muonico $\bar{\nu}_\mu$, che si trasforma in un muone positivo $\mu^+$. Il processo complessivo è: $$ e^+ + \bar{\nu}_\mu \;\to\; \bar{\nu}_e + \mu^+ $$

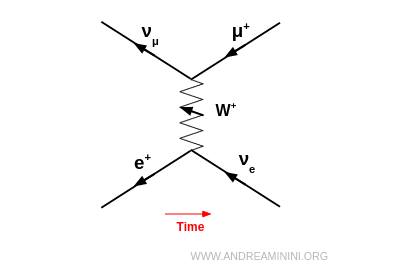
Trattandosi di antiparticelle, nel diagramma di Feynman hanno la freccia nel verso opposto rispetto al tempo. Il diagramma va però letto sempre da sinistra verso destra seguendo la freccia del tempo.

L'interazione debole tra quark

L’interazione debole carica tra quark, mediata dai bosoni $W^\pm$, consente la trasformazione reciproca tra un quark con carica $+\tfrac{2}{3}e$ e un quark con carica $-\tfrac{1}{3}e$, anche appartenenti a generazioni diverse, con probabilità fissate dagli elementi della matrice CKM.

Ad esempio, i quark con carica $-\tfrac{1}{3}$ (quark down $d$, strange $s$, bottom $b$) possono trasformarsi in un quark con carica $+\tfrac{2}{3}$ (quark up $u$, charm $c$, top $t$), emettendo un bosone $W^-$.

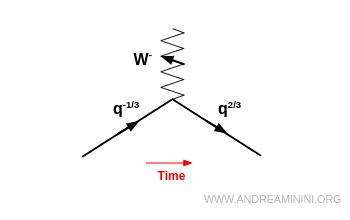
In questa trasformazione il quark conserva il numero barionico ma cambia flavour (sapore).

Nota. Va specificato che il bosone $ W^- $ non porta via il flavour. Semplicemente, è il quark stesso che cambia sapore nella transizione.

Il bosone $W$ emesso può:

• decadere spontaneamente in una coppia leptone + antineutrino ($e^- + \bar\nu_e$, $\mu^- + \bar\nu_\mu$, ecc.).
  

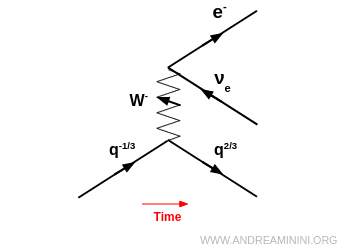
  Nota. Ad esempio, è quello che che accade nel decadimento beta $ β^- $ quando un neutrone decade in un protone $ n \to p +e^- + \bar{\nu}_e $
  

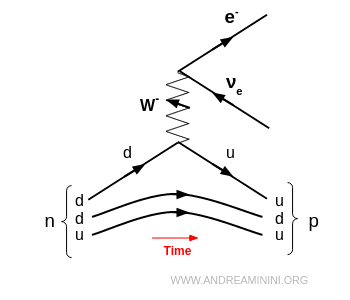
• essere assorbito da un neutrino, che si trasforma nel corrispondente leptone carico ( es. $ \nu_e \to e^- $ ) dando luogo a un processo semileptonico (es. $ d + \nu_e \to u + e^- $)
  
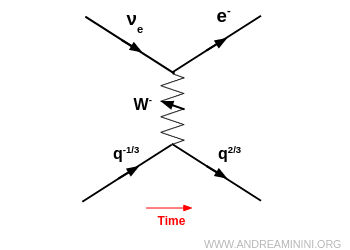
• essere assorbito da un quark, dando luogo a una trasformazione di sapore in un altro vertice debole (processo puramente adronico).

  Ad esempio, la particella $ \Lambda $ è un barione, una particella composta da tre quark (up, down, strange), appartenente alla famiglia degli iperoni che decade in un protone e in un pione $ \Lambda \to p + \pi^- $ convertendo un quark strange (s) in un quark up (u).
  
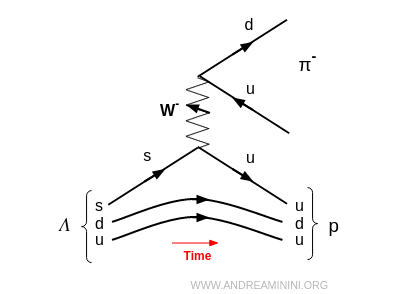
  Quest'ultimo esempio mostra però un problema, un quark strange (s) si trasforma in up (u), si verifica uno scambio tra quark di generazioni diverse.

I fisici inizialmente si aspettavano che anche i quark, come i leptoni, seguissero la regola dei vertici deboli confinati alla stessa generazione, ma scoprirono con sorpresa che i quark possono cambiare sapore anche tra generazioni diverse.

Nel 1963 Nicola Cabibbo propose l’idea che i quark di tipo down ($d, s$) non partecipassero ai vertici deboli come stati “puri”, ma come una loro combinazione lineare, introducendo l’angolo di mescolamento (angolo di Cabibbo) per spiegare i decadimenti con cambiamento di stranezza.

Circa dieci anni dopo, nel 1973, Makoto Kobayashi e Toshihide Maskawa estesero questa idea a tre generazioni di quark.

Questo portò alla formulazione della matrice CKM (Cabibbo-Kobayashi-Maskawa), che descrive il mescolamento tra diverse generazioni di quark nell’interazione debole come una combinazione lineare degli stati di tipo down ($d,s,b$).

In pratica, il quark down $ d $ non si accoppia solo con il quark $ u $ ma una combinazione di $d, s, b$. Lo stesso vale per $c$ e $t$.

$$ (u,d'),\quad (c,s'),\quad (t,b') $$

Dove $d', s', b'$ sono “quark misti”, cioè combinazioni lineari di $d, s, b$.

$$ d' = V_{ud}\, d + V_{us}\, s + V_{ub}\, b $$

$$ s' = V_{cd}\, d + V_{cs}\, s + V_{cb}\, b $$

$$ b' = V_{td}\, d + V_{ts}\, s + V_{tb}\, b $$

Dove $V_{ud}$ mi dice quanto il quark $d$ contribuisce a formare $d'$, $V_{us}$ quanto il quark $s$ contribuisce a formare $d'$ e così via…

Scrivendo le relazioni in forma compatta, le combinazioni lineari dei quark $d', s', b'$ possono essere espresse come un prodotto vettore-matrice.

$$
\begin{pmatrix} d' \\ s' \\ b' \end{pmatrix}
=
\begin{pmatrix}
V_{ud} & V_{us} & V_{ub} \\
V_{cd} & V_{cs} & V_{cb} \\
V_{td} & V_{ts} & V_{tb}
\end{pmatrix}
\begin{pmatrix} d \\ s \\ b \end{pmatrix}
$$

La matrice dei coefficienti $V_{ij}$ prende il nome di matrice CKM (Cabibbo - Kobayashi - Maskawa).

Se questa matrice fosse esattamente una matrice identità, ci sarebbe semplicemente tre accoppiamenti $d'=d$, $s'=s$, $b'=b$.

In realtà non è così: anche se la matrice CKM tende ad assomigliare a una matrice identità, non lo è.

Di conseguenza, i quark possono cambiare flavour non solo all’interno della stessa generazione, ma anche tra generazioni diverse, quando interagiscono tramite la forza debole.

Nota. Senza questo meccanismo, il quark $u$ potrebbe trasformarsi solo in $d$ e viceversa. Invece, grazie a $V_{us} \neq 0$, può trasformarsi anche in strange $s$.  Questo spiega i processi che cambiano la stranezza.

In altre parole, la matrice CKM spiega come i quark di tipo “up” ($u, c, t$) si possono trasformare in quark di tipo “down” ($d, s, b$) con certe probabilità.

I valori sperimentali della tabella CKM (al 2020) indicano quali sono queste ampiezze di probabilità.

$$ \begin{bmatrix} |V_{ud}| & |V_{us}| & |V_{ub}| \\ |V_{cd}| & |V_{cs}| & |V_{cb}| \\ |V_{td}| & |V_{ts}| & |V_{tb}| \end{bmatrix} = \begin{bmatrix} 0.97370 \pm 0.00014 & 0.2245 \pm 0.0008 & 0.00382 \pm 0.00024 \\ 0.221 \pm 0.004 & 0.987 \pm 0.011 & 0.0410 \pm 0.0014 \\ 0.0080 \pm 0.0003 & 0.0388 \pm 0.0011 & 1.013 \pm 0.030 \end{bmatrix} $$

Ad esempio, dalla prima riga della matrice si osserva che il quark up ( $ u $) può accoppiarsi con un quark down ( $ d $) con ampiezza di probabilità pari a circa 97%,  un quark strange ( $s $) con ampiezza del 22%,  un quark bottom ($ b $) con ampiezza dello 0,4%.

Nota. La somma $97% + 22% + 0,4% $ risulta superiore al 100% perché non si tratta di probabilità, ma di ampiezze. Le probabilità reali si ottengono elevando al quadrato ciascun coefficiente: $$ |V_{ud}|^2 + |V_{us}|^2 + |V_{ub}|^2 = 1 $$ Quindi, nell'esempio precedente le probabilità sono: $$ |V_{ud}|^2 \approx (0.974)^2 \approx 0.949 $$ $$  |V_{us}|^2 \approx (0.225)^2 \approx 0.051 $$ $$  |V_{ub}|^2 \approx (0.0038)^2 \approx 0.000014 $$ La somma torna quindi esattamente al 100%: $$ 0.949 + 0.051 + 0.000014 \approx 1.000. $$

Questi numeri mi dicono quali decadimenti deboli sono favoriti e quali sono rari:

• $u \to d$ è la transizione più probabile, infatti i protoni e neutroni dominano la materia ordinaria.
• $s \to u$ è possibile ma meno probabile, ed è alla base dei decadimenti strani ($\Lambda, \Sigma, \Omega$).
• $t \to b$ è praticamente certo: per questo il quark top, quando decade, produce quasi sempre un quark bottom.

Quindi un $u$ può emettere un $W^+$ e diventare un $d$, ma anche (con probabilità minore) un $s$ o un $b$.

Nota. Nei leptoni il vertice debole collega sempre particelle della stessa generazione, a garanzia della conservazione dei numeri leptonici. L’eventuale mescolamento tra generazioni non avviene direttamente al vertice, ma solo in un secondo momento, attraverso il fenomeno delle oscillazioni dei neutrini. Nei quark, invece, il mescolamento tra famiglie è già incorporato nel vertice debole carico, ed è descritto dalla matrice CKM. In questo caso, dunque, il principio rimane lo stesso ( il bosone W media la transizione tra partner “up” e “down”) ma la corrispondenza non è più perfettamente ristretta a una sola generazione: l’interazione debole consente transizioni miscelate tra stati di quark appartenenti a generazioni diverse.

Note

Alcune note e osservazioni personali a margine sull'interazione debole

• Tracce dell’interazione debole neutra nei processi elettromagnetici
  In ogni scattering mediato da fotoni (interazione elettromagnetica), in linea di principio esiste anche un diagramma di Feynman analogo mediato dal bosone $Z^0$ (interazione debole neutra). L’ampiezza dovuta al $Z$ è però molto più piccola di quella fotonica alle energie ordinarie, quindi l’effetto è praticamente impercettibile a basse energie che lo si può ignorare. Solo a energie molto elevate (paragonabili alla massa del bosone $Z^0$, circa $91$ GeV) il contributo del $Z$ diventa non trascurabile e può essere rivelato sperimentalmente.
  

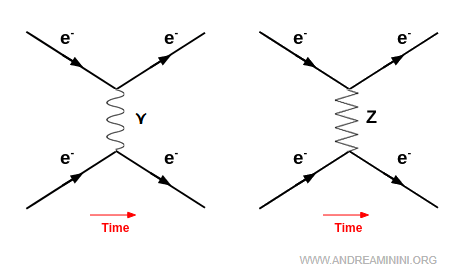
  Nota. Un esempio storico è fornito dagli esperimenti di scattering elettrone-positrone ad alta energia ($e^- + e^+ \to \mu^- + \mu^+$) condotti al DESY (Deutsches Elektronen-Synchrotron) di Amburgo negli anni ’70-’80, nei quali fu possibile osservare la correzione dovuta allo scambio del bosone neutro. Questo fenomeno rappresenta una traccia sperimentale dell’interazione debole anche nei processi elettromagnetici: un piccolo termine correttivo alla legge di Coulomb, che però diventa impercettibile a basse energie. Per osservare una neutral current priva di sovrapposizioni con l’elettromagnetismo, l’unica via pulita è lo scattering di neutrini, poiché i neutrini non hanno carica elettrica e quindi non interagiscono tramite fotoni. Tuttavia, questi esperimenti risultano particolarmente complessi a causa della bassissima sezione d’urto dei neutrini.

E così via.