Come fare un circuito logico dalla tavola di verità

Per disegnare un circuito logico occorre avere la tavola di verità e conoscere le regole dell'algebra booleana.

Esempio pratico

Ho la seguente tabella di verità e devo costruire il circuito logico.

Si tratta di un circuito con 3 valori in ingresso (x₁,x₂,x₃) e un valore in uscita y.

Come si costruisce il circuito logico?

Prendo come riferimento le combinazioni della tavola di verità che determinano un'uscita pari a 1 ( o vero ).

Ogni combinazione è una relazione AND (*) tra le tre variabili.

Quindi posso riscriverle in forma algebrica, negando le variabili quando sono uguali a zero.

Tutte queste combinazioni di valori generano un'uscita uguale a 1.

Quindi sono in relazione OR (+) tra loro e posso riscriverle sotto forma di espressione.

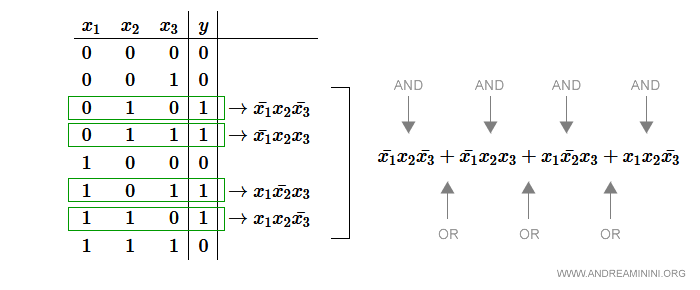
Ho così ottenuto l'espressione algebrica della tavola di verità.

Nota. Prima di disegnare il circuito, è opportuno verificare che non ci siano semplificazioni nell'espressione algebrica. Ad esempio $$ \bar{x_1}x_2\bar{x_3} + \bar{x_1}x_2x_3 + x_1\bar{x_2}x_3 + x_1x_2\bar{x_3} $$ $$ \bar{x_1}x_2 ( \bar{x_3} + x_3 ) + x_1\bar{x_2}x_3 + x_1x_2\bar{x_3} $$ $$ \bar{x_1}x_2 ( 1 ) + x_1\bar{x_2}x_3 + x_1x_2\bar{x_3} $$ $$ \bar{x_1}x_2 + x_1\bar{x_2}x_3 + x_1x_2\bar{x_3} $$ Per semplicità espositiva in questo esempio evito di farlo... ma va sempre fatto.

A questo punto mi basta disegnare i segnali x₁,x₂,x₃ in un circuito logico rappresentando le relazioni AND e OR con le relative porte logiche.

Ho così ottenuto un circuito di 4 porte AND e una porta OR.

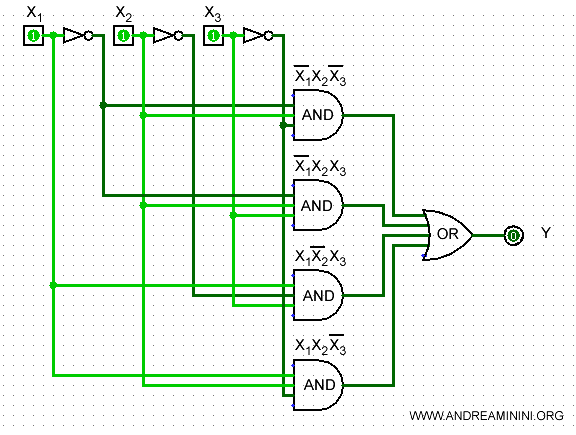
In questo modo ho disegnato il circuito logico a partire dalla tavola di verità.

Il circuito logico riflette perfettamente ogni valore della tavola.

E così via.