L'analisi degli anelli in un circuito con generatori di tensione

L'analisi degli anelli ( o mesh analysis ) è un metodo alternativo per determinare le correnti in un circuito elettrico.

Posso usarlo soltanto nei circuiti in cui i rami non si incrociano ( cd circuiti planari ).

A cosa serve?

Nella mesh analysis non prendo in considerazione gli elementi del circuito elettrico ma gli anelli.

Questo mi permette di ridurre il numero di equazioni matematiche da risolvere.

Nota. In questa pagina di appunti descrivo il funzionamento dell'analisi degli anelli in un circuito con generatori di tensione. Nel caso dei circuiti con generatori di corrente va usato un altro metodo.

Come funziona l'analisi degli anelli

I passi da seguire per analizzare un circuito con generatori di tensione tramite la mesh analysis sono i seguenti:

1. Individuo gli anelli del circuito. Un anello è una maglia del circuito che non contiene altre maglie al suo interno.
2. Assegno un'incognita (i) a ogni n-esimo anello (n)
3. Scrivo l'equazione di ogni anello con la legge di Kirchhoff (KVL)
4. Applico la legge di Ohm per esprimere le tensioni in corrente dove è necessario
5. Risolvo il sistema di n equazioni per trovare i valori delle incognite i della corrente

Un esempio pratico

In questo esercizio ho un circuito elettrico composto da due anelli.

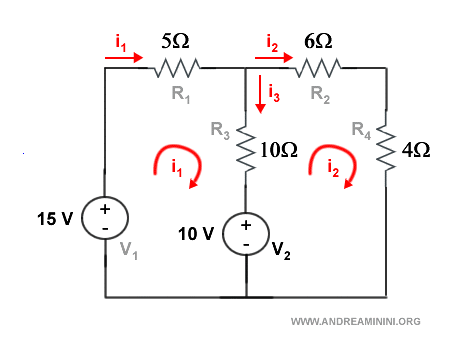
A ogni anello assegno l'incognita i₁ e i₂. Un'ulteriore incognita i₃ la assegno al ramo comune tra i due anelli.

Scelgo per convenzione il verso della corrente in senso orario.

A questo punto, scrivo le equazioni dei due anelli secondo la legge di Kirchhoff delle tensioni (KVL).

Uso soltanto le correnti degli anelli i₁ e i₂.

$$ \begin{cases} -V_1 + R_1 i_1 + R_3 (i_1 - i_2) + V_2 = 0 \\ \\ R_2 i_2 + R_4 i_2 - V_2 + R_3 (i_2 - i_1) = 0 \end{cases} $$

La prima equazione indica l'anello a sinistra, la seconda quello di destra.

Sostituisco i valori che già conosco alle incognite.

$$ \begin{cases} -15 + 5 i_1 + 10 (i_1 - i_2) + 10 = 0 \\ \\ 6 i_2 + 4 i_2 - 10 + 10 (i_2 - i_1) = 0 \end{cases} $$

Poi semplifico il sistema

$$ \begin{cases} -5 + 15 i_1 - 10 i_2 = 0 \\ \\ 20 i_2 - 10 - 10 i_1 = 0 \end{cases} $$

$$ \begin{cases} -1 + 3 i_1 - 2 i_2 = 0 \\ \\ 2 i_2 - 1 - i_1 = 0\end{cases} $$

Ora risolvo il sistema con il metodo di sostituzione.

Metto in evidenza i₁ nella seconda equazione e lo sostituisco nella prima equazione.

$$ \begin{cases} -1 + 3 (2 i_2 - 1) - 2 i_2 = 0 \\ \\ i_1 = 2 i_2 - 1 \end{cases} $$

$$ \begin{cases} -4 + 4 i_2 = 0 \\ \\ i_1 = 2 i_2 - 1 \end{cases} $$

$$ \begin{cases} i_2 = 1 \\ \\ i_1 = 2 i_2 - 1 \end{cases} $$

Ho trovato il valore della corrente i₂=1 A.

A questo punto sostituisco il valore di i₂ nella seconda equazione.

$$ \begin{cases} i_2 = 1 \\ \\ i_1 = 2 (1) - 1 \end{cases} $$

$$ \begin{cases} i_2 = 1 \\ \\ i_1 = 1 \end{cases} $$

Ho trovato il valore della corrente i₁=1 A.

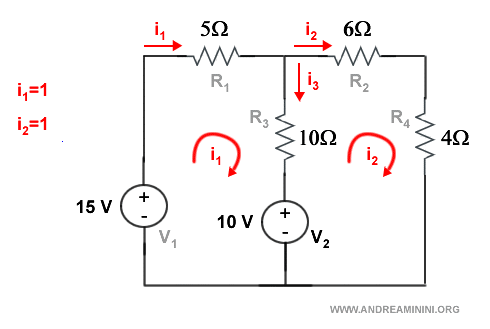
Mi manca soltanto il valore della corrente i₃ nel ramo comune tra i due anelli, dove le correnti i₁ e i₂ scorrono in verso opposto.

Per trovarlo mi basta calcolare la differenza i₁-i₂ delle correnti negli anelli che già conosco.

$$ i_3 = i_1 - i_2 $$

$$ i_3 = 1 - 1 $$

$$ i_3 = 0 $$

La corrente i₃ è uguale a 0 A.

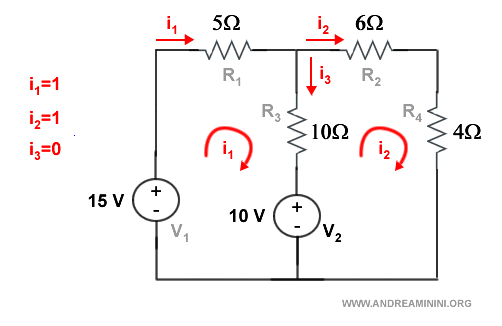
Con quest'ultimo dato ho risolto il problema con l'analisi degli anelli.

Ho trovato tutti i valori della corrente nel circuito.

E così via.