Analisi degli anelli con generatori di corrente

Quando il circuito contiene generatori di corrente dipendenti o indipendenti, l'analisi degli anelli ( mesh analysis ) va svolta in modo diverso.

• Se il generatore di corrente appartiene a un solo anello, pongo la corrente dell'anello uguale a quella del generatore di corrente.
• Se il generatore di corrente appartiene a due anelli contemporaneamente, considero il ramo in cui si trova (inclusi gli altri eventuali elementi del ramo) come un superanello a se stante. Poi applico la legge di Kirchhoff sulle tensioni (KVL) al superanello.

  Nota. Un superanello deve rispettare la legge KVL come qualsiasi anello. Tuttavia, non è possibile conoscere la tensione di un generatore di corrente a partire dalla sua corrente. Per questo motivo un superanello va elaborato in modo speciale.

  Se due superanelli si intersecano, vanno considerati come un unico super anelli

Esempio pratico

Esempio 1

Questo circuito ha un generatore di corrente nel secondo anello.

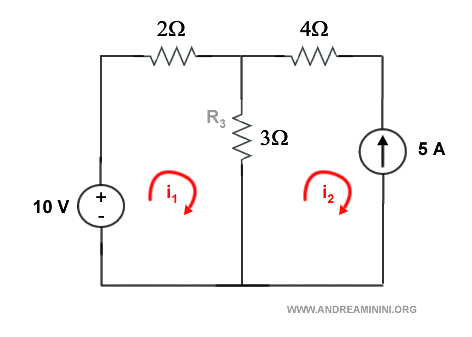
Pertanto, assegno il valore i₂=-5 all'anello del generatore di corrente.

L'altro anello i₁ lo elaboro con la legge di Kirchhoff delle correnti (KVL).

$$ \begin{cases} -10 + 2 i_1 + 3 (i_1-i_2) = 0 \\ i_2 = -5 \end{cases} $$

Sostituisco i₂=-5 nella prima equazione

$$ \begin{cases} -10 + 2 i_1 + 3 (i_1-(-5)) = 0 \\ i_2 = -5 \end{cases} $$

$$ \begin{cases} 5 i_1 + 5 = 0 \\ i_2 = -5 \end{cases} $$

$$ \begin{cases} i_1 = -1 \\ i_2 = -5 \end{cases} $$

Esempio 2

Questo circuito ha un generatore di corrente in entrambi gli anelli.

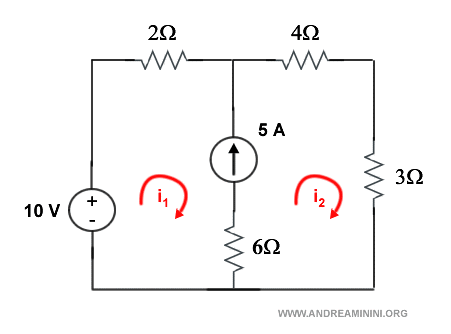
In questo caso non posso attribuire il generatore di corrente a un anello del circuito.

Lo elimino dal circuito e lo analizzo con la legge di Kirchhoff sulla corrente KCL.

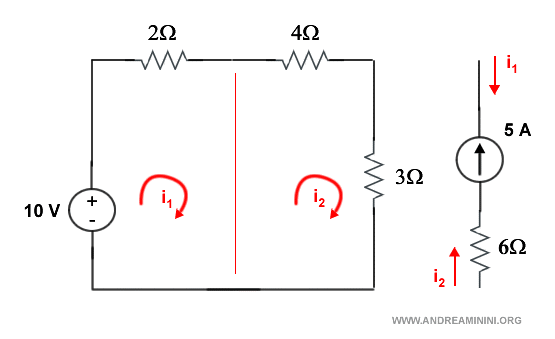
In questo modo posso trattare il primo circuito a sinistra con la KVL e il secondo circuito a destra con la KCL.

$$ \begin{cases} -10 + 2 i_1 + 4 i_2 + 3 i_2 = 0 \\ -5 + 6 (i_2-i_1) = 0 \end{cases} $$

Poi semplifico, determino i₂ nella seconda equazione e la sostituisco nella prima

$$ \begin{cases} -10 + 2 i_1 + 7 i_2 = 0 \\ -5 + 6 i_2 - 6 i_1 = 0 \end{cases} $$

$$ \begin{cases} -10 + 2 i_1 + 7 i_2 = 0 \\ i_2 = i_1 + \frac{5}{6} \end{cases} $$

$$ \begin{cases} -10 + 2 i_1 + 7 ( i_1 + \frac{5}{6} ) = 0 \\ i_2 = i_1 + \frac{5}{6} \end{cases} $$

$$ \begin{cases} -10 + 2 i_1 + 7 i_1 + \frac{55}{6} = 0 \\ i_2 = i_1 + \frac{5}{6} \end{cases} $$

$$ \begin{cases} 9 i_1 + \frac{55-60}{6} = 0 \\ i_2 = i_1 + \frac{5}{6} \end{cases} $$

$$ \begin{cases} i_1 = \frac{5}{54} \\ i_2 = i_1 + \frac{5}{6} \end{cases} $$

Una volta trovata i₁ lo sostituisco nella seconda equazione

$$ \begin{cases} i_1 = \frac{5}{54} \\ i_2 = \frac{5}{54} + \frac{5}{6} \end{cases} $$

$$ \begin{cases} i_1 = \frac{5}{54} \\ i_2 = \frac{25}{27} \end{cases} $$

$$ \begin{cases} i_1 = 0.09 A \\ i_2 = 0.92 A \end{cases} $$

Ho trovato i valori della corrente nei due anelli i₁=0.09 A e i₂=0.92 A.

Esempio 3 ( più superanelli )

Può capitare che un circuito abbia più superanelli.

Se due o più superanelli sono contigui, li posso accorpare in un unico superanello.

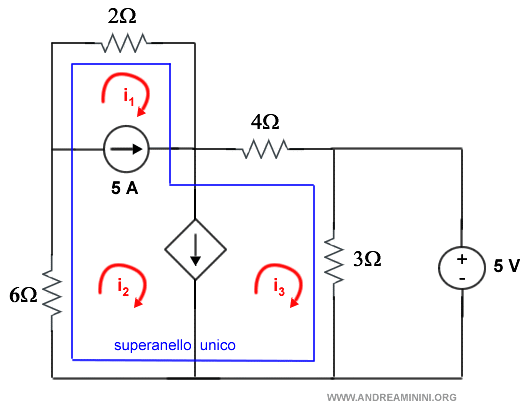
Se invece due superanelli non sono contigui, devo trattarli separatamente.

Il resto dell'analisi è identico, elimino il superanello unico dal circuito e calcolo le correnti.

 

 

E così via.