Teorema

In matematica e in logica un teorema è una proposizione che viene dimostrata a partire da alcune premesse iniziali, dette ipotesi, seguendo un ragionamento logico-deduttivo.

La dimostrazione è una sequenza di deduzioni a partire da alcune premesse considerate vere, dette ipotesi, giunge ad affermare una nuova proposizione detta tesi.

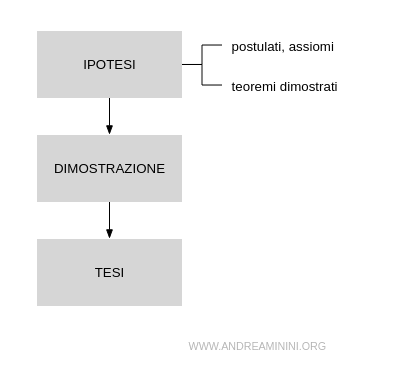
Le premesse possono essere assiomi e postulati, che sono accettati come vere senza bisogno di ulteriore dimostrazione, e/o altri teoremi già dimostrati.

A seconda della natura del teorema, le dimostrazioni possono essere molto semplici o molto complesse.

Esempio. Se un triangolo è isoscele (ipotesi) allora il triangolo ha due angolo congruenti (tesi).

Una volta che un teorema è stato dimostrato, può essere usato come punto di partenza per dimostrare ulteriori teoremi.

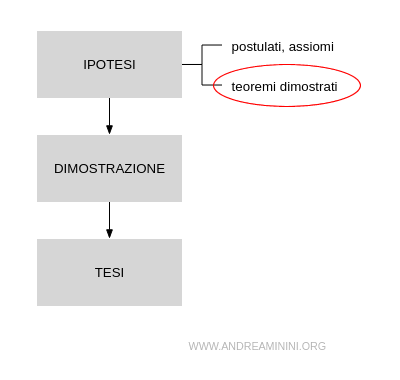
In questo modo, i matematici costruiscono una struttura logica di conoscenze che si basa su un piccolo numero di assiomi e postulati.

Si parla di corollario quando un teorema è una diretta conseguenza di un altro teorema già dimostrato.

Nota. Il termine "corollario" deriva da "corolla", ossia i petali che circondano un fiore. L'analogia è chiara. La parte centrale del fiore è il teorema mentre i petali che lo circondano sono i corollari.

Un teorema è detto teorema inverso o reciproco se scambiando tra loro l'ipotesi e la tesi ottengo la proposizione inversa.

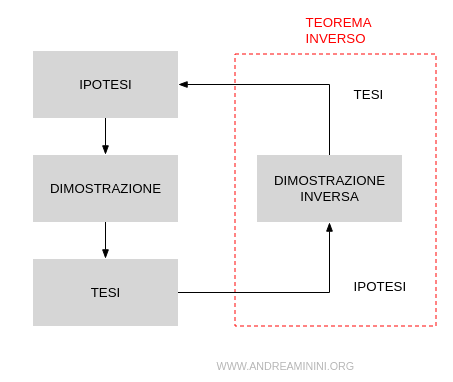
Quindi, l'inverso di un teorema afferma che se il risultato del teorema originale è vero, allora la premessa del teorema originale deve essere vera.

Esempio. Considero il teorema precedente: "Se un triangolo è isoscele (ipotesi) allora il triangolo ha due angolo congruenti (tesi)." In questo caso si può dimostrare anche il teorema inverso: "Se un triangolo ha due angoli congruenti (ipotesi) allora il triangolo è isoscele (tesi)."

Perché sono impotanti le dimostrazione?

Una dimostrazione fornisce la certezza logica su un'affermazione o una proposizione.

Quando un teorema è stato dimostrato,è vero in ogni caso, non solo in alcuni casi particolari che abbiamo controllato.

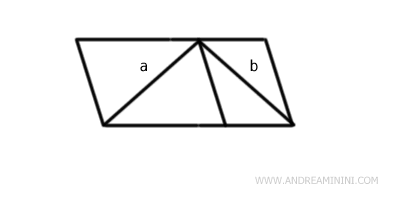
Esempio. A volte un'affermazione non dimostrata potrebbe sembrare vera all'apparenza... ma non lo è. Potrei aver osservato solo una parte di un fenomeno oppure subire un "effetto ottico". Ad esempio, questo triangolo isoscele ha i due lati "a" e "b" della stessa lunghezza.

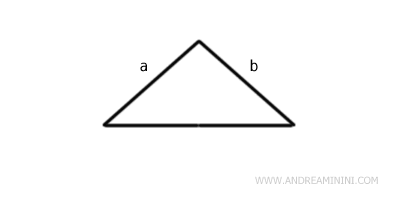
Se aggiungo al triangolo due parallelogrammi, a colpo d'occhio il lato "a" sembra diventato più lungo del lato "b", ma non è così. E' solo un effetto ottico.

Inoltre, una volta che un teorema è stato dimostrato, in matematica può essere usato come base per dimostrare altri teoremi.

Infine, le dimostrazioni sono importanti perché evitano le contraddizioni tra teoremi diversi e garantiscono la coerenza interna della matematica.

E così via.