Il quadrato magico in matematica

Cosa sono i quadrati magici

I quadrati magici sono tabelle quadrate composte da numeri interi disposti in modo da ottenere la stessa somma dei numeri di ogni riga, di ogni colonna e delle due diagonali.

La somma dei numeri è costante ed è detta costante di magia del quadrato.

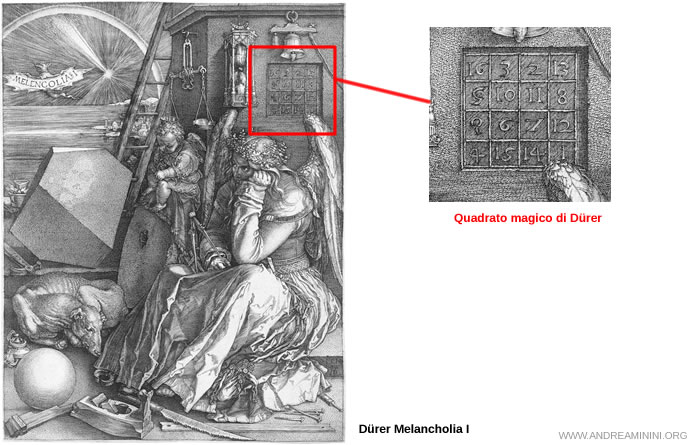
Un esempio di quadrato magico è il quadrato magico di Dürer

$$\begin{pmatrix} 16 & 3 & 2 & 13 \\ 5 & 10 & 11 & 8 \\ 9 & 6 & 7 & 12 \\ 4 & 15 & 14 & 1 \end{pmatrix}$$

Si tratta di un quadrato magico di ordine 4 perché è composto da quattro righe e quattro colonne.

La somma dei numeri di ogni riga è 34.

$$16 + 3 + 2 + 13 = 34 \\ 5 + 10 + 11 + 8 = 34 \\ 9 + 6 + 7 + 12 = 34 \\ 4 + 15 + 14 + 1 = 34$$

La somma dei numeri di ogni colonna è 34.

$$16 + 5 + 9 + 4 = 34 \\ 3 + 10 + 6 + 15 = 34 \\ 2 + 11 + 7 + 14 = 34 \\ 13 + 8 + 12 + 1 = 34$$

La somma dei numeri di entrambe le diagonali è 34.

$$16 + 10 + 7 + 1 = 34 \\ 13 + 11 + 6 + 4 = 34$$

Pertanto, la costante di magia del quadrato è 34

Nota. Si chiama quadrato di Dürer perché venne raffigurato nell'incisione Melancholia I del 1514 di Albrecht Dürer. In passato i quadrati magici erano considerati dei simboli matematici esoterici, simboli sacri o dei portafortuna.

Un altro esempio è il quadrato magico impresso sul portale della Sagrada Familia a Barcellona.

E' un quadrato magico di ordine 4 con la costante magica è uguale a 33

$$\begin{pmatrix} 1 & 14 & 14 & 4 \\ 11 & 7 & 6 & 9 \\ 8 & 10 & 10 & 5 \\ 13 & 2 & 3 & 15 \end{pmatrix}$$

I quadrati magici sono molto antichi.

Uno dei più antichi quadrati magici è il quadrato magico di Lo Shu che risale al III millennio a.C. in Cina.

$$\begin{pmatrix} 4 & 9 & 2 \\ 3 & 5 & 7 \\ 8 & 1 & 6 \end{pmatrix}$$

E' un quadrato magico di ordine 3 con costante di magia uguale a 15.

Nota. In Cina il quadrato magico era un simbolo sacro di armonia universale. Il numero 1 rappresentava l'inizio e il numero 9 la fine (ultima cifra decimale). Il numero 15 è la durata dei 24 cicli dell'anno solare cinese. Inoltre, nel quadrato i numeri e dispari si alternano simboleggiando l'alternanza tra lo yin e lo yang. Lo Shu era usato anche nella progettazione dei templi.

I quadrati magici sono generalmente composti da numeri naturali.

Tuttavia, esistono esempi pratici di quadrati magici realizzati anche con i numeri interi positivi e negativi.

Ecco un esempio di quadrato magico 3x3 composto da interi con costante magica uguale a 6

$$\begin{pmatrix} 5 & -2 & 3 \\ 0 & 2 & 4 \\ 1 & 6 & -1 \end{pmatrix}$$

La somma algebrica delle righe, delle colonne e delle due diagonali è sempre uguale a 6.

Il quadrato magico perfetto

Si parla di quadrato magico normale o perfetto quando un quadrato n x n, composto da n righe e n colonne, è composto da tutti i numeri da 1 a n².

Un quadrato magico n x n è composto da n² elementi.

Pertanto, in un quadrato magico ogni numero da 1 a n² può comparire una sola volta.

Ad esempio, il quadrato di Dürer è un quadrato perfetto perché è un quadrato 4x4 e i suoi elementi sono compresi tra 1 e 4² ossia tra 1 e 16.

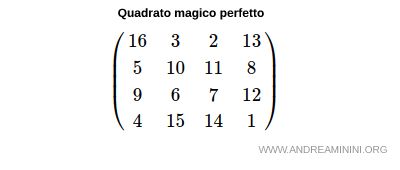
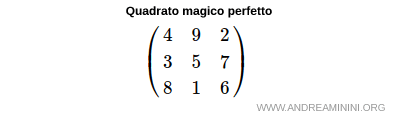
Anche il quadrato magico di Lo Shu è perfetto perché è un quadrato di ordine 3 che comprende tutti i numeri tra 1 e 9

Viceversa, il quadrato della Sagrada Familia non è un quadrato perfetto perché alcuni numeri sono ripetuti (10, 14) e altri numeri da 1 a 16 sono mancanti (12, 16).

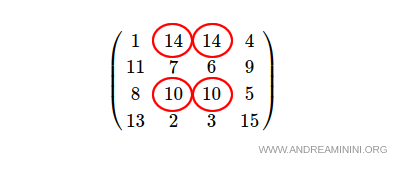
Lo gnomone

Un quadrato magico 4x4 è detto gnomone se i quadrati 2x2 che si trovano nei quattro angoli hanno la stessa somma.

Ad esempio, il quadrato nella Sagrada Familia è anche uno gnomone perché i quadrati 2x2 agli angoli (e anche il quadrato 2x2 centrale) hanno tutti la somma dei numeri uguale a 33.

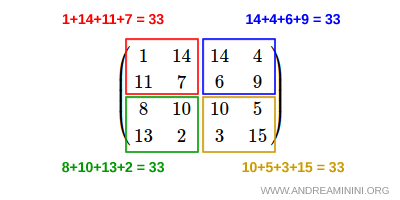
Nota. Nel quadrato della Sagrada Familia anche il quadrato 2x2 centrale (7+6+10+10) ha la somma uguale a 33 e la somma dello gnomone coincide con la costante di magica del quadrato (33).

Un altro esempio di gnomone è il quadrato magico di Dürer.

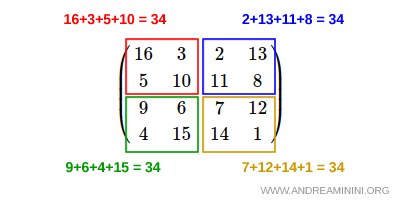
I quadrati 2x2 agli angoli hanno tutti la stessa somma (34).

E così via.