La notazione asintotica
In matematica la notazione asintotica consente di confrontare il tasso di crescita ( comportamento asintotico ) di una funzione nei confronti di un'altra.
In informatica il calcolo asintotico è utilizzato per analizzare la complessità di un algoritmo. In particolar modo, per stimare quanto aumenta il tempo al crescere della dimensione n dell'input.
Tipi di notazioni asintotiche
Esistono tre notazioni asintotiche:
- Notazione asintotica O. La notazione O grande è il limite superiore asintotico
- Notazione asintotica Ω. La notazione omega è il limite inferiore asintotico
- Notazione asintotica θ. La notazione Theta è il limite asintotico stretto
La notazione asintotica O
La notazione asintotica O è il limite superiore asintotico.
Date due funzioni f(n) e g(n), si dice che f(n)=O(g(n)) se esiste un valore c>0 tale che 0≤f(n)≤c·g(n) per ogni n≥ n0.
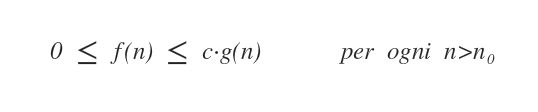
Un esempio pratico
Se analizziamo il comportamento delle funzioni nel seguente grafico, a partire da n0 la f(x) è sempre più grande di c·g(n).
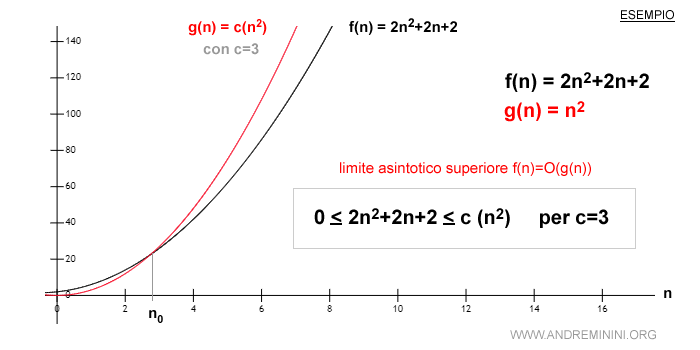
Per questa ragione la notazione asintotica O è detta limite asintotico superiore.
In tali circostanze la f(n) è una delle funzioni dell'insieme O(g(n)).
La notazione f(n)=O(g(n)) si legge f(n) è "O grande" di g(n).
Nota. Va comuque specificato che la notazione precedente f(n)=O(g(n)) è un abuso di notazione, anche se è molto diffusa nei libri di testo. Sarebbe più corretto scrivere f(n)∈O(g(n)).
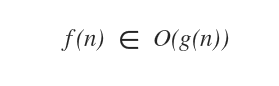
In generale una funzione a1n2+a2n+a3 è sempre O(n2) se a1>0.
La notazione asintotica omega Ω
La notazione asintotica Ω è il limite asintotico inferiore.
Date due funzioni f(n) e g(n), si dice che f(n)=Ω(g(n)) se esiste un valore c>0 tale che 0≤c·g(n)≤f(n) per ogni n≥ n0.
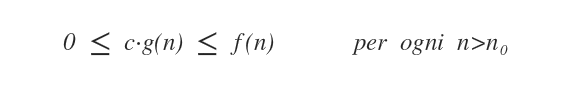
Un esempio pratico
Analizzando il comportamento delle funzioni nel seguente grafico, la f(n) è sempre più piccola di c·g(n) a partire da n0.
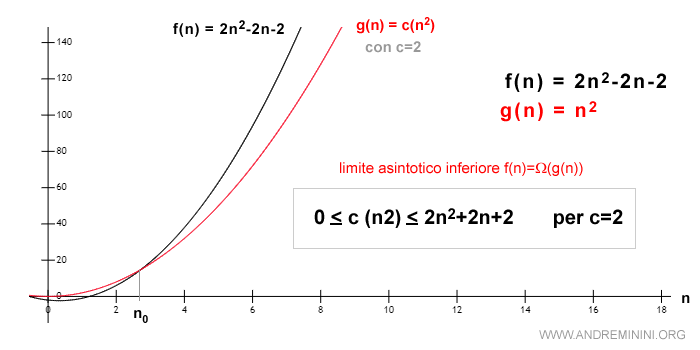
Per questo motivo la notazione asintotica omega (Ω) è detta limite asintotico inferiore.
Quindi la f(n) è una delle funzioni dell'insieme Ω(g(n)).
La notazione f(n)=Ω(g(n)) si legge f(n) è "omega" di g(n).
La notazione asintotica theta θ
La notazione asintotica θ è il limite asintotico stretto.
Date due funzioni f(n) e g(n), si dice che f(n)=θ(g(n)) se esistono due valori c1>0 e c2>0 tali che 0≤c1·g(n)≤f(n)≤c2·g(n) per ogni n≥ n0.
Un esempio pratico
Guardando il comportamento delle due funzioni nel seguente grafico, a partire da n0 la f(n) è sempre compresa tra c1·g(n) e c2·g(n).
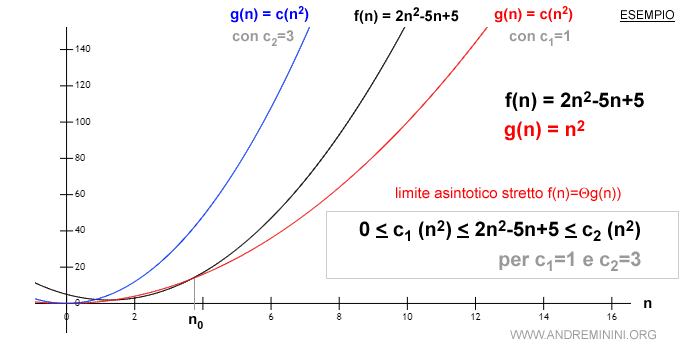
Per questo motivo la notazione asintotica theta (θ) è detta limite asintotico stretto.
Quindi la f(n) è una delle funzioni dell'insieme θ(g(n)).
La notazione f(n)=θ(g(n)) si legge f(n) è "theta" di g(n).
Nota. Se una funzione è θ(g(n)) allora è anche O(g(n)) e Ω(g(n)) perché esiste sia un limite asintotico superiore che inferiore. E viceversa, se una funzione è sia O(g(n)) che Ω(g(n) allora è anche θ(g(n).

In generale qualsiasi funzione polinomiale di grado k con coefficiente ak>0 appartiene all'insieme θ(nk).
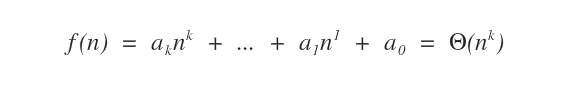
Le proprietà del limite asintotico stretto
Nel caso del limite asintotico stretto valgono le seguenti proprietà
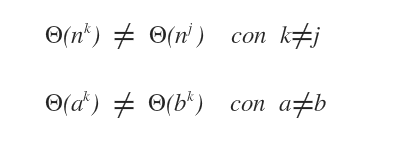
Come calcolare il limite asintotico
Per determinare i limiti asintotici di due funzioni f(n) e g(n) si utilizza il metodo del limite del rapporto f(n)/g(n).
- Se il limite del rapporto f(n)/g(n) per n→∞ è zero, allora la funzione f(n) è O(g(n)).
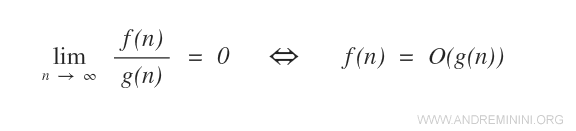
- Se il limite del rapporto f(n)/g(n) per n→∞ è infinito, allora la funzione f(n) è omega Ω(g(n)).
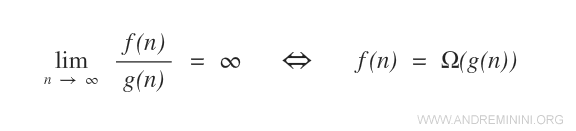
- Se il limite del rapporto f(n)/g(n) per n→∞ tende a un numero finito k, allora la funzione f(n) è theta θ(g(n)).
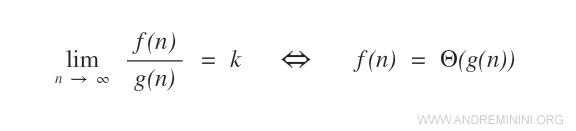
Nota. Ovviamente, il metodo del limite è utilizzabile soltanto se esiste il limite del rapporto f(n)/g(n). Se non esiste, il limite asintotico non può essere definito con questo metodo.
Le proprietà dei limiti asintotici
La proprietà della transitività
Date tre funzioni f(n), g(n), h(n).
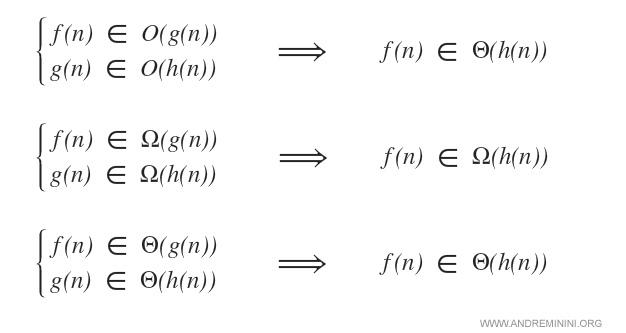
La proprietà della riflessività
Data una funzione f(n)
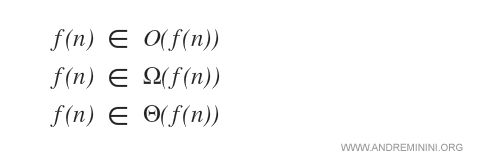
La proprietà della simmetria
Date due funzioni f(n) e g(n)
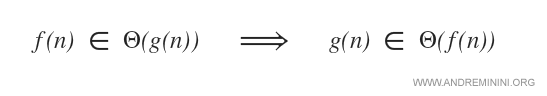
La proprietà della simmetria trasposta
Date due funzioni f(n) e g(n)
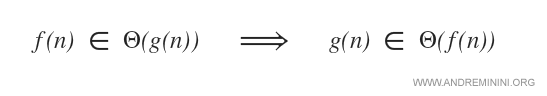
La differenza tra O grande e o piccola
Nella O grande è sufficiente che sia almeno un c>0 tale che 0≤f(n)≤cg(n) per ogni n>n0.
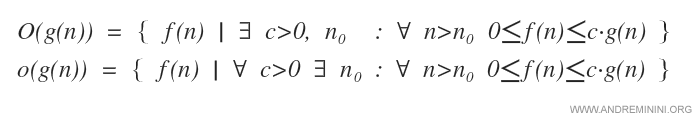
Nella o piccola, invece, per ogni c>0 esiste un n0>0 tale che 0≤f(n)≤cg(n).
Quindi, la o(g(n)) piccola implica la O(g(n)) grande.
La differenza tra omega grande (Ω) e omega piccola (ω)
Nella omega grande Ω è sufficiente che sia almeno un c>0 tale che 0≤cg(n)≤f(n) per ogni n>n0.
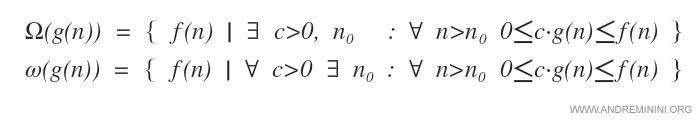
Nella omega piccola ω, invece, per ogni c>0 esiste un n0>0 tale che 0≤cg(n)≤f(n).
Quindi, la ω(g(n)) piccola implica la Ω(g(n)) grande.
