Il metodo di induzione
In matematica il metodo di dimostrazione per induzione è usato per dimostrare asserzioni sui numeri interi positivi.
A cosa serve? Consente di provare le proprietà dell'insieme o di un sottoinsieme dei numeri interi positivi.
Perché usare il metodo per induzione
Se voglio dimostrare una qualsiasi proposizione P(n), dovrei verificare la proposizione per ogni numero intero positivo da 1 a n.

Dopo aver verificato per k volte, posso soltanto affermare che la proposizione P(n) è "abbastanza plausibile".
Tuttavia, per quante verifiche possa fare non potrò mai dimostrare la validità della proprietà su tutti i numeri interi positivi, essendo un insieme infinito (n=∞).
In questi casi conviene usare il metodo per induzione. Il metodo dell'induzione mi permette di sfruttare una proprietà dei numeri interi positivi per verificare se la proposizione P(n) è vera oppure no, senza doverla ripetere per tutti i numeri.
Come funziona il metodo per induzione?
Con il metodo dell'induzione analizzo soltanto il risultato delle proposizioni P(1) e P(k+1) prendendo P(k) vera per ipotesi.
Per il teorema di induzione se P(k+1) è vera anche P(k) è vera.

Nota. Con il termine P(1) intendo il primo numero intero positivo che soddisfa la condizione della proposizione. Non necessariamente è sempre uguale a 1.
E' una sorta di effetto domino
Se P(k+1) è vera allora P(k) è vera. Lo stesso vale per tutti i numeri successivi.
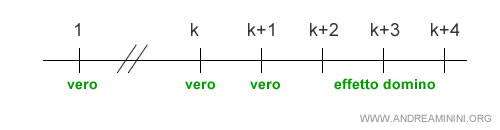
Quindi, la proposizione P(n) è vera per tutti i numeri dell'insieme preso come riferimento.
Nota. Questo metodo consente di dimostrare le asserzioni sui numeri interi positivi. Non è valido, invece, per i numeri reali.
Il teorema di induzione ( o principio di induzione )
Secondo il teorema di induzione
Secondo il principio di induzione se P è una proprietà che vale per P(1) e se P(k)⇒P(k+1) per ogni k, allora P(n) vale per ogni n. Dove k e n sono numeri naturali.
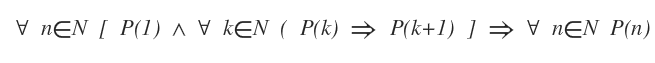
Dimostrazione
Le due condizioni di induzione consentono di affermare che si tratta di un insieme induttivo.
Cos'è un insieme induttivo? Dato un insieme A di numeri reali, diciamo che A è un insieme induttivo se soddisfa le seguenti proprietà:
1) Il numero 1 appartiene ad A
2) Se x appartiene ad A allora x+1 appartiene ad A
Per definizione ogni numero intero positivo appartiene a tutti gli insiemi induttivi.
Pertanto, ogni intero positivo appartiene anche ad A.
Come si applica il metodo di induzione
Una qualsiasi proposizione P(n) è vera se sono soddisfatte queste condizioni:
- P(1) è vera
- Sia k un numero intero arbitrario maggiore o uguale a 1, se P(k) è vera allora è vera anche P(k+1).
La procedura spiegata praticamente
Ho una proposizione P(n) ma non so se sia vera o falsa.
Per scoprirlo applico il teorema di induzione.
- verifico se la proprietà P(n) è vera per n=1 ossia provo la veridicità di P(1)
( base induttiva ) - poi suppongo per ipotesi che la proprietà P(n) è vera anche per n=k
( ipotesi induttiva ) - da questa ipotesi deduco e verifico se P(n) è vera anche per n=k+1
( passo induttivo )
Secondo il principio di induzione, questo consente di affermare che la proprietà P(n) è vera per ogni numero intero positivo ( ∀ n∈N ).
Un esempio pratico di induzione
Dimostrare che per ogni n≥1 la proposizione P(n) è divisibile per 6
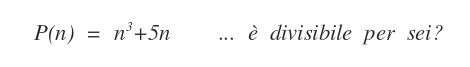
Per n=1 la proposizione P(n) è vera. E' divisibile per 6.
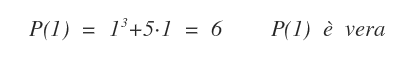
Per ipotesi affermo che la proposizione P(k) è vera per n=k.
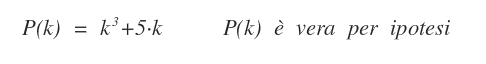
Quindi verifico se è vera per n=k+1.
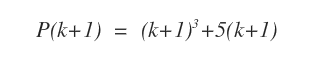
Svolgo i calcoli della proposizione P(k+1) per trovare le componenti che formano la proposizione di P(k).
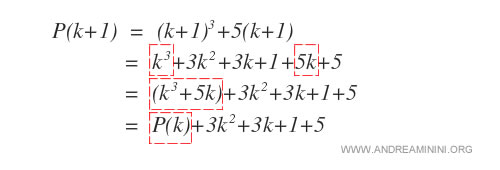
A questo punto svolgo gli altri calcoli per semplificare la proposizione P(k+1).
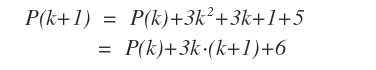
Sapendo che:
- P(k) è per ipotesi divisibile per 6
- 3k(k+1) è divisibile per sei in quanto almeno uno tra k e k+1 è un numero pari
Nota. In alternativa, si può affermare che k(k+1) è sicuramente un numero pari essendo il prodotto di un numero dispari per uno pari. Pertanto k(k+1) è divisibile per 2. Essendo moltiplicato per 3 è anche divisibile per 3. Quindi sono soddisfatte tutte le condizioni di divisibilità di un numero per 6.
- Il numero +6 è ovviamente divisibile per 6
Se tutte le componenti di P(k+1) sono divisibili per 6, anche P(k+1) è divisibile per 6.
Pertanto, P(k+1) è vera.
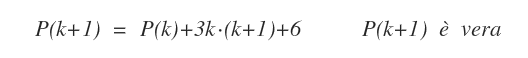
In conclusione, in base al principio di induzione posso affermare che P(n) è divisibile per 6 per ogni n≥1.
